РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ ПО СТАТИСТИКЕ
Тема 1. Сводка и группировка
Пример 1.
Численность осужденных в регионе распределяется по возрастам следующим образом:
| Возраст, лет | Количество осужденных |
| 14 - 17 | |
| 18 – 24 | |
| 25 – 29 | |
| 30- 49 | |
| 50 и старше |
Определить, в какой возрастной группе численность осужденных на 1000 человек была больше, если распределение населения региона по возрастным группам следующее:
| Возраст, лет | Численность населения, тыс. чел. |
| 0 – 9 | 429,4 |
| 10 – 19 | 405,5 |
| 20 – 29 | 377,2 |
| 30 – 39 | 476,4 |
| 40 – 49 | 290,3 |
| 50 – 59 | 337,9 |
| 60 – 69 | 267,0 |
| 70 и старше | 164,0 |
Решение
Для приведения данных в сопоставимый вид необходимо выполнить группировку (методом долевой перегруппировки и укрупнения интервалов) распределения населения региона по возрастным группам, образуя новые группы со следующими интервалами: 0 – 13, 14 – 17, 18 – 24, 25 – 29, 30 – 49, 50 и старше.
В первую новую группу [0 – 13] войдет полностью первая возрастная группа населения и часть второй группы из таблицы. От интервала второй группы нужно взять 4 части. Величина интервала этой группы составляет 10. Следовательно, нужно взять от нее 4/10 (4:10). Такую же часть во вновь образуемую первую группу надо взять и от численности, т.е. 405,5 × (4:10)= 162,2 тыс. чел. Тогда и в новой первой группе численность населения будет: 429,4 + 162,2 = 591,6 тыс. чел.
Вторую новую группу [14 – 17] образует часть населения второй возрастной группы [10 – 19] из таблицы: 405,5 × (4:10)= 162,2 тыс. чел.
Во вновь образованную третью группу [18 – 24] войдет часть населения второй группы [10 – 19] и часть третьей группы [20 – 29] из таблицы:
405,5 × (2:10) + 377 × (5:10)= 269,6 тыс. чел.
Все остальные группы определяются аналогично.
В результате перегруппировки получим:
| Возраст, лет | Численность населения, тыс. чел. |
| 0 – 13 | 429,4 + 405,5 × (4:10) = 591,6 |
| 14 – 17 | 405,5 × (4:10) = 162,2 |
| 18 – 24 | 405,5 × (2:10) + 377,2 × (4:10) = 269,6 |
| 25 – 29 | 377,2 × (5:10) = 188,6 |
| 30 – 49 | 476,4 + 290,3 = 766,7 |
| 50 и старше | 337,9 + 267,0 + 164,0 = 768,9 |
Используя группировку осужденных и вторичную группировку распределения населения по возрасту, рассчитаем численность осужденных на 1000 человек населения в виде относительной величины интенсивности:
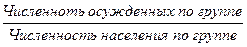 .
.
Для возраста [14 – 17]: (1,959/162,2) × 1000 = 12,1 чел. на 1000 чел.
Для возраста [18 – 24]: (2,673/269,6) × 1000 = 9,9 чел. на 1000 чел. и т.д.
Результаты представим в табличном виде:
| Возраст, лет | Численность осужденных на 1000 чел. населения |
| 14 - 17 | 12,1 |
| 18 – 24 | 9,9 |
| 25 – 29 | 11,6 |
| 30- 49 | 5,9 |
| 50 и старше | 0,8 |
Итак, больше всего осужденных на 1000 человек населения было в возрастной группе 14 – 17 лет.
Тема 2. Статистические величины
Пример 2.
Крестьянские хозяйства подразделяются по размерам земельных угодий следующим образом:
| Земельные угодья, га | Число хозяйств, ед. |
| До 3 | |
| 4 – 5 | |
| 6 – 10 | |
| 11 – 20 | |
| 21 – 50 | |
| 51 – 70 | |
| 71 – 100 | |
| 101 – 200 | |
| 201 и больше |
Рассчитать:
1) средний размер земельных угодий;
2) показатели вариации: размах, среднее линейное отклонение, среднее квадратическое отклонения, коэффициент вариации; оценить количественную однородность совокупности;
3) моду и медиану.
Решение
Для расчета требуемых показателей следует перейти от вариационного ряда к дискретному. Для этого находится середина каждого интервала. Расчет показателей выполним в табличном виде:
| Земель-ные угодья, га | Число хо-зяйств, ед. |
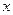
|
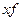
|
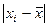
|
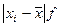
|
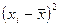
|
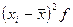
| Нако- плен-ные час-тоты | Плот-ность
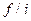
|
| До 3 | 2,5 | 57,4 | 3294,76 | 98842,8 | |||||
| 4 – 5 | 4,5 | 55,4 | 3069,16 | 153458,0 | |||||
| 6 – 10 | 51,9 | 2693,61 | 1077444,0 | ||||||
| 11 – 20 | 15,5 | 44,4 | 1971,36 | 1577088,0 | |||||
| 21 – 50 | 35,5 | 24,4 | 595,36 | 1071648,0 | |||||
| 51 – 70 | 60,5 | 0,6 | 0,36 | 216,0 | |||||
| 71 – 100 | 85,5 | 25,6 | 655,36 | 458752,0 | 23,3 | ||||
| 101 – 200 | 150,5 | 90,6 | 8208,36 | 5745852,0 | |||||
| 201 и больше | 250,5 | 190,6 | 36328,36 | 4359403,2 | 1,2 | ||||
| Итого | ∑=311360 | ∑=209264 | ∑=14542704 |
1. Средний размер земельных угодий на одно крестьянское хозяйство определяется по формуле:
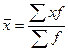 ,
,
где 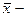 среднее значение признак;
среднее значение признак; 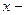 серединное значение интервала, в котором изменяется варианта (значение) усредняемого признака;
серединное значение интервала, в котором изменяется варианта (значение) усредняемого признака; 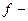 частота, с которой встречается данное значение усредняемого признака.
частота, с которой встречается данное значение усредняемого признака.
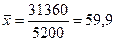 (га).
(га).
2. К показателям вариации относятся:
а) размах вариации:
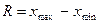 ,
,
где 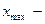 максимальное значение признака (максимальное серединное значение интервала),
максимальное значение признака (максимальное серединное значение интервала), 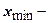 минимальное значение признака;
минимальное значение признака;
б) среднее линейное отклонение:
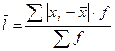 ;
;
в) среднее квадратическое отклонение:
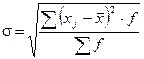 ;
;
г) коэффициент вариации:
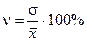 .
.
Рассчитаем указанные показатели вариации.
Размах вариации:
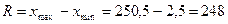 (га).
(га).
Среднее линейное отклонение:
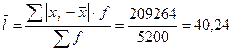 (га).
(га).
Среднее квадратическое отклонение:
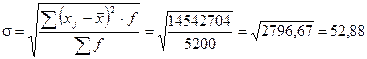 (га).
(га).
Коэффициент вариации:
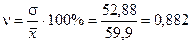 (88,2 %).
(88,2 %).
Крестьянские угодья количественно неоднородны по размеру земельных угодий.
3. Мода и медиана относятся к особому виду средних величин – структурным средним.
Мода – это наиболее часто встречаемое значение признака.
Медиана – величина признака у единицы, находящейся в середине упорядоченного ряда.
В интервальных рядах распределения структурные средние рассчитываются по особым формулам.
При расчете моды можно применить следующую формулу:
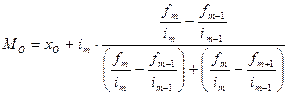 .
.
Здесь 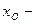 начало модального интервала, модальный интервал – интервал, в котором достигает максимума величина
начало модального интервала, модальный интервал – интервал, в котором достигает максимума величина 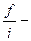 отношение частоты интервала к его величине;
отношение частоты интервала к его величине; 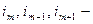 величина соответственно модального, до- и послемодального интервалов;
величина соответственно модального, до- и послемодального интервалов; 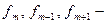 частота до- и послемодального интервалов соответственно.
частота до- и послемодального интервалов соответственно.
Примечание
В случае равных интервалов формула моды примет привычный вид:
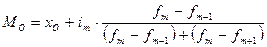 .
.
Медиана рассчитывается по формуле:
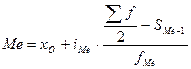 ,
,
где 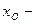 нижняя граница медианного интервала;
нижняя граница медианного интервала; 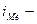 величина медианного интервала;
величина медианного интервала; 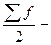 половина от общего числа наблюдений;
половина от общего числа наблюдений; 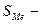 сумма накопленных частот до начала медианного интервала;
сумма накопленных частот до начала медианного интервала; 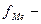 частота медианного интервала.
частота медианного интервала.
Рассчитаем структурные средние:
А. Определяем модальный интервал, в данном примере их два: [6 – 10] и [11 – 20]. Для расчета моды подставим в формулу все переменные:
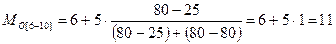 (га).
(га).
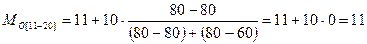 (га).
(га).
Следовательно, наиболее часто встречаемый размер земельных угодий – 11 га.
Б. Для расчета медианы определяем медианный интервал – это тот интервал, в котором находится 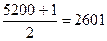 крестьянское хозяйство. В данном примере – интервал [21 – 50].
крестьянское хозяйство. В данном примере – интервал [21 – 50].
Подставляем в формулу значения:
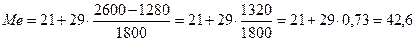 (га).
(га).
Следовательно, 50 % крестьянских хозяйств имеют размер земельных угодий меньше 42,6 га, а остальные 50 % – больше.
Тема 3. Выборочное наблюдение
Пример 3.
Определить с вероятностью 0,954 границы изменения среднего значения признака в генеральной совокупности, если известно следующее ее распределение, основанное на результатах повторного выборочного обследования:
| Группировка значений признака | Число единиц выборочной совокупности, входящих в данный интервал |
| До 4 | |
| 4 – 8 | |
| 8 – 12 | |
| 12 – 16 | |
| 16 – 20 | |
| Итого: 100 |
Решение
Среднее значение признака в генеральной совокупности находится в интервале:
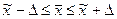 ,
,
где 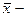 среднее значение признака в генеральной совокупности,
среднее значение признака в генеральной совокупности, 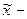 среднее значение признака в выборочной совокупности,
среднее значение признака в выборочной совокупности, 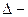 предельная ошибка выборочной средней.
предельная ошибка выборочной средней.
Для повторного отбора:
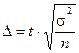 ,
,
где 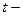 коэффициент доверия,
коэффициент доверия, 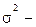 дисперсия признака в выборочной совокупности,
дисперсия признака в выборочной совокупности, 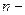 объем выборки.
объем выборки.
Определяем 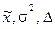 .
.
1. Среднее значение признака по выборке:
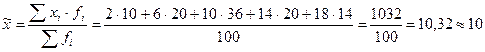 .
.
2. Выборочная дисперсия:
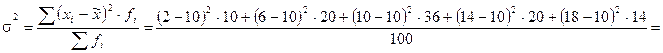
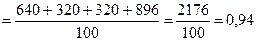 .
.
Имеем:
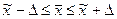 ,
, 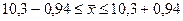 и окончательно
и окончательно 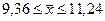 .
.
Таким образом, с вероятностью 0,954 можно предположить, что среднее значение признака в генеральной совокупности будет находиться в пределах от 9,36 до 11,24.
Пример 4.
Партия роз (80000 шт.), поступивших из Голландии, была подвергнута выбраковке. Для этого было обследовано 800 роз, отобранных при помощи механического способа отбора. Среди обследованных обнаружено 160 бракованных.
Определить с вероятностью 0,997 возможный размер убытка от некачественной транспортировки, если цена приобретения розы 10 руб.
Решение
Чтобы узнать возможный размер убытка, определим процент брака во всей партии.
Доля бракованных роз:
Ωбрака = 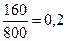 .
.
Предельная ошибка доли при повторном отборе определяется соотношением:
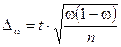 ,
,
где 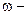 выборочная доля,
выборочная доля, 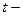 коэффициент доверия,
коэффициент доверия, 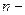 объем выборки. Подстановка числовых значений в формулу дает:
объем выборки. Подстановка числовых значений в формулу дает:
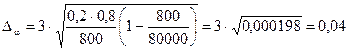 .
.
Пределы доли бракованных роз и убытков соответственно равны:
Pбрака = 0,2 ± 0,04; 0,16 ≤ Pбрака ≤ 0,24.
Возможный размер убытка (У) находится в пределах:
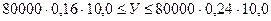
 или 128,0 тыс. руб. ≤ У ≤ 192,0 тыс. руб.
или 128,0 тыс. руб. ≤ У ≤ 192,0 тыс. руб.
Тема 4. Ряды динамики
Пример 5.
По данным о числе казненных и помилованных заключенных рассчитать по каждому ряду в отдельности абсолютные (цепные и базисные) и средние показатели динамики. Результаты расчетов представить в табличном виде.
| Год | Количество казней | Помиловано |
Решение
Рассчитаем все показатели по ряду динамики, характеризующему число казненных:
1) абсолютный прирост:
Δцеп = 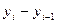 ,
,
где Δцеп – цепной абсолютный прирост значений признака (прирост по сравнению с предыдущим моментом (периодом) времени); 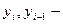 значение уровня ряда в момент (период) времени
значение уровня ряда в момент (период) времени 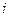 и
и 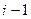 соответственно;
соответственно;
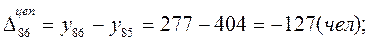
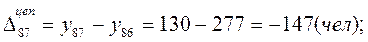
Δбаз = 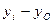 ,
,
где Δбаз – базисный абсолютный прирост значений признака (прирост по сравнению с моментом (периодом) времени, принятым за базу); 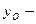 значение уровня ряда в момент (период) времени, принятый за базу сравнения
значение уровня ряда в момент (период) времени, принятый за базу сравнения
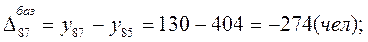
2) темп роста:
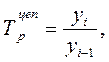
где Т 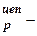 цепной темп роста (темп роста по сравнению с предыдущим моментом времени).
цепной темп роста (темп роста по сравнению с предыдущим моментом времени).
Т 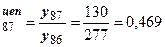 (46,9 %);
(46,9 %);
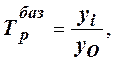
где Т 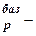 базисный темп роста (темп роста по сравнению с моментом времени, принятым за базу сравнения).
базисный темп роста (темп роста по сравнению с моментом времени, принятым за базу сравнения).
Т 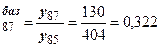 (32,2 %);
(32,2 %);
3) темп прироста:
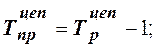
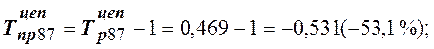
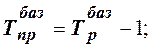
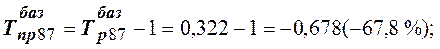
4) абсолютное значение 1 % прироста:
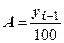 ;
;
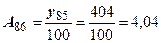 ;
;
Расчетная таблица
| Год | Число казней | Абсолютный прирост (Δ) | Темп роста, Тр, % | Темп прироста, Тпр, % | Абсолют- ное значе- ние 1 % прироста | |||
| цеп. | баз. | цеп. | баз. | цеп. | баз. | |||
| – | – | 100,0 | 100,0 | 0,0 | 0,0 | – | ||
| –127 | –127 | 68,6 | 68,6 | –31,4 | –31,4 | 4,04 | ||
| –147 | –274 | 46,9 | 32,2 | –53,1 | –67,8 | 2,77 | ||
| –112 | –316 | 67,7 | 21,8 | –32,3 | –78,2 | 1,30 | ||
| –12 | –328 | 86,4 | 18,8 | –13,6 | –81,2 | 0.88 | ||
| –4 | –332 | 94,7 | 17,8 | –5,3 | –82,2 | 0,76 | ||
| –57 | –389 | 20,8 | 3,7 | –79,2 | –96,3 | 0,72 | ||
| –14 | –403 | 6,7 | 0,2 | –93,3 | –99,8 | 0,15 | ||
| –400 | 400,0 | 1,0 | 300,0 | –99,0 | 0,01 | |||
| –385 | 475,0 | 4,7 | 375,0 | –95,3 | 0,04 | |||
| –318 | 452,0 | 21,3 | 352,6 | –78,7 | 0,19 | |||
| –33 | –351 | 61,6 | 13,1 | 38,4 | –86,9 | 0,86 | ||
| В сред- нем | –32 | –32 | 83,3 | 83,3 | –16,7 | –16,7 | – |
5) средние показатели:
а) средний уровень:
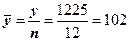 ;
;
б) средний абсолютный прирост:
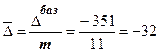 ;
;
в) средний темп роста:
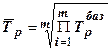 ,
,
где 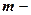 число базисных темпов роста;
число базисных темпов роста;
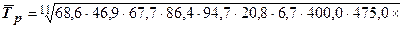
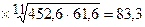 .
.
Пример 6.
Официальный курс рубля к американскому доллару и объем продаж валюты на торгах ММВБ в 1996 г. представлен в таблице:
| Дата | Курс американского доллара, руб. за 1 $ | Объем продаж, $ |
| 02.07 | 15 103 | |
| 03.07 | 21 087 | |
| 05.07 | 24 819 | |
| 09.07 | 28 369 | |
| 10.07 | 11 099 | |
| 11.07 | 13 869 | |
| 12.07 | 11 530 | |
| 16.07 | 12 316 | |
| 17.07 | 28 933 | |
| 18.07 | 16 306 | |
| 19.07 | ||
| 20.07 | ||
| 23.07 | 17 785 | |
| 24.07 | 13 976 | |
| 25.07 | 35 545 | |
| 26.07 | 22 036 | |
| 27.07 | 35 522 | |
| 30.07 | 32 717 | |
| 31.07 |
Требуется:
1) Рассчитать уравнение регрессии и оценить его надежность.
2) На основе рассчитанного уравнения регрессии определить:
а) на сколько увеличится или уменьшится объем продаж при росте курса на 1 пункт;
б) какой рынок («продавца» или «покупателя») сложился за анализируемый промежуток времени?
Решение
Поэтапно выполняются следующие действия:
1. Исключение авторегрессии.
Необходимо от исходных рядов динамики перейти к новым, построенным, например, по первым разностям:
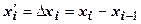 ;
;
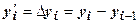 .
.
Полученные первые разности вместе с исходными данными представим в расчетной таблице 1.
Расчетная таблица 1
| Дата | Курс американского доллара, руб. за 1 $ | Объем продаж, $ | ||
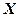
| 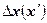
| 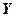
| 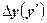
| |
| 02.07 | ― | 15 103 | ― | |
| 03.07 | 21 087 | |||
| 05.07 | 24 819 | |||
| 09.07 | 28 369 | |||
| 10.07 | 11 099 | –17270 | ||
| 11.07 | 13 869 | |||
| 12.07 | –2 | 11 530 | –2339 | |
| 16.07 | 12 316 | |||
| 17.07 | 28 933 | |||
| 18.07 | 16 306 | –12627 | ||
| 19.07 | –10448 | |||
| 20.07 | ||||
| 23.07 | 17 785 | |||
| 24.07 | 13 976 | –3809 | ||
| 25.07 | 35 545 | |||
| 26.07 | 22 036 | –13509 | ||
| 27.07 | 35 522 | |||
| 30.07 | 32 717 | –2805 | ||
| 31.07 | – 24845 |
2. По новым уровням ( 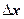 и
и 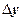 ) строится уравнение регрессии:
) строится уравнение регрессии:
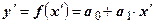 .
.
Параметры уравнения регрессии рассчитываются по следующим формулам:
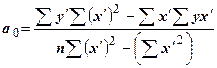 ;
;
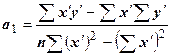 .
.
Результаты вычислений представим в расчетной таблице 2.
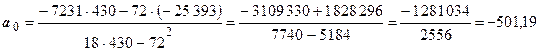 ;
;
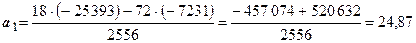 ;
;
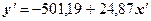 .
.
Полученные параметры можно охарактеризовать следующим образом:
параметр 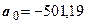 показывает, что средний абсолютный прирост объема продаж до июля 1996 г. составлял –501,19 доллара;
показывает, что средний абсолютный прирост объема продаж до июля 1996 г. составлял –501,19 доллара;
параметр 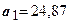 , называемый силой связи, показывает, что при росте курса на 1 пункт отрицательный прирост объема продаж уменьшится на 24,87 доллара.
, называемый силой связи, показывает, что при росте курса на 1 пункт отрицательный прирост объема продаж уменьшится на 24,87 доллара.
3. Оценим уравнение регрессии на надежность по критерию Фишера:
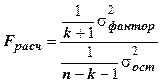 ,
,
где 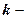 число параметров функции, описывающей тенденцию;
число параметров функции, описывающей тенденцию; 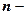 число уровней ряда;
число уровней ряда; 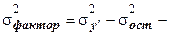 факторная дисперсия;
факторная дисперсия; 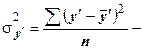 общая дисперсия;
общая дисперсия; 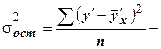 остаточная дисперсия.
остаточная дисперсия.
Расчетная таблица 2
| Дата | 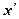
| 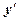
| 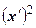
| 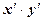
| 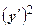
| 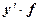
|
| 02.07 | ― | ― | ― | ― | ― | ― |
| 03.07 | 29 920 | 35 808 256 | –376,84 | |||
| 05.07 | 13 927 824 | –476,32 | ||||
| 09.07 | 14 200 | 12 602 500 | –401,71 | |||
| 10.07 | –17270 | –34 540 | 298 252 900 | –451,45 | ||
| 11.07 | 7 672 900 | –451,45 | ||||
| 12.07 | –2 | –2339 | 5 470 921 | –550,93 | ||
| 16.07 | 617 796 | –401,71 | ||||
| 17.07 | 16 617 | 276 124 689 | –476,32 | |||
| 18.07 | –12627 | –50 508 | 159 441 129 | –401,71 | ||
| 19.07 | –10448 | –104 480 | 109 160 704 | –252,49 | ||
| 20.07 | 1 194 649 | –351,97 | ||||
| 23.07 | 97 506 | 117 375 556 | –277,36 | |||
| 24.07 | –3809 | –15 236 | 14 508 481 | –401,71 | ||
| 25.07 | 129 414 | 465 221 761 | –351,97 | |||
| 26.07 | –13509 | –67 545 | 182 493 081 | –376,84 | ||
| 27.07 | 26 972 | 182 872 196 | –451,45 | |||
| 30.07 | –2805 | –16 830 | 7 868 025 | –351,97 | ||
| 31.07 | – 24845 | –74 535 | 617 274 025 | –426,58 | ||
| Итого | – 7231 | –25 393 | 2 506 887 393 | –7230,78 |
Подставляя числовые данные в формулы, получим:
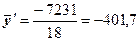 ;
;
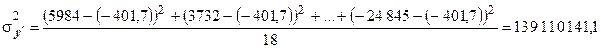 ;
;
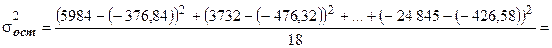
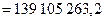 ;
;
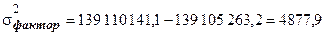 ;
;
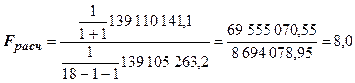 ;
;
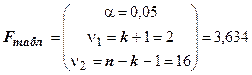 .
.
Так как 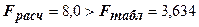 , то уравнение регрессии значимо, т.е. построенное уравнение связи адекватно отражает сложившуюся зависимость.
, то уравнение регрессии значимо, т.е. построенное уравнение связи адекватно отражает сложившуюся зависимость.
4. Для характеристики рынка, сложившегося на торгах в июле, необходимо рассчитать коэффициент корреляции между курсом американского доллара и объемом продаж:
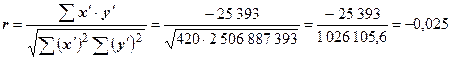 .
.
Так как коэффициент корреляции отрицательный, то можно сделать вывод, что в июле на торгах ММВБ сложился рынок «покупателя».
Тема 5. Индексы
Пример 7.
Данные о продаже товаров на рынке представлены в следующей таблице:
| Товар | Продано, тыс. кг | Цена за 1 кг, руб. | ||
| Июнь | Июль | Июнь | Июль | |
| Яблоки | 9,50 | 12,00 | ||
| Морковь | 18,00 | 15,00 |
Определить:
1) индивидуальные индексы цен и объема проданного товара;
2) общий индекс товарооборота;
3) общий индекс физического объема товарооборота;
4) общий индекс цен;
5) прирост товарооборота – всего, в том числе изменения цен и объема продажи товаров.
Показать связь между исчисленными индексами.
Решение
1. Индивидуальные индексы равны:
а) цен ― 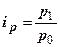 ; б) количества проданных товаров ―
; б) количества проданных товаров ― 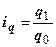 .
.
Так, для яблок 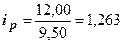 (126,3 %), т.е. цена на яблоки увеличилась на 26,3 %.
(126,3 %), т.е. цена на яблоки увеличилась на 26,3 %.
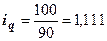 (111,1 %), т.е. количество проданных яблок увеличилось на 11,1 %.
(111,1 %), т.е. количество проданных яблок увеличилось на 11,1 %.
Соответствующие индексы для моркови равны:
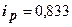 (83,3 %) и
(83,3 %) и 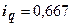 (66,7 %.
(66,7 %.
2. Общий индекс товарооборота вычисляется по формуле:
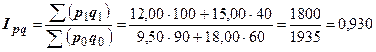 (93,0 %).
(93,0 %).
Следовательно, товарооборот в июле снизился на 7 % по сравнению с июнем.
3. Общий индекс физического объема товарооборота (количества проданных товаров) вычисляется по формуле:
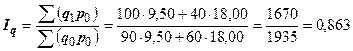 (86,3 %).
(86,3 %).
Значит, количество проданных товаров в июле было меньше на 13,7 %, чем в июне.
4. Общий индекс цен равен:
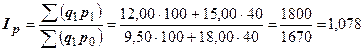 (107,8 %),
(107,8 %),
т.е. цены на оба товара в среднем выросли на 7,8 %.
5. Прирост или снижение товарооборота вычисляется как разница между числителем и знаменателем индекса товарооборота:
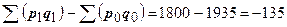 (тыс. руб.).
(тыс. руб.).
Это снижение обусловлено изменением цен на товары и изменением количества проданных товаров.
Прирост за счет изменения цен составил:
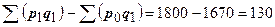 (тыс. руб.),
(тыс. руб.),
снижение за счет изменения количества проданных товаров:
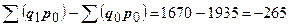 (тыс. руб.).
(тыс. руб.).
Следовательно, снижение товарооборота на 135 тыс. руб. произошло за счет сокращения количества проданных товаров на 265 тыс. руб. и за счет роста цен на 130 тыс. руб. [(-265)+(+130) = –135 тыс. руб.].
Между исчисленными индексами существует связь:
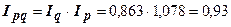 .
.
Пример 8.
Имеются следующие данные о выпуске продукции А по двум заводам района:
| Завод | Предыдущий период | Отчетный период | ||||
| Произведено продукции, тыс. шт. | Себестоимость единицы продукции, тыс. руб. | Удельный вес продукции завода | Произведено продукции, тыс. шт. | Себестоимость единицы продукции, тыс. руб. | Удельный вес продукции завода | |
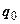
| 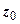
| 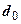
| 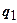
| 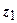
| 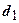
| |
| 0,50 | 0,40 | |||||
| 0,50 | 0,60 | |||||
| Итого | ― | 1,00 | ― | 1,00 |
Определить индексы себестоимости продукции:
1) переменного состава;
2) фиксированного состава;
3) влияния структурных сдвигов.
Решение
1. Определим индекс себестоимости переменного состава, который равен соотношению средней себестоимости продукции по двум заводам:
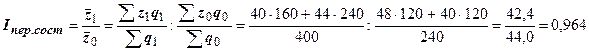 ,
,
т.е. 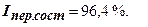
Индекс показывает, что средняя себестоимость изделия по двум заводам снизилась на 3,6 %. Это снижение обусловлено изменением себестоимости продукции по каждому заводу и изменением структуры удельного веса продукции заводов. Выявим влияние каждого из этих факторов на динамику средней себестоимости, исчислив индексы себестоимости фиксированного состава и влияния структурных сдвигов.
2) Индекс себестоимости фиксированного состава:
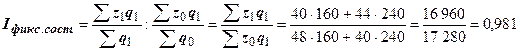 (98,1 %).
(98,1 %).
Себестоимость продукции по двум заводам в среднем снизилась на 1,9 %.
3) Индекс влияния структурных сдвигов:
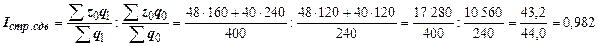 ,
,
т.е. 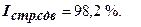
Средняя себестоимость изделия в отчетном периоде снизилась дополнительно на 1,8 % за счет изменения структуры, т.е. за счет роста удельного веса продукции завода 2 с 50 % до 60 % (здесь уровень себестоимости был ниже по сравнению с заводом 1).
Исчисленные выше индексы можно вычислить по удельным весам продукции заводов, выраженным в коэффициентах:
а) 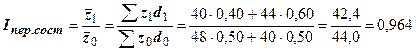 ;
;
б) 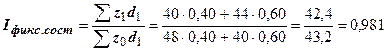 ;
;
в) 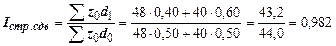 .
.
Связь между вычисленными индексами:
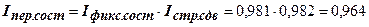 .
.
Тема 6. Анализ структуры и структурных изменений
Пример 9.
По одному из предприятий пищевой промышленности имеются данные о составе затрат на производство продукции (тыс. руб.):
| Статьи затрат | Фактический выпуск товарной продукции в оценке по себестоимости | |
| квартального плана | фактический | |
| Сырье и материалы | 257 000 | 253 000 |
| Топливо и энергия всех видов на технологические цели | ||
| Затраты на оплату труда | 75 600 | 72 400 |
| Потери от брака | ||
| Расходы по содержанию и эксплуатации оборудования | 31 000 | 39 000 |
| Общепроизводственные расходы | 84 000 | 90 000 |
| Общехозяйственные расходы | 72 000 | 73 000 |
| Производственная себестоимость | 524 800 | 538 400 |
Оценить эффективность изменения структуры затрат.
Решение
Сведения о фактической и плановой сумме затрат по статьям в расчете на фактический объем произведенной продукции обозначим через величины 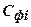 и
и 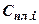 . По этим данным определяем:
. По этим данным определяем:
1. Абсолютный прирост по 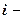 й статье затрат:
й статье затрат:
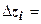
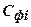 –
– 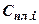 ;
; 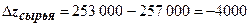 (тыс. руб.).
(тыс. руб.).
2. Процент изменения затрат по 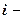 й статье:
й статье:
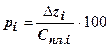 ;
; 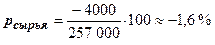 .
.
3. Процент прироста по отношению к итоговой сумме затрат (по плановой калькуляции):
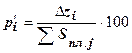 ;
; 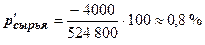 .
.
4. Удельный вес данной статьи затрат в общей сумме при плановой структуре:
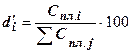 ;
; 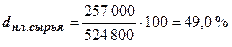 .
.
5. Фактический удельный вес в общей сумме в общих затратах:
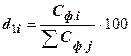 ;
; 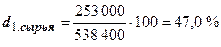 .
.
6. Изменение удельного веса данной статьи затрат:
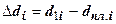 ;
; 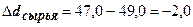 процентных пункта.
процентных пункта.
7. Возможная сумма фактических затрат по данной статье при сохранении плановой структуры:
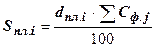 ;
; 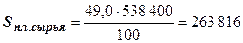 .
.
8. Прирост затрат по данной статье в связи с общим снижением или повышением затрат на производство продукции:
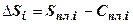 ;
; 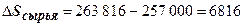 (тыс. руб.).
(тыс. руб.).
9. Прирост (уменьшение) затрат по данной статье в связи с изменением ее удельного веса в общей сумме по сравнению с затратами по данной статье при плановой структуре:
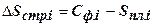 ;
; 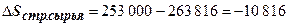 (тыс. руб.).
(тыс. руб.).
Таким образом, изменение суммы затрат по данной статье состоит из изменения за счет общего снижения или увеличения себестоимости продукции (п. 8) и изменения за счет структурных сдвигов в составе затрат (п. 9), т.е.
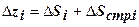 ;
; 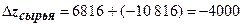 (тыс. руб.).
(тыс. руб.).
Прирост за счет структурных сдвигов можно определить и иначе, когда возможная сумма затрат (п. 7) рассчитывается исходя из распространения на сумму затрат по плановым нормативам фактической структуры себестоимости, т.е.
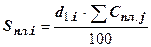 ;
; 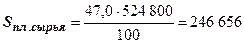 (тыс. руб.).
(тыс. руб.).
В этом случае получаем другие показатели распределения прироста.
Пример 10.
Кожевенно-обувной комбинат реализует свою продукцию через сеть клиентов с таким товарооборотом:
| Группы клиентов | Объем реализации, млн. руб. | |
| Оптовые | 1020,0 | 2000,0 |
| Мелкооптовые | 650,0 | 800,0 |
| Магазины | 600,0 | 900,0 |
| Итого: | 2270,0 | 3700,0 |
Дата добавления: 2016-07-27; просмотров: 40783;











