Д) меньше или равна нулю.
2.8. Формулы для расчета дисперсии признака:
а) 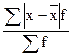 ;
;
б); 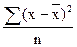 ;
;
в) 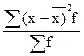 ;
;
г) 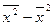 ;
;
д) 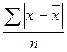 .
.
2.9. Правило мажорантности средних определяется как:
1) 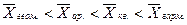
2) 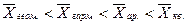
3) 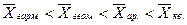
где 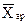 - средняя арифметическая;
- средняя арифметическая;
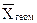 - средняя геометрическая;
- средняя геометрическая;
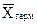 - средняя гармоническая;
- средняя гармоническая;
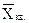 - средняя квадратическая.
- средняя квадратическая.
2.10. Медианой называется:
а) среднее значение признака в ряду распределения;
б) наиболее часто встречающееся значение признака в данном ряду;
в) значение признака, делящее совокупность на две равные части;
г) наиболее редко встречающееся значение признака в данном ряду;
д) значения признака, делящие совокупность на четыре равные части.
2.11. По ряду распределения определите моду (с точностью до 0,1):
Группы семей по размеру жилой площади, приходящейся на одного человека, м2.
15-17 17-19 19-21 21-23
Число семей с данным размером жилой площади
20 38 40 22
2.12. По ряду распределения определите медиану (с точностью до 0,1):
Группы семей по размеру жилой площади, приходящейся на одного человека, м2.
15-17 17-19 19-21 21-23
Число семей с данным размером жилой площади
20 28 30 12
2.13. Имеется ряд распределения:
Тарифный разряд рабочих: 2 3 4 5 6
Число рабочих:8 16 17 19 7
Укажите вид данного ряда распределения:
а) дискретный;
б) интервальный;
в) атрибутивный.
2.14. Имеется ряд распределения:
Тарифный разряд рабочих:
2 3 4 5 6
Число рабочих:
8 16 27 32 7
Рассчитайте средний тарифный разряд рабочих (с точностью до 0,1).
2.15. Имеется ряд распределения:
Тарифный разряд рабочих:
2 3 4 5 6
Число рабочих:
8 16 27 29 37
Рассчитайте моду.
2.16. Имеется ряд распределения:
Тарифный разряд рабочих:
2 3 4 5 6
Число рабочих:
9 26 27 29 31
Рассчитайте медиану.
2.17. Абсолютные показатели вариации:
а) размах вариации;
б) коэффициент корреляции;
в) коэффициент осциляции;
г) среднее линейное отклонение;
д) среднее квадратическое отклонение;
е) дисперсия;
ж) коэффициент вариации.
2.18. Правило сложения дисперсий выражается формулой:
1) 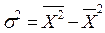 .
.
2) 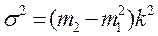
3) 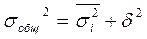
4) 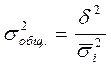
2.19. Размах вариации - это:
а) R = Хmax - 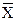 ;
;
б) R = 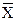 - Хmin;
- Хmin;
в) R = Хmax - Хmin;
г) R = Х - Хmin.
2.20. Формулы для расчета дисперсии:
а) 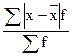 ;
;
б) 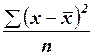 ;
;
в) 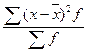 ;
;
г) 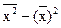 ;
;
д) 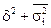 .
.
2.21. К относительным показателям вариации относятся:
а) размах вариации;
б) дисперсия;
в) коэффициент вариации;
г) среднее линейное отклонение;
д) относительное линейное отклонение.
2.22. Статистическая совокупность разбита на m групп по факторному признаку. В каждой группе исчислено среднее значение результативного признака: 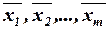 ,численность единиц в каждой группе
,численность единиц в каждой группе 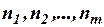 . Среднее значение в целом по совокупности можно определить по формуле:
. Среднее значение в целом по совокупности можно определить по формуле:
а) 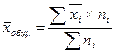
б) 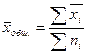
в) 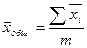
г) нельзя определить по приведенным данным
2.23. Значение моды можно определить на основе графика:
а) полигона распределения;
б) функции распределения;
в) кумуляты;
г) огивы;
д) кривой Лоренца.
2.24. Определите (с точностью до 0,1 руб.) средний уровень издержек обращения на 100 руб. товарооборота по следующим данным:
| Издержки обращения на 100 руб. товарооборота, руб. | Число предприятий | Товарооборот в среднем на одно предприятие, млн. руб. |
| 2 - 4 4 - 6 |
2.25. Определите (с точностью до 1 млн. руб.) средний размер товарооборота на одно предприятие по следующим данным:
| Издержки обращения на 100 руб. товарооборота, руб. | Число предприятий | Товарооборот в среднем на одно предприятие, млн. руб. |
| 2 - 4 4 - 6 |
2.26. Определите моду по данным о распределении работников предприятия по размеру месячной заработной платы:
| Заработная плата, руб. | Число работников |
2.27. Определите медиану по данным о распределении работников предприятия по размеру месячной заработной платы:
| Заработная плата, руб. | Число работников |
2.28. В каких пределах находится дисперсия альтернативного признака:
а) 0,5 < 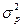 £ 1;
£ 1;
б) 0 £ 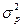 £ 0,25;
£ 0,25;
в) 0 £ 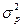 £
£ 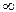 ;
;
г) 0,25 £ 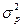 £ 1;
£ 1;
д) может принимать любое значение.
2.29. Определите моду и медиану для следующих значений признака:
3, 5, 6, 9, 9, 12, 13.
2.30. Определите моду и медиану для следующих значений признака:
3, 3,4, 4, 4, 4, 6, 6, 6.6, 6
Тема 3. Индексы
3.1. Выберите формулы для расчета индекса: а) фиксированного (постоянного) состава, б) переменного состава, в) структурных сдвигов:
а) 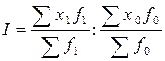 ;
;
б) 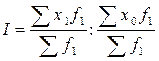 ;
;
в) 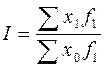 ;
;
г) 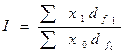 , где
, где 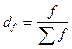 ;
;
д) 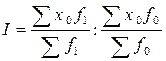 ;
;
e) 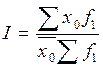 .
.
3.2. укажите название индексов:
а) 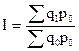 ;
;
б) 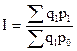 ;
;
в) 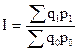 .
.
3.3. укажите название индексов:
а) 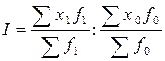 ;
;
б) 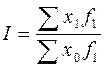 ;
;
в) 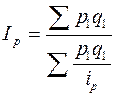 .
.
3.4. Недостающим элементом в формуле среднего арифметического индекса физического объема товарооборота является:

3.5. Записать уравнение связи между сводными индексами стоимостного объема товарооборота (Ipq), физического объема товарооборота (Iq) и цен (Ip).
3.6. Агрегатный индекс цен при исчислении по одним и тем же данным будет:
а) меньше среднего гармонического индекса цен;
б) меньше или равен среднему гармоническому индексу цен;
в) больше среднего гармонического индекса цен;
г) больше или равен среднему гармоническому индексу цен;
Дата добавления: 2016-07-27; просмотров: 3138;











