Д) равен среднему арифметическому индексу физического объема.
3.8. Агрегатные индексы цен Пааше строятся с весами:
а) текущего периода;
б) базисного периода;
в) без использования весов.
3.9. Средние индексы исчисляются как средняя величина из:
1) индивидуальных индексов;
2) цепных агрегатных индексов;
3) базисных агрегатных индексов.
3.10. Произведение промежуточных по периодам цепных индексов дает базисный индекс последнего периода, если это индексы:
а) стоимости;
б) индивидуальные;
в) цен с постоянными весами;
г) физического объема с переменными весами;
д) физического объема с постоянными весами;
е) цен с переменными весами.
3.11. Отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода, если это индексы:
а) стоимости;
б) индивидуальные;
в) цен с постоянными весами;
г) физического объема с переменными весами;
д) физического объема с постоянными весами;
е) цен с переменными весами.
3.12. При построении агрегатных индексов качественных показателей, как правило, используют веса:
а) отчетного периода;
б) базисного периода.
3.13. При построении агрегатных индексов количественных показателей, как правило, используют веса:
а) отчетного периода;
б) базисного периода.
3.14. Записать уравнение связи между сводными индексами издержек производства (Izq), физического объема продукции (Iq) и себестоимости (Iz).
3.15. Записать уравнение связи между индексом переменного состава (Iпер.сост.), индексом постоянного состава (Iпост.сост ) и индексом структурных сдвигов (Iстр.сд).
Тема 4. Ряды динамики
4.1. При исчислении среднегодового темпа роста является верной формула:
1) 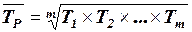 ;
;
2) 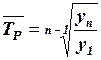 ;
;
3) 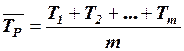 .
.
4.2. По формуле 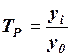 определяется:
определяется:
а) базисный темп роста;
б) цепной темп роста;
в) базисный темп прироста;
г) цепной темп прироста;
д) абсолютное значение 1% прироста.
4.3. По формуле 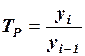 определяется;:
определяется;:
а) базисный темп роста;
б) цепной темп роста;
в) базисный темп прироста;
г) цепной темп прироста;
д) абсолютное значение 1% прироста.
4.4. Средний уровень моментного ряда динамики с равными временными промежутками между датами исчисляется по формуле:
а) средней арифметической простой;
б) средней арифметической взвешенной;
в) средней гармонической простой;
г) средней гармонической взвешенной;
д) средней хронологической простой;
е) средней хронологической взвешенной.
4.5. Средний уровень моментного ряда динамики с неравными временными промежутками между датами исчисляется по формуле:
а) средней арифметической простой;
б) средней арифметической взвешенной;
в) средней гармонической простой;
г) средней гармонической взвешенной;
д) средней хронологической простой;
е) средней хронологической взвешенной.
4.6. Средний уровень интервального ряда динамики с равными временными промежутками исчисляется по формуле:
а) средней арифметической простой;
б) средней арифметической взвешенной;
в) средней гармонической простой;
г) средней гармонической взвешенной;
д) средней хронологической простой;
е) средней хронологической взвешенной.
4.7. Средний уровень интервального ряда динамики с неравными временными промежутками исчисляется по формуле:
а) средней арифметической простой;
б) средней арифметической взвешенной;
в) средней гармонической простой;
г) средней гармонической взвешенной;
д) средней хронологической простой;
е) средней хронологической взвешенной.
4.8. Для выявления основной тенденции развития явления используются:
а) метод укрупнения интервалов;
б) метод скользящей средней;
в) аналитическое выравнивание;
г) индексный метод;
д) расчет средней гармонической.
4.9. Методом аналитического выравнивания по прямой выявлена тенденция ряда динамики: 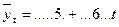
| Год | Объем выручки предприятия (y), тыс. руб. | t |
| -2 -1 +1 +2 |
Определите теоретическое значение показателя объема выручки в 1999 году.
4.10. Методом аналитического выравнивания по прямой выявлена тенденция ряда динамики: 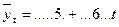
| Год | Объем выручки предприятия (y), тыс. руб. | t |
| -5 -3 -1 +1 +3 +5 |
Определите теоретическое значение показателя объема выручки в 2005 году.
4.11. По ряду динамики рассчитайте индекс сезонности для февраля (с точностью до 0,1 %):
| Месяц | Выручка, тыс. руб. | |
| Январь Февраль Март … | 27,3 25,2 27,2 … | 26,0 25,8 28,4 … |
| Итого за год | 404,0 | 416,0 |
4.12. По ряду динамики рассчитайте индекс сезонности для марта (с точностью до 0,1 %):
| Месяц | Выручка, тыс. руб. | |
| январь февраль март … | … | … |
| Итого за год | 504,0 | 516,0 |
Тема 5. Корреляционный метод
5.1. Какой коэффициент корреляции 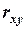 показывает наиболее тесную связь: Г
показывает наиболее тесную связь: Г
а) 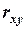 = 0,972; б)
= 0,972; б) 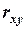 = – 0,981; в)
= – 0,981; в) 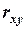 = 0,971.
= 0,971.
5.2. Какой коэффициент корреляции 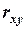 показывают обратную связь между признаками:
показывают обратную связь между признаками:
а) 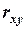 = – 0,982; б)
= – 0,982; б) 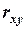 = 0,991; в)
= 0,991; в) 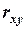 =0,871.
=0,871.
5.3. Какие коэффициенты корреляции 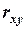 показывают прямую связь между признаками:
показывают прямую связь между признаками:
а) 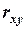 = 0,982; б)
= 0,982; б) 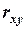 = – 0,991; в)
= – 0,991; в) 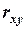 = 0,871.
= 0,871.
5.4. Межгрупповая дисперсия составляет 82% от общей дисперсии. Рассчитайте эмпирическое корреляционное отношение (с точностью до 0,01).
5.5. Простейшим приемом выявления корреляционной связи между двумя признаками является:
а) расчет коэффициента корреляции знаков;
б) расчет коэффициента эластичности;
в) построение уравнения корреляционной связи;
г) анализ корреляционного поля.
5.6. Эмпирическое корреляционное отношение представляет собой корень квадратный из отношения:
а) средней из групповых дисперсий к общей дисперсии;
б) межгрупповой дисперсии к общей дисперсии;
в) межгрупповой дисперсии к средней из групповых дисперсий;
г) средней из групповых дисперсий к межгрупповой дисперсии.
5.7. Теснота связи двух признаков при нелинейной зависимости определяется по формуле:
а) 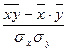 ;
;
б) 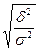 ;
;
в) 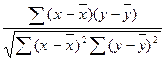 .
.
5.8. Теснота связи между двумя альтернативными признаками измеряется с помощью:
а) коэффициент корреляции знаков Фехнера;
б) коэффициент корреляции рангов Спирмена;
в) коэффициент ассоциации;
г) коэффициент контингенции;
д) коэффициент конкордации.
5.9. Парный коэффициент корреляции показывает:
а) тесноту линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель;
б) тесноту линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель;
в) тесноту нелинейной зависимости между двумя признаками;
г) тесноту связи между результативным признаком и остальными, включенными в модель.
5.10. Частный коэффициент корреляции показывает:
а) тесноту линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель;
б) тесноту линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель;
в) тесноту нелинейной зависимости;
г) тесноту связи между результативным признаком и остальными, включенными в модель.
5.11. Парный коэффициент корреляции может принимать значения:
а) от 0 до 1;
б) от –1 до 0;
в) от –1 до 1;
г) любое положительное значение;
д) любое значение меньше нуля.
5.12. Частный коэффициент корреляции может принимать значения:
а) от 0 до 1;
б) от –1 до 0;
в) от –1 до 1;
г) любое положительное значение;
д) любое значение меньше нуля.
5.13. Множественный коэффициент корреляции может принимать значения:
а) от 0 до 1;
б) от –1 до 0;
в) от –1 до 1;
г) любое положительное значение;
д) любое значение меньше нуля.
5.14. Коэффициент детерминации может принимать значения:
а) от 0 до 1;
б) от –1 до 0;
в) от –1 до 1;
г) любое положительное значение;
д) любое значение меньше нуля.
5.15. С помощью какого уравнения регрессии исследуется прямолинейная связь между факторами:
а) 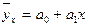 ;
;
б) 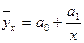 ;
;
в) 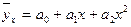 ;
;
г) 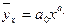 .
.
5.16. Какие формулы используются для аналитического выражения нелинейной связи между факторами:
а) 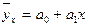 ;
;
б) 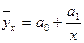 ;
;
в) 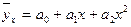 .
.
5.17. Для изучения связи между двумя признаками рассчитано линейное уравнение регрессии:
параметры: 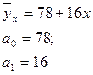
Выберите верные утверждения:
Параметр 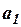 показывает, что:
показывает, что:
а) связь между признаками прямая;
б) связь между признаками обратная;
в) с увеличением значения признака “х” на единицу значение признака “у” увеличивается на …..;
г) с увеличением значения признака “х” на единицу значение признака “у” увеличивается на ….
5.18. Для изучения связи между двумя признаками рассчитано линейное уравнение регрессии:
параметры: 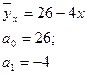
Выберите верные утверждения:
Параметр 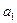 показывает, что:
показывает, что:
а) связь между признаками прямая;
б) связь между признаками обратная;
в) с увеличением значения признака “х” на единицу значение признака “у” увеличивается на …;
г) с увеличением значения признака “х” на единицу значение признака “у” уменьшается на ….
5.19. Корреляционный анализ используется для изучения:
а) развития явления во времени;
б) структуры явлений;
в) соотношений явлений;
г) взаимосвязей явлений.
5.20. В результате проведения регрессионного анализа получают функцию, описывающую:
а) взаимосвязь показателей;
б) соотношение показателей;
в) структуру показателей;
г) темпы роста показателей;
д) прирост показателей.
5.21. Если результативный и факторный признаки являются количественными, то для анализа тесноты связи между ними могут применяться:
а) корреляционное отношение;
б) линейный коэффициент корреляции;
в) коэффициент ассоциации;
г) коэффициент корреляции рангов Спирмена;
д) коэффициент корреляции знаков Фехнера.
5.22. Для анализа тесноты связи между двумя качественными альтернативными признаками могут применяться:
а) корреляционное отношение;
б) линейный коэффициент корреляции;
в) коэффициент ассоциации;
г) коэффициент корреляции рангов Спирмена;
д) коэффициент контингенции.
5.23. Параболическое уравнение регрессии применяется, если:
а) при равномерном возрастании факторной переменной результативный признак возрастает или убывает ускоренно;
б) результативный и факторный признаки возрастают или убывают примерно одинаково (в арифметической прогрессии);
в) при увеличении значений факторной переменной значения результативного признака не изменяются.
5.24. Линейное уравнение регрессии применяется, если:
а) при равномерном возрастании факторной переменной результативный признак возрастает или убывает ускоренно;
б) результативный и факторный признаки возрастают или убывают примерно одинаково (в арифметической прогрессии);
в) при увеличении значений факторной переменной значения результативного признака не изменяются.
5.25. Гиперболическое уравнение регрессии применяется, если:
а) при равномерном возрастании факторной переменной результативный признак возрастает или убывает ускоренно;
б) при увеличении значений факторной переменной значения результативного признака уменьшаются, причем это уменьшение все время замедляется;
в) при увеличении значений факторной переменной значения результативного признака увеличиваются, причем это увеличение все время возрастает;
г) результативный и факторный признаки возрастают или убывают примерно одинаково (в арифметической прогрессии).
5.26. Для определения параметров уравнения регрессии можно применить метод:
а) скользящей средней;
б) наименьших квадратов;
в) основного массива;
г) параллельных рядов.
5.27. О качестве полученного уравнения регрессии судят на основе:
а) средней ошибки аппроксимации;
б) уровня значимости;
в) доверительной вероятности;
г) частных коэффициентов корреляции.
5.28. С помощью какого графика можно определить форму зависимости между двумя признаками:
а) гистограммы;
б) кумуляты;
в) корреляционного поля;
г) огивы;
д) полигона распределения.
5.29. Установите соответствие между видом коэффициента и его формулой:
а) 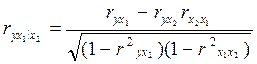 ;
;
б) 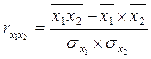 ;
;
в) 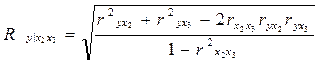 ;
;
г) 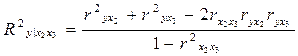 .
.
1) парный (линейный) коэффициент корреляции;
2) частный коэффициент корреляции;
3) коэффициент детерминации;
4) множественный коэффициент корреляции.
5.30. Установите соответствие между видом уравнения регрессии и названием функции, его описывающей:
а) 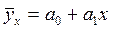 ; б)
; б) 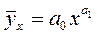 ; в)
; в) 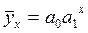 ; г)
; г) 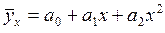 ;
; 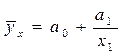 .
.
1) показательная функция; 2) линейная функция; 3) парабола; 4) степенная функция; 5) гипербола.
5.31. Установите соответствие между показателем и его назначением:
а) определяет тесноту связи между результативным признаком и несколькими факторными признаками;
б) определяет тесноту линейной зависимости между двумя признаками на фоне действия всех факторов, входящих в модель;
в) определяет тесноту линейной зависимости между двумя признаками при исключении влияния остальных.
1) парный (линейный) коэффициент корреляции;
2) частный коэффициент корреляции;
3) множественный коэффициент корреляции.
5.32. Если линейный коэффициент корреляции получился равным 0,235, то
1) связь между признаками отсутствует;
2) связь между признаками достаточная;
3) связь между признаками средняя;
4) связь между признаками либо слабая, либо нелинейная;
5) связь между признаками либо слабая, либо обратная.
5.33. Связь между процентной ставкой на межбанковский кредит (%) (у) и сроком предоставления кредита в днях (х) описана уравнением регрессии:
уx = a + bх. Это означает, что с продлением срока пользования кредитом на 1 день процентная ставка увеличится в среднем на…
5.34. Связь между балансовой прибылью предприятий (млн.руб.) (у) и числом дней просроченных платежей (х) описана уравнением регрессии:
уx = 90 – 0,2х. Это означает, что с каждым днем просроченных платежей балансовая прибыль в среднем будет уменьшаться на….
5.35. Средняя из произведений значений двух признаков x и y равна 21 ( 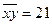 ), среднее значение факторного признака х равно 3 (
), среднее значение факторного признака х равно 3 ( 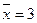 ), среднее значение результативного признака у равно 5 (
), среднее значение результативного признака у равно 5 ( 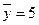 ), дисперсия факторного признака х равна 25 (σx2 = 25) , дисперсия результативного признака у равна 36 (σy2= 36). Определите линейный коэффициент корреляции (с точностью до 0,1).
), дисперсия факторного признака х равна 25 (σx2 = 25) , дисперсия результативного признака у равна 36 (σy2= 36). Определите линейный коэффициент корреляции (с точностью до 0,1).
5.36. Если теоретическое корреляционное отношение равно 1, то связь между признаками:
а) функциональная, прямая;
б) статистическая, прямая;
в) функциональная, обратная;
г) статистическая, обратная;
Д) отсутствует.
5.37. Если теоретическое корреляционное отношение равно 1, то:
а) линия регрессии проходит через все эмпирические точки;
б) линия регрессии проходит параллельно оси абсцисс;
в) линия регрессии проходит параллельно оси ординат;
Дата добавления: 2016-07-27; просмотров: 3558;











