Методика экономического анализа

В экономическом анализе широко используется на различных этапах исследования ряд специальных способов и приемов, которые условно можно подразделить на группы:

1. традиционные и нетрадиционные;

2. количественные и качественные;

3. логические;

4. экономико-математические;

5. эвристические.

Остановимся более подробно на каждой из этих групп.

К традиционным приемам и способам относятся:

1 .Использование аналитических показателей.

2. Группировка.

3. Выделение узких мест.

4. Сравнение.

5. Разработка аналитических формул.

6. Балансовый.

7. Методы цепных подстановок.

8. Интегральный метод.

9. Индексный метод.

10.Графический.

В свою очередь все традиционные приемы, кроме первого являются также логическими и количественными.

К нетрадиционным приемам и способам относятся:

1. Эвристический.

2. Маржинальный.

3. Дисконтирование.

4. Математическая статистика и теория вероятности.

5. Эконометрические.

6. Математическое программирование.

7. Иммитационное моделирование.

8. Исследование операций.

9. Классический математический анализ.

Кроме первого, всё приемы относятся к количественным, эвристический прием является также качественным. Приемы с 4-ого по 9- ый — экономико-математические.

Качественные приемы применяются в анализе тогда, когда нельзя показатели выразить количественно или когда необходимо учесть влияние некоторых качественных факторов. Все эти методы, названные также поведенческие, делятся на две группы:

· методы экспертных оценок;

· методы психологические.

В свою очередь, методы экспертных оценок подразделяются на:

– методы участия или методы интервью;

– анкетирование;

– метод номинальной группы.

К психологическим способам относятся методы «мозговой атаки».

Способ сравнения –научный метод, когда изучаемое явление сопоставляют с уже известным, изученным ранее, для определения общих черт либо различий меду ними. В экономическом анализе данный способ является одним из важнейших, так как с него начинается любой анализ.

В экономическом анализе используются разные виды относительных величин: планового задания, динамики, структуры, интенсивности, эффективности и разные типы средних величин: среднеарифметические (простые и взвешенные), среднегармонические, среднегеометрические, средне хронологические, среднеквадратические и др.

Группировка как способ анализа предполагает определенную классификацию процессов и факторов, их обусловливающих. Аналитические группировки предназначены для выявления взаимозависимости и взаимодействия между изучаемыми объектами, показателями.

Балансовый способ служит как отражение пропорций двух групп взаимосвязанных экономических показателей. Этот метод широко распространен в практике бухгалтерского учета и планирования.

Графические методы используются для быстрого нахождения значения функциональных зависимостей с помощью геометрического изображения на плоскости.

Количественные методы факторного анализа позволяют определить влияние факторов на изменение результативного показателя.

Факторный анализ, где эта зависимость носит функциональный характер, называется, как отмечалось ранее, детерминированный.

В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей:

Аддитивные:

Y= Х_i+Х₁+Х₂+Х₃+ ... +Х_n

Здесь результативный показатель представляет собой алгебраическую сумму нескольких факторов.

Мультипликативные:

Y= П Х_i = Х₁*Х₂*Х₃*…*Х_n

Данная модель применяется тогда, когда результативный показатель - произведение нескольких факторов.

Кратные:

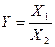
Применяются, когда результативный показатель есть частное от деления одного факторного показателя на величину другого.

Смешанные (комбинированные):

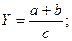
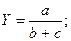
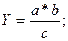
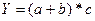и т.д.

Основными методами факторного анализа являются методы последовательного элиминирования факторов. Элиминировать - значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя кроме одного. Суть метода состоит в том, что последовательно рассчитывается влияние фактора на изменение результативного показателя при допущении, что в конкретный момент времени влияние оказывает только один фактор, а другие остаются неизменным и при условии, что факторы не связаны друг с другом.

Метод цепной подстановки используется для всех типов детерминированных моделей и является базовым факторного анализа.

Рассмотрим основные этапы его использования:

1 .Составляется модель для анализа, причем соблюдается строгая

последовательность факторов в модели:

1). Количественный фактор;

2). Структурный фактор;

3). Качественный фактор.

Y = А*В, где

А - количественный показатель;

В- качественный показатель.

2.Составление расчетов, в которых последовательно меняется уровень факторных показателей с базового на фактический. Количество таких расчетов равно количеству факторов плюс один:

Y1 =А1*В1

Y  =A2*B1

Y2 = A2*В2

3. Определение влияния факторов на изменение результативного показателя путем последовательного вычитания из каждого последующего расчета предыдущего. При этом определяется влияние того фактора, который изменяет свой уровень в этих двух расчетах:

∆У (А)= У’ -УI

∆У (В)= У2-У’

4.Балансовая увязка результатов вычислений состоит в том, что общее изменение результативного показателя должно быть равно сумме его изменений под влиянием всех факторов в модели:

∆У =∆У(А)+∆У(В)

Метод абсолютных разниц - это сокращенный вариант метода цепных подстановок и используется только в мультипликативных и смешанных моделях типа: Y=( а-Ь )*с и Y=а*(b-c)и рассчитывается умножением абсолютного прироста исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.

Например, в модели Y=а*b*с ∆а=Аф –Апл.; ∆b=Вф-Впл.; ∆с=Сф-Спл.

Yа=∆а*Впл.Спл.

Yb=Аф*∆b*Спл.

Yс=Аф*Вф*∆с

Способ относительных разниц, (его еще называют индексным методом или методом разниц в %), как и предыдущий применяется в мультипликативных моделях, а также в комбинированных типа (У= а-b)*c.Он значительно проще цепных подстановок и в некоторых случаях делает его очень эффективным (например, когда исходные данные уже содержат определенные ранее относительные отклонения факторных показателей). Сущность данного мётода рассмотрим на предыдущей модели. Сначала необходимо рассчитать относительные отклонения факторных показателей:

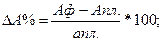
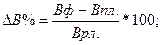
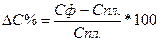
Тогда отклонение результативного показателя за счет каждого фактора определяется следующим образом:

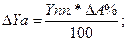
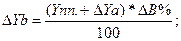
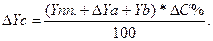
Способ пропорционального деления используется в аддитивных и смешанных моделях типа Y, = а/ b + с + d +... + n. Рассмотрим на модели типа Y, =а + b=с. Расчет будет выглядеть следующим образом:

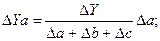
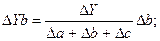
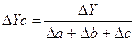
Используя модели детерминированного анализа, рассмотренные ранее, на основе элиминирования исходят из того, что факторы изменяются независимо друг от друга. В действительности же факторы изменяются совместно и взаимодействуя друг с другом оказывают влияние на результативный показатель. дополнительный прирост при этом присоединяется при элиминировании к одному из факторов, как правило к последнему. Поэтому величина влияния факторов на результативный показатель зависит от места, на которое поставлен тот или иной фактор в детерминированной модели.

Интегральный метод, который применяется в мультипликативных и смешанных моделях (сочетание кратной и аддитивной моделей), позволяет избежать этого недостатка. Дополнительный прирост результативного показателя, образованный от взаимодействия факторов раскладывается между ними пропорционально их воздействию на результативный показатель. Представим в общем виде интегральный метод. Формулы, используемые при анализе модели ГХУ выглядят следующим образом:

∆Fx = ∆X*Yo + ½*∆X*∆Y

∆Fy = ∆Y*Xo + ½*∆X*∆Y

На практике не все экономические явления можно изучать, используя четкую функциональную зависимость. Стохастические зависимости отличаются приблизительностью, неопределенностью. В данном случае для определения тесноты связи между показателями, не находящимися в функциональной зависимости, широко используется метод корреляционного и регрессионного анализа. Отличают парную и множественную корреляцию. Парная - это связь между двумя показателями. Множественная, когда с результативным показателем взаимодействует несколько факторов. Теснота связи между изучаемыми явлениями измеряется корреляционным отношением. Необходимыми условиями для применения корреляционного анализа являются наличие достаточно большого количества наблюдений о величине факторных и результативных показателей и исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации.

Способы оптимизации показателей и экономико-математических методов включают в себя:

1.Методы линейного программирования для решения экстремальных задач, часто встречающихся в экономике. Решение таких задач сводится к нахождению крайних значений (max и min). Оно основано на решении системы линейных уравнений, когда зависимость между изучаемыми явлениями строго функциональна. Одним из примеров является транспортная задача, решение которой сводится к выбору из всех допустимо возможных (альтернативных) вариантов лучшего, оптимального. Задачи решаются двумя способами: симплекс-методом и распределительным методом;

2.Теория игр - теория математических моделей исследует оптимальные стратегии в ситуации игрового характера. К ним относятся ситуации, связанные с выбором наивыгоднейших производственных решений, хозяйственных взаимоотношений между предприятиями различных форм собственности, между хозяйственными субъектами и коммерческими балками. Ситуацию можно представить как игру двух, трех и более игроков, каждый из которых преследует цель максимизации своей выгоды за счет, своего выигрыша за счет другого игрока. Количество стратегий у каждого игрока может быть конечным и бесконечным, отсюда и игры подразделяются на конечные и бесконечные. На промышленных предприятиях теория игр может использоваться для выбора оптимальных решений при создании рациональных запасов сырья, материалов, п/ф,, в вопросах качества продукции и др.;

3.Теормя массового обслуживания - вероятностные модели реальных систем обслуживания населения, при котором время обслуживания будет минимальным, а качество высоким, не будет излишних затрат.

Кроме экономико-математических моделей, применяемых на макроуровне, существует – экономико-математическое моделирование микроуровневых финансовых ситуаций:

1. Модели операций дисконтирования - обусловлено неравноценностью одинаковых по абсолютной величине сумм денежных средств сегодня и в будущем. Дисконтирование позволяет учитывать в операциях фактор времени. Различают математическое дисконтирование, коммерческий или банковский учет.

2. Модели финансовых потоков отражают целый ряд последовательных платежей: по заключенным договорам, по погашению банковского кредита и т.п., распределенных во времени.

3. Модели инфляции, с помощью которых устанавливается количественное соотношение по определенно влияния инфляции на показатели финансовой операции.

4. Модели операций с облигациями. В процессе моделирования операций с облигациями применяются различные показатели: курс, цена, доходность облигаций; определяется общий доход по операции покупки погашения облигации.

5. Модели операций с акциями. Как и в предыдущих моделях при анализе операций с акциями необходимо проводить расчеты по нескольким показателям: доходность, курсовая стоимость, рыночная цена акций, доходность от финансовых операций с акциями.

6. Модели сравнения эффективности операций. Для выбора выгодной схемы финансовой или коммерческой операции необходимо проводить их сравнение. При расчете эффективности финансовых операций используют сравнительную доходность, которая на основе допущения в равенстве финансовых результатов различных вариантов инвестиций приводит к понятно эквивалентных ставок простых или сложных процентов. Это позволяет получить инструмент корректного сравнения финансовых операций.

К наиболее эффективным методам хозяйственной деятельности с целью выявления резервов экономии затрат материальных, трудовых и денежных ресурсов на производство продукции относится функционально-стоимостной анализ (ФСА).

ФСА возник в конце 40-х годов ХХ века. Почти одновременно американский инженер Л.д. Майлз (фирма «Gеnеral Е1еktrik») и российский Ю.М. Соболев (Пермский телевизионный завод) предложили качественно новые подходы к поиску резервов снижения себестоимости изделия. Узел усиления микротелефона, предложенный Соболевым, позволил сократить количество деталей на 70%, затраты материалов - на 42%, трудоемкость -на 69%, а общую себестоимость - в 1,7 раза. На Западе, в отличие нашей страны, этот метод быстро завоевал всеобщее признание И сегодня на крупнейших фирмах, каждый доллар, затраченный на проведение ФСА, дает экономию от 7 до 20 долларов в зависимости от отрасли и объекта исследования. У нас этот метод наибольшее совершенство достиг лишь в электротехнической промышленности.

В чем же заключается сущность данного метода? Если рассматривать последовательность поиска резервов сокращения затрат, то она очевидна для аналитика: сравнение фактических сумм затрат по определенным статьям и элементам с нормативными. Положительные отклонения и считаются резервами.

ФСА основывается на утверждении что каждый продукт, объект и т. д. существует и вырабатывается для того, чтобы удовлетворять определенные потребности, т.е. выполнять определенные функции. Но используя тот или иной предмет, можно увидеть, что он выполняет не одну, а всегда несколько функций, которые можно разделить на:

– основные, выполняющие главную функцию;

– выполняющие дополнительную роль;

– ненужные функции.

Отсюда, если функции не нужны, то и затраты на их создание также лишние. Поэтому ФСА всё затраты подразделяют на функционально необходимые для выполнения объектом его функционального назначения и на излишние затраты в результате несовершенства конструкторских решений. Кроме того, необходимо отметить, что каждая функция может быть выполнена разными способами путем разного технологического и технического решения, и соответственно, требует разных объемов затрат. Выбирал тот или иной способ осуществления определенной функции, можно заранее определить минимальную сумму затрат на ее создание.

Таким образом, ФСА - это метод поиска более дешевых способов выполнения главных функций путем организационных, технических, технологических и др. изменений производства при одновременном исключении лишних функций.