Система уравнений Максвелла

Первое уравнение Максвелла в интегральной формеявляется обобщением закона электромагнитной индукции Фарадея в форме

.

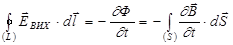Согласно Максвеллу этот закон справедлив не только для проводящего контура, но и для любого замкнутого контура, мысленно выбранного в переменном магнитном поле. Иными словами, с переменным магнитным полем независимо от того, находятся в нём проводники или нет, неразрывно связано вихревое электрическое поле.

Переменное электрическое поле, так же как и электрический ток, является источником магнитного поля. Количественной мерой магнитного действия переменного электрического поля служит ток смещения. Плотностью тока смещенияназывается вектор:

.

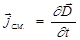Второе уравнение Максвелла в интегральнойформе: циркуляция вектора напряжённости магнитного поля по произвольному контуру L равна алгебраической сумме макротоков и тока смещения сквозь поверхность, натянутую на этот контур (рис. 2.21) и находится по формуле

,

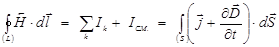где 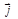- плотность тока проводимости; I_СМ.- ток смещения.

Третье уравнение Максвелла в интегральной форме

,

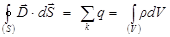где r - объемная плотность свободных электрических зарядов.

Четвёртое уравнение Максвелла в интегральной форме

.

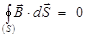Систему уравнений Максвелла необходимо дополнить так называемыми материальными уравнениями, характеризующими электрические и магнитные свойства среды.

В случае изотропных несегнетоэлектрических и неферромагнитных сред и макротоков, подчиняющихся закону Ома, эти уравнения имеют вид

, , ,

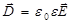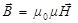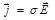где e₀, m₀ - электрическая и магнитная постоянные; e, m - относительные диэлектрическая и магнитная проницаемости среды; s - удельная электрическая проводимость среды.