Примеры решения задач. Определить индукцию магнитного поля

1. Квадратная рамка со стороной а=2 см, содержащая 100 витков, подвешена на упругой нити с постоянной кручения С=10 мкН×м/град. Плоскость рамки совпадает с направлением линий индукции внешнего магнитного поля. Определить индукцию магнитного поля, если при пропускании по рамке тока I=1А она повернулась на угол j=60^о.

Решение. Рамка будет находиться в равновесии, когда результирующий момент сил, действующий на рамку, равен нулю, т.е. 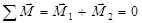, где М₁- момент сил, действующих на рамку с током со стороны магнитного поля; М₂ - момент упругих сил.

М₁ = р_m B sin a,

где р _m = NIS = NIa² - магнитный момент рамки; В - индукция магнитного поля; a - угол между вектором 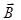и нормалью к плоскости рамки. Как видно из рисунка, угол a=90°–j =30°.

М₂=Сj.

Из условия равновесия

Ia²NB sin a - Сj = 0,

откуда

B = Сj/(Ia²NB sin a).

Подставим числовые значения:

В = 10 ^-3×60 / 1×4×100×0,5 = 30 мТл.

2. Прямой бесконечный проводник имеет круговую петлю радиусом R=80 см. Определить силу тока в проводнике, если известно, что в точке А магнитная индукция B = 12,5 мкТл.

Решение. По принципу суперпозиции индукция магнитного поля в точке А равна векторной сумме индукций магнитных полей, созданных бесконечно длинным проводником с током I (В₁) и круговым током в его центре (В₂):

.

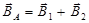Векторы В₁ и В₂ на рисунке в точке А будут направлены в одну сторону перпендикулярно плоскости рисунка от нас, тогда можно записать

,

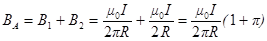откуда

.

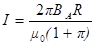Подставим числовые значения:

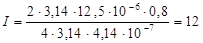А.

3. Квадратная рамка расположена в одной плоскости с длинным прямым проводником с током I₀ =5 А. Сторона рамки 8 см. Проходящая через середины противоположных сторон ось рамки параллельна проводу и отстоит от него на расстоянии, которое в n = 1,5 раза больше стороны рамки. Найти поток вектора 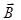через поверхность рамки.

Решение

Прямой проводник с током создает вокруг себя неоднородное магнитное поле с индукцией

,

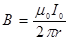которая уменьшается с увеличением расстояния от проводника. Направление вектора индукции будет совпадать с направлением нормали к рамке. Так как магнитное поле неоднородное, поверхность, ограниченную рамкой, разобьём на элементарные площадки dS = a×dr, в пределах которых магнитную индукцию можно считать постоянной величиной (см. рисунок). Тогда поток магнитной индукции (магнитный поток) через элементарную площадку

dФ _m = B·dS·cos 0° = B×а×dr = m ₀I₀ ·a·dr/(2pr).

Полный поток вектора 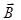через поверхность рамки

.

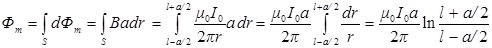Подставим числовые значения:

Ф_m = 4p×10^–7×5×0,08×(ln 2)/2p = 5,545×10^–8 Вб.

4. Между полюсами электромагнита требуется создать магнитное поле с индукцией В=1,4 Тл. Длина железного сердечника l₁=40 см, длина межполюсного пространства l₂=1 см, диаметр сердечника D=5 см. Какую ЭДС нужно взять для питания обмотки электромагнита, чтобы получить требуемое магнитное поле, используя медную проволоку площадью поперечного сечения S=1 мм ²? Какая будет при этом наименьшая толщина b намотки, если считать, что предельно допустимая плотность тока j=3 МА/м ²?

Решение

Так как силовые линии магнитного поля замкнуты, то магнитный поток и индукция магнитного поля в сердечнике и в воздушном зазоре одинаковы: В₁=В₂. Для решения задачи воспользуемся теоремой о циркуляции вектора 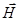(т.к. циркуляция 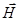определяется только макротоками и не зависит от наличия или отсутствия магнетика). Выберем замкнутый контур вдоль силовой линии и вычислим циркуляцию вектора напряжённости:

,

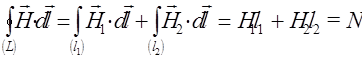где Н₁ и Н₂ - напряжённости магнитного поля в сердечнике и вне его; l₁ и l₂ – длина железного сердечника и межполюсного пространства.

Так как H₂ = B₂/m₀ = B₁/m₀, то

H₁l₁ + B₁l₂/m₀ = NI. (1)

Поскольку величина В₁ известна по условию задачи, то величину Н₁ найдём из графика зависимости В = В(H) (прил. 1):

при В = 1,3 Тл, Н = 800 А/м.

Из уравнения (1) определим число ампер-витков электромагнита:

(NI) = 800×0,4 + 1,3×0,01/(4×3,14×10^–7) = 1,07×10⁴ А-вит.

Величину ЭДС e вычислим по закону Ома:

e=IR_пров = Irl _пров/S = IrpDN / S = IrpDN / S.

Подставим числовые значения:

e = 1,7×10^–8×3,14×0,05×1,07×10⁴/10^–6 = 29 В.

Для определения толщины обмотки нужно знать общее число витков N и число витков N₁ в одном слое обмотки.

N₁ = l₁/d,

где l₁ – длина сердечника; d – диаметр провода обмотки: d = 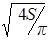, тогда

N₁ = l₁/ 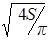= 0.4 / 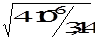= 354 витка .

Зная число ампер–витков и предельно допустимое значение силы тока (I=jS), определим общее число витков N

N = (NI)/(jS) = 1,07×10 ⁴ / (3×10⁶×10^–6) = 3567 витков.

Число слоёв

k = N/N₁ = 3567/354 » 10.

Тогда толщина обмотки

b = d×k = k× 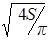= 10× 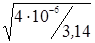= 11,3×10 ^-3 м » 11 мм.

5. Квадратная рамка с током I=1 А расположена в одной плоскости с длинным прямым проводником с током I₀=5 А. Сторона рамки 10 см. Ось рамки, проходящая через середины противоположных сторон, параллельна проводу и отстоит от него на расстоянии, которое в n = 1,5 раза больше стороны рамки. Найти:

1) силу, действующую на рамку;

2) работу, которую нужно совершить для поворота рамки вокруг её оси на 180°, если токи поддерживают неизменными.

Решение

1. Прямой длинный проводник с током I₀ создаёт вокруг себя неоднородное магнитное поле с индукцией B₀=m₀I_o/2pr, которая уменьшается с увеличением расстояния от проводника. В таком магнитном поле на каждую сторону квадратной рамки с током будет действовать сила Ампера, направление которой можно определить по правилу левой руки, а величину - по формуле F_A=IB₀lsin a.

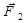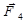Как видно из рисунка (при указанных направлениях силы тока в проводниках), l=a, a=90° (sin a =1), силы и противоположны по направлению и равны по величине

.

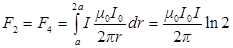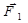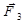Следовательно, результирующая этих двух сил равна нулю. Силы и противоположны по направлению, но не равны по величине:

F₁ = Im₀I₀a /2pa = m₀I₀I /2p.

F₃ = Im₀Ia /2p2a = m₀I₀I /4p.

Так как сила F₁ в два раза больше силы F₃, то результирующая этих сил будет совпадать по направлению с силой F₁, а по величине

F = F₁ – F₃ = m₀I₀I /2p – m₀I₀I /4p = m₀I₀I /4p.

Подставим числовые значения

F = 4p×10^–7×1×5/4p = 5×10^–7 Н = 0,5 мкН.

2. Работу, необходимую для поворота рамки с током I на 180°, можно определить по формуле

А = IDФ_m = I(Ф_2m – Ф_1m),

где Ф_1m и Ф_2m - магнитные потоки через поверхность рамки в начальном и конечном состояниях. Так как магнитное поле проводника с током I₀ неоднородное, сначала определим магнитный поток через элементарную площадку dS=adr, в пределах которой индукцию магнитного поля можно считать постоянной величиной:

dФ_m = B₀dS cos a,

а полный магнитный поток сквозь рамку в начальном и конечном состояниях

.

.

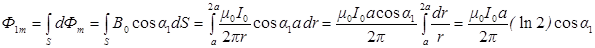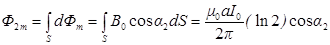Так как a₁ = 0°, a₂ = 180°, (cosa₁ = 1, cosa₂ = –1), то

DФ_m = Ф_2m – Ф_1m = – m₀aI₀ (ln 2)/2p – m₀aI₀ (ln 2)/2p = –m₀aI₀ (ln 2)/p.

Работа

А = IDФ_m = –m₀aI₀I (ln 2)/p.

Подставим числовые значения:

А = –4p×0,1×1×5×0,69×10^–7/p » –1,4×10^–7 Дж = –0,14 мкДж .

6. Тонкий металлический стержень длиной l = 1,2 м вращается в однородном магнитном поле вокруг перпендикулярной к стержню оси, отстоящей от одного из его концов на расстоянии а=0,25 м, делая n=120 об/мин. Вектор магнитной индукции поля параллелен оси вращения и имеет величину В=10^–3 Тл. Найти разность потенциалов U, возникающую между концами стержня.

Решение

Разность потенциалов между концами стержня будет равна по величине ЭДС индукции, возникающей в стержне за счёт вращения

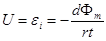. (1)

Для однородного магнитного поля и плоской поверхности dФ_m=BdScosa, или, подставив в (1), получаем (знак минус опустим, так как необходимо найти только величину ЭДС)

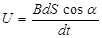. (2)

По условию задачи cosa =1, поэтому из выражения (2) следует

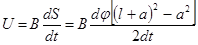, (3)

dj = wdt = (2pn)dt. (4)

Подставляя (4) в (3), получим:

.

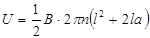U = 10^–3×2p×2 (1,2² + 2×1,2×0,25)/2 = 0,0128 В = 12,8 мВ.

7. Прямой проводник длиной l=10 см помещён в однородное магнитное поле с индукцией В=1 Тл. Концы проводника замкнуты гибким проводом, находящимся вне поля. Сопротивление внешней цепи R=0,4 Ом. Какая мощность потребуется для того, чтобы двигать проводник перпендикулярно линиям индукции с постоянной скоростью u=20 м/с?

Решение

Проведём анализ условия задачи. При движении проводник будет пересекать линии индукции. За счёт этого в проводнике возникнет ЭДС индукции

e = – dФ/dt, (1)

где в данном случае

dФ = BdS = Bludt . (2)

Подставляя (2) в (1), получаем:

e = – Blu.

Сила индукционного тока в цепи согласно закону Ома

I = e / R = – (Blv)/R.

Тепловая мощность, выделяемая на внешнем сопротивлении

P = I²R = B²l²u²/R.

Эта мощность будет равна мощности, которую необходимо подводить к системе за счёт внешней силы, действующей на проводник, для того, чтобы скорость движения проводника была постоянной. Таким образом:

P = B²l²u²/R = 1×0,01×400/0,4 = 10 Вт.

8. Две катушки равномерно намотаны на цилиндрический сердечник, длина которого много больше диаметра. Индуктивность первой катушки 0,2 Гн, второй- 0,8 Гн. Сопротивление второй катушки 600 Ом. Какой ток потечёт по второй катушке, если ток в 0,3 А, текущий в первой катушке, выключить в течение времени 0,001 с.

Решение

Данная задача относится к разделу взаимной индукции. Сила тока во вторичной обмотке

I₂ = e₂/R₂. (1)

Величина e₂ зависит от взаимной индуктивности L₁₂ и быстроты изменения силы тока I₁

e ₂ = –L₁₂dI₁/dt = –L₁₂DI₁/Dt = –L₁₂(I₁ – I₀₁)/Dt. (2)

Взаимная индуктивность двух соленоидов, имеющих общий сердечник, рассчитывается по формуле

L₁₂ = mm₀n₁n₂lS. (3)

Собственные индуктивности

L₁ = mm₀n₁²lS, (4)

L₂ = mm₀n₂²lS, (5)

поэтому, учитывая выражения (3), (4), (5), получаем

L₁₂ = 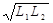. (6)

Подставляя выражение (6) в выражение (2), а полученный результат - в выражение (1), получаем:

I₂ = (L₁₂I ₀₁)/R₂ = (I₀₁ 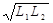)/R₂Dt.

I₂ = 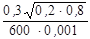= 0,2 А.

9. На тороид квадратного поперечного сечения намотано 1000 витков провода. Внутренний радиус тороида равен 0,1 см, внешний - 0,2 см. Магнитная проницаемость тороида равна100. По обмотке тороида протекает электрический ток силой 1 À. Определить энергию магнитного поля внутри тороида.

Решение

Решим задачу двумя способами.

1. Энергия магнитного поля – это энергия, запасённая в индуктивности:

,

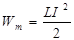где L - индуктивность, I - сила тока, протекающего в индуктивности.

Потокосцепление, согласно определению индуктивности, рассчитывается как

Y = LI, Y = NФ_m,

где Ф_m - магнитный поток через поперечное сечение S тороида.

,

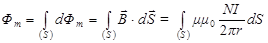где r - расстояние от центра тороида до площадки dS, на которой определяется величина индукции магнитного поля. Так как тороид квадратного сечения, то высота площадки h = (r ₂ - r ₁), а ширина - dr. Поэтому

.

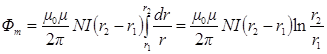Тогда индуктивность тороида

L = 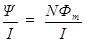= 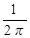mm₀N ² (r₂ - r₁)ln .

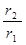Подставляя выражение для индуктивности в выражение для энергии, получаем

.

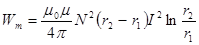W_m = 100×4p×10^–7×10⁶×10^–3×1×ln2 /(4p) = 6,9 мДж.

2. Энергия магнитного поля W_m связана с плотностью энергии w_m соотношением:

W_m = ,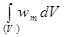

где w _m = mm₀Н ²/2.

Внутри тороида

Н = NI/l = NI/2pr.

Выберем в качестве элемента объема dV объем цилиндрического слоя радиусом r, высотой h=(r₂ - r₁) и толщиной dr (в пределах этого слоя величина Н постоянна). Запишем выражение для dV=(r₂ – r₁)2pr·dr и подставим в выражение для энергии W_m. Получаем

W _m = 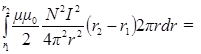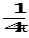mm ₀N ² I ²(r ₂ - r ₁)ln .

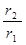Подставим числовые значения и получим:

W = 6,9 МДж.

Как видим, оба решения дают одно и то же значение.

Примечание: если в условии задачи величина m не задана, а указано, что тороид представляет собой железный, стальной или чугунный сердечник, то величина m находится по графику зависимости В = В(Н) (прил. 1) как

m = В/m ₀Н.

В качестве величины Н принять значение Н в центральной точке поперечного сечения тороида.