Энергия магнитного поля в неферромагнитной изотропной среде

При создании в замкнутом проводящем контуре электрического тока I необходимо совершить работу А по преодолению ЭДС самоиндукции, препятствующей нарастанию тока в контуре

.

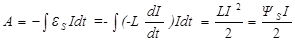В отсутствие гистерезиса окружающей среды работа А определяет магнитную энергию тока в контуре

.

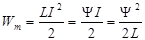Магнитная энергия тока представляет собой не что иное, как энергию его магнитного поля. Например, энергия W_m длинного соленоида, магнитное поле которого можно считать однородным и локализованным внутри соленоида, рассчитывается как

,

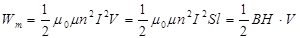где n - количество витков на единицу длины соленоида; S - площадь поперечного сечения соленоида; l - длина соленоида; m - относительная магнитная проницаемость среды внутри соленоида; I - сила тока в соленоиде.

Объёмной плотностью энергии w _m магнитного поляназывается энергия этого поля, заключенная в единице объема пространства:

.

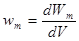В изотропной, однородной и неферромагнитной среде

.

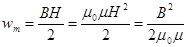Энергия W_m, локализованная в объёме V, определяется следующим образом

.

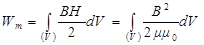Энергия магнитного поля, создаваемого произвольной системой из n контуров с токами

,

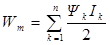где I_k - сила тока в k-м контуре, Y_k - потокосцепление этого контура. Потокосцепление

Y_k = Y_ks + Y_{k вз},

где Y_ks - потокосцепление самоиндукции k-го контура, Y_{k вз} - потокосцепление взаимной индукции k-го контура со всеми остальными контурами системы. Энергия магнитного поля системы токов

.

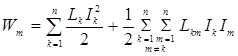Первый член представляет собой сумму собственных энергий всех токов. Второй член называется взаимной энергией токов (L_km - взаимная индуктивность k-го и m-го контуров с токами I_k и I_m).