Рассмотрим поглощение ультразвуковых волн. 3 глава

Сложные по своей структуре жидкости, в том числе и кровь, имеют кривую течения, которая отличается от ньютоновской.

Все неньютоновские жидкости состоят из сложных и крупных молекул, например растворы-полимеры. Их вязкость значительно больше, чем у простых жидкостей. Увеличение вязкости происходит потому, что при течении этих жидкостей работа внешней силы затрачивается не только на преодоление истинной ньютоновской вязкости, но и на разрушение структуры.

Кровь по своим свойствам близка к концентрированным суспензиям деформируемых частиц. Неньютоновское поведение крови отчетливо обнаруживается при течении в трубах малого диаметра или при небольших скоростях сдвига ( ). Кровь - это всеобъемлющая органическая система, отражающая малейшие изменения, едва заметные сдвиги, происходящие в организме при отклонении от нормы, то есть кровь - чувствительный индикатор состояния организма.

С точки зрения реологических представлений, кровь относится к вязкопластичным жидкостям.

Для характеристики реологического поведения вязкопластичных жидкостей вводится понятие кажущейся, или эффективной, вязкости. Кажущаяся вязкость по своему физическому смыслу является положительной величиной. Она не зависит от кинематических и динамических характеристик движения.

Для вязкопластичных жидкостей, к которым относится кровь, течение начинается лишь после превышения некоторого порога, который называется «порогом текучести» (l₀). Величина l₀ характеризует пластические свойства среды, а наклон кривой течения к оси у - ее подвижность.

В этом случае уравнение, характеризующее кривую течения для неньютоновских жидкостей, примет вид:

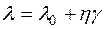. (10.6)

По поводу определения предела текучести l₀ имеется немало различных мнений. Различают статические и динамические предельные напряжения сдвига. Первые характеризуют прочность внутренней структуры жидкости и число, равное тому напряжению сдвига, при котором жидкость начинает течение из положения равновесия. Таким образом, реологическому параметру l₀ придается смысл физико-химической структурной характеристики.

10.2. Гемодинамика крови. Уравнение Пуазейля и Бернулли

Наблюдается два вида течения - ламинарное и турбулентное. Если при своем течении жидкость разделяется на слои, которые скользят друг относительно друга, не перемешиваясь, такое течение называется ламинарным. Ламинарные течения – стационарные.

При увеличении скорости или поперечных размеров потока характер течения изменяется. Возникает перемешивание жидкости. Такое течение называется турбулентным. При данном течении скорость частиц в каждом данном месте все время беспорядочно изменяется. Течение становится нестационарным. Английский ученый О. Рейнольдс установил, что характер течения зависит от безразмерной величины

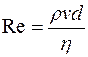, (10.7)

где r - плотность жидкости, кг/м³;

v- средняя, по сечению трубки, скорость потока, м/с;

h - динамический коэффициент вязкости, Па·с;

d - диаметр трубки, м.

При малых значениях числа Рейнольдса наблюдается ламинарное течение. Начиная с некоторого определенного значения числа Рейнольдса, называемого критическим, течение приобретает турбулентный характер.

Отношение m=h/r называется кинематической вязкостью.

Таким образом, число Рейнольдса можно записать как:

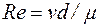. (10.9)

Характер течения различных жидкостей в трубках разных сечений будет одинаков, если каждому течению соответствует одно и то же значение Re. Таким образом, число Рейнольдса может служить критерием, характеристикой течения жидкостей в трубках разной конфигурации. Течение крови в артериях является ламинарным. Незначительная турбулентность возникает вблизи клапанов сердца. При патологии, когда изменяется вязкость, число Рейнольдса может превысить критическое значение. Течение станет турбулентным. Турбулентное течение связано с дополнительной затратой энергии, что приводит к добавочной работе сердца.

При турбулентном течении возникают шумовые явления, которые могут быть использованы с диагностической целью. Так, например, шум прослушивается на плечевой артерии при измерении давления крови методом Короткова. Течение крови подчиняется уравнению Пуазейля.

10.2.1. Уравнение Пуазейля

Течение вязкой жидкости по трубам круглого сечении для биологии и медицины имеет особое значение, так как кровеносная система состоит в основном из цилиндрических сосудов разного диаметра.

При движении жидкости в круглой трубе скорость равна нулю у стенок трубы и максимальна - на оси трубы.

Полагая течение ламинарным, найдем закон изменения скорости с расстоянием r от оси трубки: 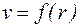. Выделим выбрасываемый цилиндрический объем жидкости радиуса r и длины l (рис. 10.3). При стационарном течении в трубе постоянного сечения скорость всех частиц становится неизменной. Таким образом, сумма внешних сил, приложенных к любому объему жидкости, равна нулю.

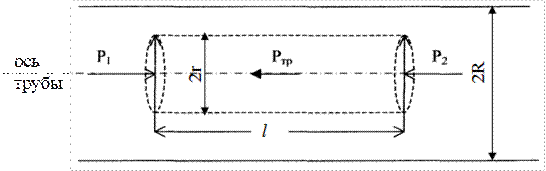
Рис. 10.3. Срез цилиндрического сосуда

На основании рассматриваемого цилиндрического объема действующие силы давления можно рсчитать по формуле

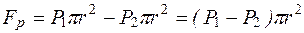. (10.9)

2. На боковую поверхность цилиндра со стороны окружающего слоя жидкости действует сила внутреннего трения, которая согласно уравнению Ньютона:

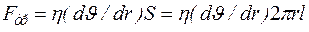, (10.10)

где 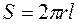- площадь боковой поверхности цилиндра.

Так как жидкость движется равномерно, то силы, действующие на выделенный цилиндр, уравновешены: .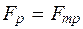

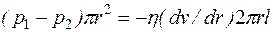. (10.11)

Знак минус в правой части уравнения обусловлен тем, что 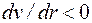(скорость уменьшается с увеличением r).

Из последнего уравнения имеем:

; (10.12)

интегрируя, получим

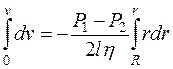. (10.13)

Нижние пределы соответствуют слою, «прилипшему» к внутренней поверхности трубки ( 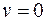при r=0), а верхние пределы — переменные. Решая уравнение, получим параболическую зависимость :

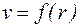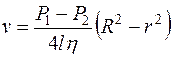. (10.14)

Наибольшую скорость имеет слой, текущий вдоль оси трубы (r=0).

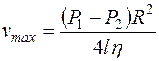. (10.15)

За единицу времени слой переносит объем жидкости, равный , тогда

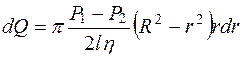. (10.16)

Интегрирование по всему объем даст

. (10.17)

Согласно формуле Пуазейля, поток жидкости пропорционален перепаду давления на единицу длины трубы, радиусу в четвертой степени и обратно пропорционален вязкости жидкости. Формула Пуазейля применима только для ламинарного течения жидкости. Проведем аналогии между формулой Пуазейля и законом Ома. Тогда величина является гидравлическим сопротивлением. Оно тем больше, чем выше вязкость жидкости и длина трубки и чем меньше площадь поперечного сечения. Более общее выражение уравнения Пуазейля, справедливое для труб переменного сечения, имеет вид:

. (10.18)

Данное уравнение показывает, что давление вдоль трубки переменного сечения убывает пропорционально: 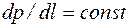. Так как Q постоянно, то градиент давления больше в трубах меньшего радиуса.

Если найти значение радиуса и подставить его в уравнение Пуазейля (10.18), то получим зависимость расхода от давления в упругих трубках

. (10.19)

Из уравнения (1.11) нйдем

; (10.20)

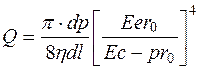. (10.21)

Измерения давления в разных участках кровеносной системы, с учетом формулы (10.21), показали, что:

1) наибольшее падение давления происходит в малых кровеносных сосудах, то есть в артериолах и капиллярах, так как в них наибольшее сопротивление;

2) сопротивление течению при расчете скорости кровотока подобно электрическому сопротивлению;

3) исходя из выражения формулы Пуазейля 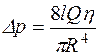, можно предположить, что 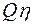характеризует величину кровотока.

10.2.2. Уравнение Бернулли

Два столетия назад член Петербургской академии наук Даниил Бернулли впервые предложил основную теорему гидродинамики, которая устанавливает связь между давлением и сопротивлением в некоторой точке струи в идеальной жидкости. С данного периода начинает развиваться наука гидродинамика, которая изучает вопросы перемещения жидкостей и взаимодействие их при этом с окружающими твердыми телами. Леонард Эйлер, современник Бернулли, вывел "общие принципы движения жидкости" и применил методы теории сплошных сред для изучения движения крови в сердечно-сосудистой системе, тем самым положив начало развитию науки гемодинамики, то есть области биомеханики, в которой рассматривается движение крови по сосудистой системе. То есть физической основой гемодинамики является гидродинамика.

После работ академика Л. Эйлера вопросы кровообращения неизменно привлекали внимание представителей точных наук.

Если в движущейся жидкости касательная к каждой точке совпадает по направлению с вектором скорости, то линии можно обозначить как линии тока, плотность которых пропорциональна скорости в данном месте текущей жидкости. Таким образом, по картине линий тока можно судить не только о направлении, но и о величине вектора скорости в разных точках пространства.

Если вектор скорости в каждой точке пространства остается постоянным, то течение называют стационарным. Линии тока при стационарном течении совпадают с траекториями частиц.

Часть жидкости, ограниченную линиями тока, называют трубкой тока. Возьмем трубку тока, у которой в каждом ее сечении скорость - величина постоянная (рис. 10.4).

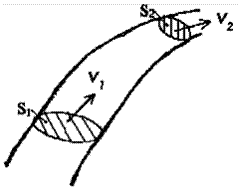
Рис. 10.4. Движение идеальной жидкости по наклонной трубе

Раз жидкость несжимаема, то количество жидкости между сечениями S₁ и S₂ будет неизменным. Отсюда следует, что объемы жидкостей, протекающих за единицу времени через сечения S₁ и S₂, будут одинаковыми, то есть

S₁v₁=S₂v₂. (10.22)

Tаким oбразом, величина Sv есть величина постоянная (Sv=const). Это есть теорема о неразрывности струи. Жидкость, в которой внутреннее трение (вязкость) полностью отсутствует, называется идеальной. Выделим в стационарно текущей жидкости трубку тока малого сечения (рис. 10.5).

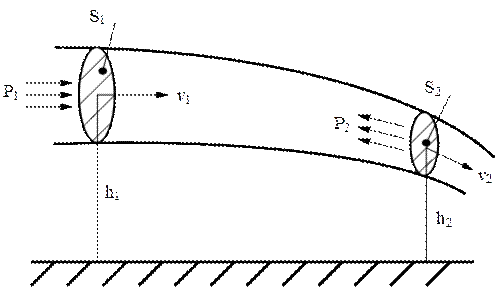
Рис. 10.5. Движение идеальной жидкости с разным сечением и давлением

Энергия каждой движущейся частицы жидкости складывается из ее кинетической энергии и потенциальной.

По закону сохранения энергии для рассматриваемого тока жидкости можно записать Е₁-Е₂=А, то есть приращение полной энергии сечения равно работе, совершаемой силами давления, которую можно выразить следующим образом:

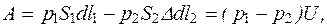(10.23)

где 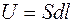- объем протекающей жидкости через данное сечение.

Таким образом,

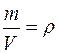, . (10.24)

Учитывая, что 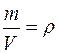, разделим (10.24) на объемы и сгруппируем члены по индексам, в итоге получим:

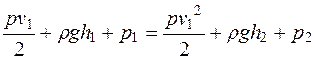, (10.25)

где v - скорость течения жидкости.

Сечения S₁ и S₂ были взяты произвольно, поэтому можно утверждать, что в любом сечении трубки тока

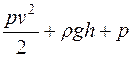=const. (10.26)

Таким образом, в стационарно текущей идеальной жидкости вдоль любой линии тока сумма динамического, статического и гидростатического давлений есть величина постоянная. Для горизонтальной трубки уравнение имеет вид:

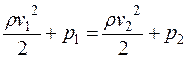, (10.27)

то есть давление меньше в тех точках, где скорость больше.

Это положено в основу устройства ингаляторов, широко используемых в физиотерапевтической практике.

Динамическое давление измеряется изогнутой трубкой, которая называется трубкой Пито. Статическое давление определяют горизонтальной трубкой. Разность давлений данных трубок делят пополам:

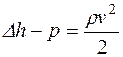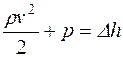; . (10.28)

Система соединенных трубок дает возможность рассчитать скорость потока жидкости по формуле

, (10.29)

при 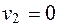, так как трубка горизонтальна.

Часто используется дифференциальный манометр, который дает значение p₁ и p₂ или проградуирован в единицах скорости. Такие манометры используются в хирургических целях при измерении давления в аорте.

Рассмотрим движение жидкости и крови по трубам с эластичными стенками. Стенки сосудов (артерий, вен и т.д.) эластичны. При сокращении сердечной мышцы (систола) кровь выбрасывается в аорту и отходящие от нее артерии. Крупные артерии, вследствие эластичности, за время систолы принимают большие количества крови, в сравнении с тем, сколько ее оттекает к периферии.

Систолическое давление в норме у человека примерно равно 120 мм рт.ст. Во время расслабления сердца (диастолы) растянутые артерии впадают, и потенциальная энергия, сообщенная им сердцем, переходит в кинетическую энергию тока крови. При этом поддерживается диастолическое давление 80 мм рт.ст. Длительность систолы вдвое меньше диастолы. Сердце 2/3 времени отдыхает. Скорость распространения пульсовой волны 6-8 м/с. В норме течение крови во всей сосудистой системе, как уже отмечалось, имеет ламинарный характер. Количество крови, протекающее через поперечное сечение сосуда в единицу времени, называется объемной скоростью кровотока. Она зависит от разностей давлений и общего сопротивления току крови, то есть

, (10.30)

где X - гидравлическое сопротивление, Па·с/м.

Сосуды располагаются в равных направлениях, но чаще всего они параллельны. Следовательно,

X=1/X₁+1/X₂+ ... +1/Х_n. (10.31)

Более 70% падения давления приходится на артерии и артериолы. В сети венозных сосудов, площадь сечения которых в два раза больше площади сечения артерий, скорость течения крови невысока и давление незначительно.

Изменение распределения крови в организме при перегрузках может оказать существенное влияние на функционирование органов. Поэтому очень важно, чтобы в этих условиях тело человека располагалось соответствующим ситуации образом относительно направления сил.

10.3. Физические закономерности движения крови в сосудистой системе. Пульсовая волна

Сосудистая система состоит из артерий, артериол, капилляров, венул и вен, которые соединены как последовательно, так и параллельно друг с другом. Артериолы, капилляры и венулы представляют собой систему параллельно соединенных сосудов.

Начальным звеном сосудистой системы является аорта в большом круге кровообращения и легочная артерия - в малом. Конечным звеном являются крупные вены. Движение крови по сосудам, энергию движущейся крови и изменение давления на протяжении сосудистого русла описывают уравнениями Бернулли и Пуазейля. В единицу времени протекает одинаковый объем крови: Sv=const.

Движение крови ламинарно. Выходя из аорты, кровь движется по разветвляющимся элементам и попадает в капилляры, общее сечение которых в 600-800 раз больше сечения аорты. Исходя из формулы (10.22), скорость течения крови в капиллярах во столько же раз меньше скорости крови в аорте ( м/с; в капиллярах мм/с).

Замедление тока крови в капиллярах имеет важное физиологическое значение, так как при большой скорости кровь не успевала бы обмениваться кислородом и растворенными в ней веществами с клетками и тканями.

Стенки кровеносных сосудов неодинаковы по своему строению. Крупные артерии состоят из мышечных волокон, эластина и коллагена. Эластин имеет деформацию 200%, коллаген - ≈ 10%. С уменьшением диаметра сосуда артериолы (d ≤ 100 мкм) почти полностью состоят из мышечной ткани, растяжимость которой значительно меньше. По венам кровь течет с малой скоростью v ≈ 10 мм/с и при низком давлении (15-20 мм рт.ст.). Внутри вен имеются пластины, препятствующие обратному течению крови. Течение крови по эластичным сосудам обладает определенной спецификой. Кровь, попадая в такой сосуд, его растягивает, и объем крови в этом участке увеличивается. Затем, когда давление со стороны насоса падает, стенка сосуда сокращается, и потенциальная энергия стенки переходит в кинетическую энергию жидкости. В результате этого избыток жидкости из начального участка переходит в следующий ее участок.

Растяжение и постепенное сжатие сосуда обеспечивает равномерное протекание крови. Деформация стенки распространяется вдоль сосуда и образует так называемую пульсовую волну. Скорость пульсовой волны приблизительно определяется по формуле

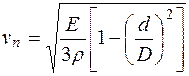, (10.32)

где Е - модуль упругости стенки сосуда, Па;

D и d - внешний и внутренний диаметры сосуда, мкм;

ρ - плотность жидкости, кг/м³.

Рассмотрим пульсовое давление в крупных артериях.

Пусть из левого желудочка кровь поступила в артерию. Стенки сосуда расширяются, его исходный радиус получит приращение (r+ε). Толчок крови и связанное с ним давление (р) распространяются вдоль сосуда: ε = Δr. Предположим, что вторая производная от приращения (изменения) радиуса артерии 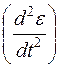пропорциональна градиенту давления с обратным знаком:

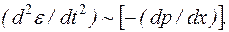(10.33)

Перейдем к равенству

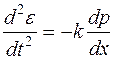, (10.34)

где k=1/r.

таким образом,

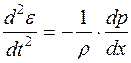. (10.35)

Данное уравнение называется фундаментальным уравнением движения Кинга.

Из уравнения (1.11), путем выражения движения крови через производную радиуса, получим:

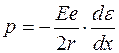, (10.36)

где e - толщина стенки, м;

r - внутренний радиус сосуда, м.

Найдем производную 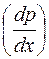из данного уравнения и подставим в уравнение (10.35). получим

. (10.37)

Данное уравнение называется уравнением Юнга-Кортевека.

Путем введения эмпирического множителя, который связывает скорость распространения пульсовых колебаний с другими факторами, получим, идентичную с формулой (10.32) формулу

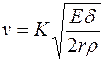, (10.38)

где δ - толщина стенки сосуда, м;

Таким образом, из приведенного уравнения можно сделать вывод, что скорость распространения пульсовой волны пропорциональна корню квадратному от жесткости сосуда (модуля упругости артерии). Измерение скорости кровотока может быть использовано для измерения эластичности стенок артериальной системы. Полученные данные могут играть большую роль в диагностике сердечно-сосудистых заболеваний.

Для диагностики сердечно-сосудистых заболеваний большую роль также играет вязкость крови, характеризующая реологическое поведение кровотока.

10.4. Клинические методы определения вязкости крови

В клинике относительный коэффициент вязкости определяется с помощью медицинского вискозиметра (рис. 10.6).

1. Капиллярный метод основан на формуле Пуазейля .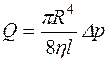

Он заключается в измерении времени протекания через капилляр жидкости известной массы под действием силы тяжести при определенном перепаде давлений.

Капиллярные вискозиметры (см. рис. 10.6, а) измеряют вязкость от 10^-5 Па·с до 10⁴ Па·с.

2. Ротационные вискозиметры. В этих вискозиметрах жидкость находится в зазоре между двумя соосными телами, например цилиндрами. Один из цилиндров вращается, а другой неподвижен. Вязкость измеряется по угловой скорости ротора, который создает определенный момент силы на неподвижном цилиндре, или по моменту силы, действующему на неподвижный цилиндр, при заданной угловой скорости вращения ротора.

Рис. 10.6. Капиллярный вискозиметр (а) и вискозиметр Гесса (б): М₁ и М₂ - метки, обозначающие границы резервуаров; 1, 2 – капилляры; 3 - приемные сосуды

В ротационных вискозиметрах можно измерить градиент скорости, задавая разные угловые скорости вращения ротора. Это позволяет измерять вязкость при разных градиентах и установить зависимость , которая характерна для ньютоновских жидкостей. С помощью ротационных вискозиметров определяют вязкость жидкостей в интервале 1…10⁵ Па·с.

3. B клинике для определения вязкости крови используют вискозиметр Гесса (см. рис. 10.6, б). Посредством резиновой груши трубки 3 заполняют капилляр 1 до нулевой отметки, а капилляр 2 - исследуемой жидкостью. Секундомером засекают время истечения жидкости.

Для расчета используют формулу Пуазейля .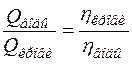

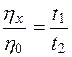. (10.39)

отношение вязкости крови к вязкости воды называется относительной вязкостью крови. У здорового человека η_п=0,4…0,5 Па·с, при патологии η_п=0,17…2,29 Па·с.

Коэффициент вязкости крови, кроме как от температуры, зависит от скорости ее движения по сосудам. В крупных сосудах η меньше, чем в капиллярах.

Суммарный объем форменных элементов крови в процентах по отношению ко всему объему крови называется гематокритом. Величина гематокрита ф=30-40ε₀, таким образом кровь — суспензия. Этим она отличается от ньютоновских жидкостей. Вязкость цельной крови в относительных единицах ; вязкость плазмы - h_пл = (1,7-2,2).

Отношение между h_кр и h_пл определяется величиной гематокрита и может быть описано рядом эмпирических формул, например:

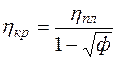. (10.40)

На основании вышесказанного можно сделать следующие выводы.

Течение крови по сосудам является ламинарным. Гидродинамика крови как сложной коллоидной суспензии, характеризуется уравнениями Пуазейля и Бернулли.

Переход ламинарного течения крови в турбулентное возникает чаще всего при патологических состояниях сосудов – варикозного расширения вен, пороков сердца и т.д.

Большую роль в жизнедеятельности организма играет реологическое поведение кровотока.

Методы измерения вязкости крови, их усовершенствование, в настоящее время приобретают большое диагностическое значение.

Решение практических задач вычислительного характера, которые предлагаются после вопросов для самопроверки, несомненно играют определенную роль для закрепления учебного материала рассмотренной главы, знание которого необходимо для будущего специалиста, связанного с биологией и медициной.

Вопросы для самопроверки

1. В чем сущность физической модели жидких тел по теории Френкеля?

2. Напишите уравнение Бернулли и дайте его формулировку.

3. Как измерить статическое и динамическое давление?

4. Как выразить зависимость критической скорости от значения кинетической вязкости и через число Рейнольдса?

5. Сделайте вывод уравнения Пуазейля.

6. Что изучает наука реология?

7. В чем сущность закона Ньютона для текущей жидкости?

8. Какие жидкости называются ньютоновскими и неньютоновскими?

9. Постройте графики кривых течения ньютоновских и неньютоновских жидкостей.

10. Какая вязкость называется кажущейся?

11. Что выражает уравнение Юнга-Кортевека?

12. В чем сущность вискозиметрии?

Задачи для закрепления изучаемого материала

1. Определить максимальное количество крови, которое может пройти через аорту за 1 с, чтобы течение сохранялось ламинарным. Диаметр аорты 2·10^-2 м, вязкость крови 5 Па·с.

2. Наблюдая под микроскопом движение эритроцитов в капилляре, можно измерить скорость течения крови 0,5 мм/с. Средняя скорость тока крови в аорте составляет около 40 см/с. На основании этих данных определить, во сколько раз сумма поперечных сечений всех функционирующих капилляров больше сечения аорты.

3. Из горизонтально расположенного медицинского шприца, диаметром 1,5 см, выдавливается физиологический раствор силой 10 Н. Найти скорость вытекания жидкости из иглы шприца. Плотность физиологического раствора равна 1603 г/см³. Сечение поршня значительно больше сечения иглы. Почему скорость вытекания раствора не зависит от сечения иглы?

4. Найти скорость и время полного оседания сферических частиц радиусом 2 мкм в двух случаях:

а) при действии силы тяжести;

б) при центрифугировании с n=500^-1, радиус центрифуги равен 10 см. действием силы тяжести пренебречь.

5. Диаметр поршня шприца равен 15 мм, внутренний диаметр иглы - 0,5 мм. Какое давление врач должен прикладывать к поршню, чтобы время инъекции составляло 10 с? Длина хода поршня 7 см. Плотность вводимого лекарственного раствора принять равной плотности воды, то есть ρ=10^-3 кг/м³.

6. Рассчитать скорость пульсовой волны в артериях, для которых отношение d/Д=0,9. Модуль Юнга для стенки артерии равен E=10⁶ H/м².

7. Определить максимальное количество крови, которое может пройти через аорту в 1 с, чтобы течение сохранилось ламинарным. Диаметр аорты 2·10^-2 м. Вязкость крови η=6 Па·с.

8. В цилиндрическом сосуде высотой 10 см, с внутренним диаметром 5 см, вращается сыворотка крови. Градиент скорости ее вблизи поверхности сосуда равен 2 с^-1. Определить вязкость сыворотки крови, если момент силы, действующей со стороны жидкости на стакан, равен 7,9·10^-7 Н·м.

9. Определить скорость эритроцитов, двжущихся с потоком крови в сонной артерии, если доплеровская частота при отражении ультразвука от эритроцитов оказалась 1,7 кГц. Частота ультразвука, падающего под углом 60º к оси артерии, равна 3 МГц, а скорость его в крови равна 1,5 км/с.

10. Какая разность давлений поддерживается на участке артерии внутренним диаметром 3 мм и длиной 10 см, если объемный поток крови через артерию составляет 2·10^-5 м³/с? Коэффициент вязкости крови 5 мПа·с.