Теорема про циркуляцію вектора індукції магнітного поля

Розрахунки магнітного поля струмів часто спрощуються при врахуванні симетрії в конфігурації струмів, що створюють поле. В цьому випадку розрахунки можна виконувати за допомогою теореми про циркуляцію вектора магнітної індукції, яка в теорії магнітного поля струмів грає ту ж роль, що і теорема Гауса в електростатиці.

Пояснимо поняття циркуляції вектора B. Нехай в просторі, де створено магнітне поле, вибраний деякий умовний замкнутий контур і вказаний позитивний напрям обходу контуру. На кожній окремій малій ділянці Δlцього контуру можна визначити дотичну складову B_l вектора B в цьому місці, тобто визначити проекцію вектора B на напрям дотичної до цієї ділянки контуру (рис. 3.38).

Циркуляцією вектора B називають суму добутків B_l·Δl, узяту по усьому контуру L, або інтеграл:

. (3.54)

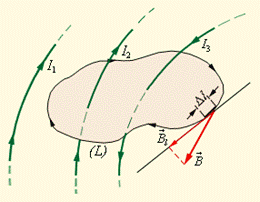
Рисунок 3.38.

Замкнутий контур (L) із заданим напрямом обходу. Зображені струми I₁, I₂ і I₃, що створюють магнітне поле.

Деякі струми, що створюють магнітне поле, можуть пронизувати вибраний контур L в той час, як інші струми можуть знаходитися в стороні від контуру.

Теорема про циркуляцію стверджує, що циркуляція вектора B магнітного поля постійних струмів у вакуумі по будь-якому контуру L завжди дорівнює добутку магнітної сталої μ₀ на суму усіх струмів, що пронизують контур:

. (3.55)

В якості прикладу на рисунку 4.37 зображено декілька провідників із струмами, що створюють магнітне поле. Струми I₂ і I₃ пронизують контур L в протилежних напрямах, тому знаки у струмів повинні бути різні - позитивними вважаються струми, які пов'язані з вибраним напрямом обходу контуру правилом правого гвинта. Отже, I₃ > 0, а I₂ < 0. Струм I₁ не пронизує контур L.

Теорема про циркуляцію в цьому прикладі виражається співвідношенням:

.

Простим прикладом застосування теореми про циркуляцію є визначення магнітної індукції поля прямолінійного провідника із струмом. Враховуючи симетрію в цьому завданні, контур L доцільно вибрати у вигляді кола деякого радіусу R, що лежить в перпендикулярній провідникові площині. Центр кола знаходиться в деякій точці провідника. В силу симетрії вектор B спрямований по дотичній (B_l·= B), а його модуль однаковий в усіх точках кола. Застосування теореми про циркуляцію призводить до співвідношення:

,

звідки слідує формула для модуля магнітної індукції поля прямолінійного провідника із струмом

.

Ця формула співпадає з виразом (3.52), отриманим із закону Біо-Савара-Лапласа.

Цей приклад показує, що теорема про циркуляцію вектора магнітної індукції може бути використана для розрахунку магнітних полів, створюваних симетричним розподілом струмів, коли з міркувань симетрії можна "вгадати" загальну структуру поля.

Є немало практично важливих прикладів розрахунку магнітних полів за допомогою теореми про циркуляцію. Одним з таких прикладів є завдання обчислення поля тороїдальної котушки (рис. 3.39).

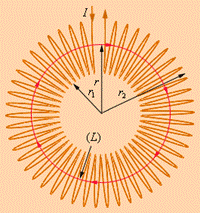
Рисунок 3.39.

Передбачається, що котушка щільна, тобто провід виток до витка намотаний на немагнітний тороїдальний сердечник. У такій котушці лінії магнітної індукції замикаються усередині котушки і є концентричними колами. Вони спрямовані так, що дивлячись уздовж них, ми побачили б струм у витках, циркулюючим за годинниковою стрілкою. Одна з ліній індукції деякого радіусу r₁ ≤ r < r₂ зображена на рисунку 3.39. Застосуємо теорему про циркуляцію до контуру L у вигляді кола, співпадаючого із зображеною на рисунку 3.39 з лінією індукції магнітного поля. З міркувань симетрії ясно, що модуль вектору В однаковий уздовж усієї цієї лінії. По теоремі про циркуляцію можна записати:

B·2πr = μ₀IN, B ·2πr = μ0IN,

де N - повне число витків, а I – сила струму, що протікає по витках котушки. Отже,

. (3.56)

Таким чином, модуль вектора магнітної індукції в тороїдальній котушці залежить від радіусу r. Якщо сердечник котушки тонкий, тобто r₂ - r₁ << r, то магнітне поле усередині котушки практично однорідне. Величина n = N/2πr є числом витків на одиницю довжини котушки. В цьому випадку

B = μ₀In .(3.57)

У цей вираз не входить радіус тора, тому воно справедливе і в граничному випадку
r → ∞. Але в межі кожну частину тороїдальної котушки можна розглядати як довгу прямолінійну котушку. Такі котушки називають соленоїдами.

На рисунку 3.40 зображено магнітне поле котушки кінцевої довжини. Слід звернути увагу на те, що в центральній частині котушки магнітне поле практично однорідне і значно сильніше, ніж поза котушкою. На це вказує густина ліній магнітної індукції. У граничному випадку нескінченно довгого соленоїда однорідне магнітне поле цілком зосереджене усередині соленоїда.

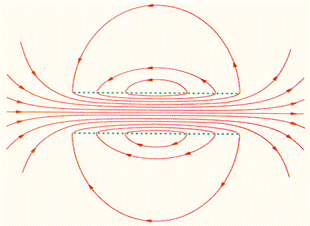
Рисунок 3.40.

У разі нескінченно довгого соленоїда вираз для модуля магнітної індукції можна отримати безпосередньо за допомогою теореми про циркуляцію, застосувавши її до прямокутного контуру, показаного на рисунку 3.41.

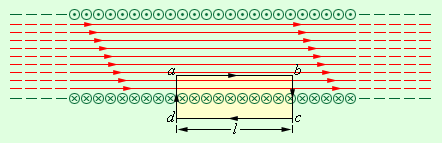
Рисунок 3.41.

Вектор магнітної індукції має відмінну від нуля проекцію на напрям обходу контуру abcd тільки на стороні ab. Отже, циркуляція вектора В по контуру рівна Bl, де l - довжина сторони ab. Число витків соленоїда, що пронизують контур abcd, дорівнює n · l, де n - число витків на одиницю довжини соленоїда, а повний струм, що пронизує контур, рівний Inl. Згідно з теоремою про циркуляцію,

Bl = μ₀Inl,звідки B = μ₀In.

Сила Лоренца

Сила Ампера, діюча на відрізок провідника довжиною Δl із струмом I, що знаходиться в магнітному полі B

F = IBΔl sin α,

може бути виражена через сили, діючі на окремі носії заряду.

F_Л = qvB sin α. (3.58)

Цю силу називають силою Лоренца. Кут α в цьому виразі дорівнює куту між швидкістю і вектором магнітної індукції. Напрям сили Лоренца, діючої на позитивно заряджену частинку, так само, як і напрям сили Ампера, може бути знайдений за правилом лівої руки. Взаємне розташування векторів v, B і F для позитивно зарядженої частинки показаний на рисунку 3.42.

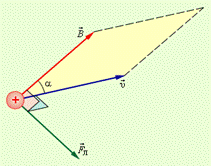
Рисунок 3.42.

Взаємне розташування векторів v, B і F. Модуль сили Лоренца чисельно дорівнює площі паралелограма, побудованого на векторах v і B помноженої на заряд q.