Спецификация модели

Все предыдущие рассуждения и выводы, касающиеся классической множественной регрессии, основывались на предположении, что мы имеем дело с правильной спецификацией модели. Под спецификацией модели в данном случае (т.е. для модели линейной множественной регрессии при выполнении предпосылок МНК) будем понимать выбор объясняющих переменных. В этой связи важное значение приобретает рассмотрение двух вопросов, имеющих смысл именно во множественной регрессии, когда исследователь имеет дело с несколькими факторами: возможная мультиколлинеарность факторов и частная корреляция. Последняя особенно тесно связана с процедурами пошагового отбора переменных.

Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность. Например, в модели урожайности качество почвы задается в виде баллов; в модели стоимости объектов недвижимости учитывается место нахождения недвижимости: районы могут быть проранжированы.

2. Факторы не должны быть коррелированы между собой и тем более находиться в точной функциональной связи.

Включение в модель факторов с высокой взаимной корреляцией, когда, например, 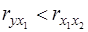, для зависимости 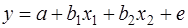может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми. Так, в приведенной зависимости с двумя факторами предполагается, что факторы х₁ и х₂ независимы друг от друга, т.е. 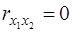. Тогда можно говорить, что параметр b₁ измеряет силу влияния фактора х₁ на результат у при неизменном значении фактора х₂. Если же 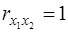, то с изменением фактора х₁ фактор х₂ не может оставаться неизменным. Отсюда b₁ и b₂ нельзя интерпретировать как показатель раздельного влияния х₁ и х₂ на у.

Как было сказано ранее, добавление нового фактора в регрессии приводит к возрастанию коэффициента детерминации и уменьшению остаточной дисперсии. Однако эти изменения могут быть незначительны, и не каждый фактор целесообразно вводить в модель.

Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико – экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы, исходя из сущности проблемы; на второй – анализируется матрица показателей корреляции и устанавливается, какие из факторов наиболее тесно связаны с результатом, а какие – между собой.