Обобщенный метод наименьших квадратов

При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется обычный метод наименьших квадратов заменить на обобщенный метод наименьших квадратов.

Этот метод применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют наименышие выборочные дисперсии. Особенности применения данного метода для корректировки данных при автокорреляции остатков будет рассмотрена в п. 4. Рассмотрим специфику применения метода обобщенных наименьших квадратов для корректировки гетероскедастичности.

При установлении гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Вид преобразования зависит от того, известны или нет дисперсии отклонений .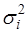

В случае, если дисперсии отклонений известны для каждого наблюдения, применяется методвзвешенных наименьших квадратов(ВНК). Гетероскедастичность устраняется, если разделить каждое наблюдаемое значение на соответствующее ему значение дисперсии.

Рассмотрим для простоты ВНК на примере парной регрессии:

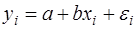(57)

Разделим обе части (57) на известное :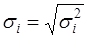

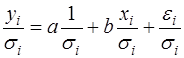(58)

Сделаем замены переменных:

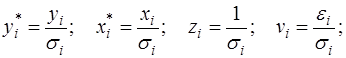(59)

получим уравнение регрессии без свободного члена, но с двумя факторами и с преобразованным отклонением:

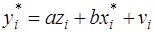(60)

Можно показать, что для v_i выполняется условие гомоскедастичности. Поэтому для модели (60) выполняются все предпосылки МНК, и оценки, полученные по МНК, будут наилучшими линейными несмещенными оценками.

Таким образом, наблюдения с наименьшими дисперсиями получают наибольшие «веса», а наблюдения с наибольшими дисперсиями – наименьшие «веса». Поэтому наблюдения с меньшими дисперсиями отклонений будут более значимыми при оценке параметров регрессии, чем наблюдения с большими дисперсиями. При этом повышается вероятность получения более точных оценок.

Полученные по МНК оценки параметров модели (60) можно использовать в первоначальной модели (57).

Для применения ВНК необходимо знать фактические значения дисперсий отклонений 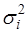. На практике такие значения известны крайне редко. Поэтому, чтобы применить ВНК, необходимо сделать реалистические предположения о значениях 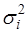. Чаще всего предполагается, что дисперсии отклонений пропорциональны или значениям x_i, или значениям .

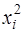Если предположить, что дисперсии пропорциональны значениям фактора x, т.е.

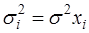(61)

тогда уравнение (57) преобразуется делением его левой и правой частей на :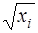

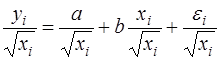
или

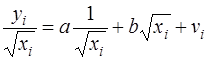(62)

Здесь для случайных отклонений 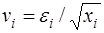выполняется условие гомоскедастичности. Следовательно, для регрессии (62) применим обычный МНК. Следует отметить, что регрессия (62) не имеет свободного члена, но зависит от двух факторов. Оценив для (62) по МНК коэффициенты а и b, возвращаемся к исходному уравнению регрессии.

Если в уравнении регрессии присутствует несколько объясняющих переменных, вместо конкретной переменной x_j используется исходное уравнение множественной регрессии

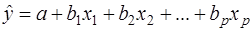
т.е. фактически линейная комбинация факторов. В этом случае получают следующую регрессию:

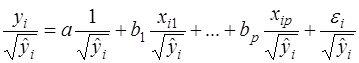(63)

Если предположить, что дисперсии 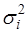пропорциональны 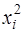, то соответствующим преобразованием будет деление уравнения регрессии (57) на x_i:

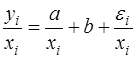
или, если переобозначить остатки как :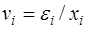

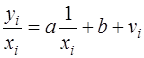(64)

Здесь для отклонений v_i также выполняется условие гомоскедастичности. Применяя обычный МНК к регрессии (64) в преобразованных переменных

,

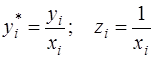получим оценки параметров, после чего возвращаемся к исходному уравнению (57). Отметим, что в регрессии (64) по сравнению с исходным уравнением параметры поменялись ролями: свободный член а стал коэффициентом, а коэффициент b – свободным членом.