ОСНОВНЫЕ ТЕОРЕМЫ КОМБИНАТОРИКИ.
2.1. Перестановки.
Число перестановок Р из n различных элементов (от французского слова permutation, что и означает перестановка) равно произведению всех натуральных чисел от 1 до n: Первый элемент в перестановке из n элементов можно выбрать n способами, второй (после выбора первого) можно выбрать (n-1) способами, третий – (n-2) способами и т. д. Перемножая способы выбора 1-го элемента со способами выбора 2-го, со способами выбора 3-го элемента и т. д, (принцип произведения) получим 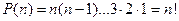 способов. Таким образом,
способов. Таким образом, 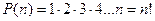 При этом полагают 0! =1! = 1.
При этом полагают 0! =1! = 1.
Пример. Назовём словом любую конечную последовательность букв русского алфавита без повторений. Сколько различных слов можно получить, переставляя буквы слова КНИГА? (Ясно, что все буквы различны. Буква К может занимать любое из 5 мест, но тогда буква Н может занимать любое из 4 мест и т.д. Таким образом, всего можно получить 5!=120 слов.)
Пример. В русском алфавите 33 различные буквы. Сколько слов, содержащих по 5 букв, можно составить, если не допускать слов, в которых две одинаковые буквы идут подряд? (Будем выбирать буквы одну за другой - сначала первую, потом вторую, третью, четвертую, пятую. Первую букву можно выбрать 33 способами - все 33 буквы русского алфавита. Вторую букву можно выбрать лишь 32 способами - ведь она должна отличаться от первой, третью букву можно выбрать тоже 32 способами - она должна отличаться от второй; четвертую и пятую буквы тоже можно выбрать 32 способами. А всего получается 33. 32 • 32 • 32 • 32 = 34 603 008 различных слов, удовлетворяющих поставленному условию.)
2.2.Перестановки с повторениями.
Пусть имеется множество, состоящее из n элементов, причем среди них n1 элементов 1-го типа; n2 элементов 2-го типа и т.д., nk элементов k-гo типа, причем nl+n2+...+nk =n. Число перестановок с повторениями из n элементов обозначают 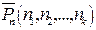 и вычисляют по формуле
и вычисляют по формуле 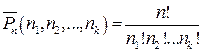 .
.
Её можно получить так: если бы все n элементов были различными, число перестановок из них равнялось бы n! Чтобы исключить из них перестановки, полученные перестановками одинаковых элементов, разделим на произведение 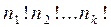
Пример. Сколько различных слов можно получить, переставляя буквы слова МАТЕМАТИКА? (Ясно, что если бы все буквы были бы различны, то таких слов было бы 10!. Но буква А повторяется 3 раза, а буквы М и Т по 2 раза. Таким образом, всего можно получить 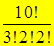 слов.)
слов.)
2.3. Упорядоченные множества. Размещения без повторений.
Будем понимать под кортежем любую последовательность конечного числа элементов. Образование кортежей можно наглядно представить себе следующим образом. Поместим элементы множества Х в мешок и будем извлекать их из него один за другим, записывать извлеченный элемент и класть обратно в мешок. После того как мы сделаем n извлечений, получим один из кортежей длины n, состоящих из элементов множества Х, или размещение с повторениями. Предположим теперь, что мы не возвращаем извлеченные элементы обратно в мешок. Тогда в полученном кортеже не будет повторяющихся элементов. Он будет состоять из n различных элементов, расположенных в определённом порядке. Такие кортежи называют упорядоченными. Одно и то же множество можно упорядочить разными способами (например, множество школьников в классе можно упорядочить по возрасту, по алфавиту, росту, по весу, и так далее).
Число способов, которыми можно упорядочить такие кортеж и называют размещениями без повторений. Формализуем задачу: пусть имеется множество, содержащее n различных элементов. Каждое его упорядоченное подмножество, содержащее m элементов, называют размещением из n элементов по к без повторений. Число размещений из n элементов по k обозначают 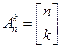 (от французского слова arrangement, что и означает размещение) и вычисляют по формуле
(от французского слова arrangement, что и означает размещение) и вычисляют по формуле 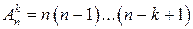 или
или 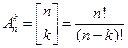 . Выражение
. Выражение 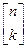 читается, как квадратная энка. В самом деле: первый элемент в размещении из n элементов по k можно выбрать n способами, второй (после выбора первого) можно выбрать (n-1) способами, третий – (n-2) способами и т. д., - k й – (n- k +1) способами. Варьируя способы выбора 1-го элемента со способами выбора 2-го, со способами выбора 3-го элемента и т. д. и, наконец, со способами выбора – k-того элемента, получим n(n - l) ... (n- k+ 1) способов. Таким образом, размещение из n элементов по n без повторений и есть перестановка.
читается, как квадратная энка. В самом деле: первый элемент в размещении из n элементов по k можно выбрать n способами, второй (после выбора первого) можно выбрать (n-1) способами, третий – (n-2) способами и т. д., - k й – (n- k +1) способами. Варьируя способы выбора 1-го элемента со способами выбора 2-го, со способами выбора 3-го элемента и т. д. и, наконец, со способами выбора – k-того элемента, получим n(n - l) ... (n- k+ 1) способов. Таким образом, размещение из n элементов по n без повторений и есть перестановка.
2.4. Размещения с повторениями.
Размещениями из n элементов по k называют упорядоченные k-элементные множества, составленные из различных элементов, причём элементы в множествах могут повторяться. Число размещений с повторениями из n по k обозначается 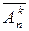 и вычисляется по формуле
и вычисляется по формуле 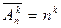 . В самом деле: 1-й элемент можно выбрать n способами, 2-й элемент – также n способами и т. д., k-й элемент можно выбрать также n способами. Тогда, в соответствии с принципом произведения, сразу получаем этот результат.
. В самом деле: 1-й элемент можно выбрать n способами, 2-й элемент – также n способами и т. д., k-й элемент можно выбрать также n способами. Тогда, в соответствии с принципом произведения, сразу получаем этот результат.
2.5. Сочетания.
Пусть имеется множество, состоящее из n одинаковых элементов. Каждое его подмножество, содержащее к элементов, называется сочетанием из n элементов по к. Число сочетаний из n элементов по к обозначают 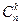 (от французского слова combinaison, что и означает сочетание) и вычисляют по формуле:
(от французского слова combinaison, что и означает сочетание) и вычисляют по формуле: 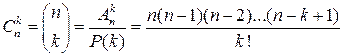 или
или 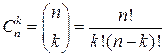 .
. 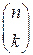 читается, как энка. Получить эту формулу можно так: из n различных элементов по k можно составить
читается, как энка. Получить эту формулу можно так: из n различных элементов по k можно составить 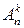 размещений. Если элементы одинаковы, то число
размещений. Если элементы одинаковы, то число 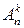 разделим на число перестановок из k , т. е. Р(k). Числа
разделим на число перестановок из k , т. е. Р(k). Числа 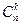 называются также биномиальными коэффициентами, так как они являются коэффициентами в разложении бинома Ньютона, определяющего результат возведения бинома (а + b) в n-ю степень и имеющего вид
называются также биномиальными коэффициентами, так как они являются коэффициентами в разложении бинома Ньютона, определяющего результат возведения бинома (а + b) в n-ю степень и имеющего вид
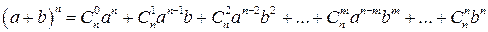 или
или 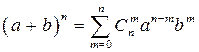 .
.
Пример. Сколькими способами можно выбрать 3 яблока из 5? (Искомое число способов равно числу трехэлементных подмножеств множества из 5 элементов:
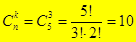 )
)
Пример. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек? (Чтобы рассмотреть все возможные комиссии, нужно рассмотреть все возможные 3-элементные подмножества множества, состоящего из 7 человек. Искомое число способов равно 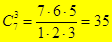 ).
).
Пример. В турнире принимали участие n шахматистов, и каждые 2 шахматиста встретились 1 раз. Сколько партий было сыграно в турнире? ( Партий было сыграно столько, сколько можно выделить 2-элементных подмножеств в множестве из n элементов, т. е. 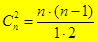 )
)
2.6. Свойства сочетаний. Формула бинома Ньютона.
1. 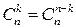 . Очевидно, что число способов, которыми можно выбрать k элементов из n совпадает с числом способов, которыми можно не выбрать n -k элементов из n. Легко проверяется непосредственным вычислением, выражая число комбинаций через факториалы.)
. Очевидно, что число способов, которыми можно выбрать k элементов из n совпадает с числом способов, которыми можно не выбрать n -k элементов из n. Легко проверяется непосредственным вычислением, выражая число комбинаций через факториалы.)
Пример. Сколькими способами можно попасть из левого нижнего угла таблицы в правый верхний, если передвигаться можно только по рёбрам клеток? Каждый кратчайший путь из точки (0; 0) в точку (m; n) состоит из (m + n)отрезков, причем среди них есть m горизонтальных и n вертикальных отрезков. Разные пути отличаются лишь порядком чередования горизонтальных и вертикальных отрезков. Поэтому общее число путей равно числу способов, которыми из (m + n)отрезков можно выбрать nвертикальных отрезков, т. е. 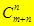 .
.
Можно было бы рассматривать число способов выбора не n вертикальных, а m горизонтальных отрезков, и мы получили бы тогда ответ 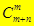 . Итак,
. Итак, 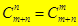 .
.
Итак, число кратчайших путей из точки (0; 0) в точку (m,n) равно 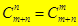 .
.
2. 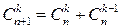 или
или 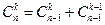 . Первая формула получается так: Рассмотрим группу из n+1 человек. Нас интересует, сколькими способами можно составить из них команду из k человек. Зафиксируем одного из них и обозначим его А. Разобьём все возможные команды на две группы: те, в которые А входит и те, в которые нет. Число команд в первой группе равно
. Первая формула получается так: Рассмотрим группу из n+1 человек. Нас интересует, сколькими способами можно составить из них команду из k человек. Зафиксируем одного из них и обозначим его А. Разобьём все возможные команды на две группы: те, в которые А входит и те, в которые нет. Число команд в первой группе равно 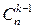 - k- тый здесь А. Число команд во второй группе равно
- k- тый здесь А. Число команд во второй группе равно 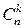 - здесь нет А. Тогда общее число команд и будет
- здесь нет А. Тогда общее число команд и будет 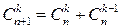 .Можно рассуждать иначе: В предыдущем примере правый верхний угол обозначим А(k,n-k). Попасть в него можно только или из точки А1(k-1,n-k)
.Можно рассуждать иначе: В предыдущем примере правый верхний угол обозначим А(k,n-k). Попасть в него можно только или из точки А1(k-1,n-k) 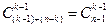 способами или из точки А2(k,n-k-1)
способами или из точки А2(k,n-k-1) 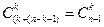 способами. Сумма
способами. Сумма
этих двух выражений и даст второе представление искомой формулы.
3. Число всех подмножеств множества из n элементов равно 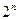 .
.
(Пронумеруем элементы множества и для каждого подмножества множества построим последовательность длины n из нулей и единиц по следующему правилу: если элемент с номером k входит в подмножество на k-м месте пишем 1, а если элемент с номером k не входит в подмножество, то пишем 0. Итак, каждому подмножеству соответствует своя последовательность нулей и единиц. Например, пустому множеству соответствует последовательность из одних нулей. Число всех возможных последовательностей длины n, составленных из нулей и единиц, равно, согласно принципу умножения, 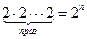 .Следовательно, и число всех подмножеств исходного множества равно
.Следовательно, и число всех подмножеств исходного множества равно 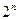 .)
.)
Так как 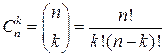 - это число к-элементных подмножеств множества из n элементов, то
- это число к-элементных подмножеств множества из n элементов, то 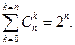
3. Методы решения комбинаторных задач.
При решении конкретной задачи надо выяснить, не решается ли она непосредственно применением принципов комбинаторики. Если нет, то следует выяснить, какие именно подмножества следует рассматривать, допустимы или нет повторения элементов.
1. Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие две женщины не сидели рядом? (По условию, места, занятые мужчинами и женщинами чередуются. Ha 5 местах женщин можно посадить 5! способами. Аналогично, на оставшихся 5 местах 5 мужчин можно посадить 5! способами. По правилу произведения получаем (5!)2 различных способов рассадки. Пoменяв местами мужчин и женщин, получаем eщё (5!)2 способов рассадки. Следовательно, условию задачи удовлетворяют 2(5!)2 способов.)
2.В городе живёт 30000 жителей. Доказать, что, по крайней мере, у двоих из них имя, отчество и фамилия начинаются с одинаковых букв. (В русском алфавите 33 буквы, но по крайней мере с букв Ь и Ъ русские слова не начинаются. Поэтому общее число разных инициалов не больше 313=29791, то есть меньше 30000.) 3. Из города А в город В ведут 7 дорог, а из города В в город С- 4 дороги. Сколькими способами можно проехать из А в С через В? (Каждый путь искомого вида задается парой (а, Ь), где а- один из путей, соединяющих А и В, а b- один из путей, соединяющих В и С. Так как по условию а можно выбрать семью способами, а b- четырьмя, то пару (а, b) по правилу произведения можно выбрать 7• 4= 28 способами.) 4.Сколько 4-хзначных чисел, делящихся на 4, можно составить из цифр 1, 2, 3, 4, 5? (Первые 2 цифры можно выбрать 5 способами, а последние 2 – это только 12, 24, 32, 44, 52. Таким образом, всего способов 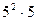 =125)
=125)
5.Код кейса состоит из 6 цифр. На набор одной цифры уходит одна минута. Сколько времени потребуется вору для вскрытия кейса?
6.11 депутатов должны выбрать своего председателя, его заместителя, мэра города, его заместителя и козла отпущения. Сколькими способами это можно сделать?
7.Сколько различных слов можно составить путем перестановки букв из слов МАТЕМАТИКА, ФИЗИКА, ИНФОРМАТИКА, РАДИО,ЭКОНОМИКА?
8.Сколькими способами можно расставить n человек в одной очереди?
9.Сколькими способами можно разместить k студентов одной аудитории на n мест (n>k)?
9.Сколькими способами можно разместить k студентов одной аудитории на n мест (n>k)?
10.Сколькими способами можно заполнить k мест в одной аудитории на n мест (n>k)?
11.Сколько существует пятизначных чисел, в записи которых есть хотя бы две одинаковые цифры? (Всего пятизначных чисел 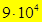 так как 1-я цифра не ноль. Если все цифры разные, то 1-ю и 2-ю цифры выбирают 9 способами, 3-ю-8, 4-ю-7, 5-ю-6 способов, то есть
так как 1-я цифра не ноль. Если все цифры разные, то 1-ю и 2-ю цифры выбирают 9 способами, 3-ю-8, 4-ю-7, 5-ю-6 способов, то есть 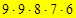 способов. Таким образом, пятизначных чисел, в записи которых есть хотя бы две одинаковые цифры
способов. Таким образом, пятизначных чисел, в записи которых есть хотя бы две одинаковые цифры 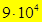 -
- 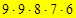 .)
.)
12.Сколькими способами можно поставить на шахматную доску белyю и чёрную ладью так, чтобы они не били друг друга? (Поле для белой ладьи можно выбрать 64 способами. Независимо от этого выбора, ладья бьёт 14 полей и стоит на одном, поэтомy для черной ладьи остается 64 - 15= 49 пoлей)
13. Сколькими способами можно распределить 20 различных конфет между пятью детьми так, чтобы каждый ребёнок получил 4 конфеты? (Для 1-го 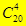 способов, для 2-го уже
способов, для 2-го уже 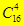 , для 3-го-
, для 3-го- 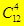 , для 4-го
, для 4-го 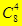 , для 5-го
, для 5-го 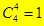 .
.
14. Сколькими способами можно распределить n одинаковых шаров по k ящикам так, чтобы не было пустых. (Пусть все n шаров- на полке, а распределение на к групп осуществляется установкой (к-1) перегородок. Чтобы не было пустых ящиков, перегородка стоит между двумя шарами, а таких промежутков (n-1). Таким образом, выбор можно сделать 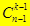 способами)
способами)
15.Сколько шестизначных чисел, кратных пяти, можно составить из цифр: 1,2,…9, если каждую цифру можно использовать несколько раз.) (Последняя цифра 5, то есть 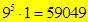 .)
.)
16.Сколько шестизначных чисел, кратных пяти, можно составить из цифр: 0,1,2,…9, если каждую цифру можно использовать несколько раз. (Последняя цифра 0 или 5. Таким образом, для первой цифры – 9 способов ( она не 0), для следующих четырёх - 10 способов, для последней цифры – два способа, то есть 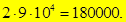 )
)
17.Сколько шестизначных чисел, кратных пяти, можно составить из цифр: 1,2,…9, если каждую цифру можно использовать только один раз? ( Последняя цифра 5, то есть 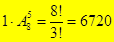 )
)
18.Сколько шестизначных чисел, кратных пяти, можно составить из цифр: 0,1,2,…9, если каждую цифру можно использовать только один раз? (Последняя цифра 5, первая не 0, 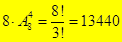 , последняя цифра 0,
, последняя цифра 0, 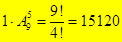 , то есть
, то есть 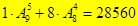 .
.
19. В урне7 шаров: 3 белых и 4 чёрных. а) Вынимают один шар. Найти вероятность вынуть белый. б) Вынимают два шара. Найти вероятность вынуть: два белых, ни одного белого. а) Обозначим через А – вытягивание белого шара, N=7 – число всех случаев; M=4 – число случаев, благоприятствующих событию А. Тогда P(A) = 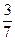 . б) Число благоприятных исходов – это число способов, которыми можно вынуть два белых шара из трёх, то есть
. б) Число благоприятных исходов – это число способов, которыми можно вынуть два белых шара из трёх, то есть 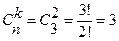 . Общее число исходов - это число способов, которыми можно вынуть два белых шара из семи, то есть
. Общее число исходов - это число способов, которыми можно вынуть два белых шара из семи, то есть 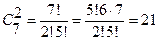 .
.
20.Какова вероятность появления герба, по крайней мере, один раз при двукратном бросании монеты? Пространство равновозможных элементарных событий данного опыта состоит из следующих событий: 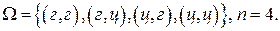 Событие
Событие 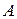 , состоящее в том, что при двукратном бросании монеты герб появится, по крайней мере, один раз, происходит при появлении одного из несовместных элементарных событий
, состоящее в том, что при двукратном бросании монеты герб появится, по крайней мере, один раз, происходит при появлении одного из несовместных элементарных событий 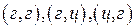 . Следовательно,
. Следовательно, 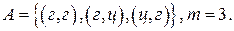 Таким образом,
Таким образом, 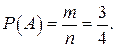
21. Технический контроль проверяет из партии в 500 деталей 20 деталей, взятых наудачу. Партия содержит 15 нестандартных деталей. Какова вероятность того, что среди проверяемых деталей будет ровно две нестандартные?Так как по условию задачи 20 деталей из 500 извлекаются наудачу, то все возможные варианты извлечения 20 деталей из 500 естественно считать равновозможными и для нахождения требуемой вероятности воспользоваться классической схемой (классическим определением вероятности).Так как порядок следования стандартных и нестандартных деталей в извлекаемых 20 не играет роли, а играет роль только количество стандартных и нестандартных деталей, то количество всех возможных способов, которыми это можно сделать, равно 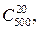 то есть
то есть 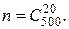 Событию
Событию 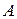 , состоящему в том, что будут извлечены две нестандартные детали при извлечении 20 (следовательно, остальные 18 должны быть стандартными), будет соответствовать
, состоящему в том, что будут извлечены две нестандартные детали при извлечении 20 (следовательно, остальные 18 должны быть стандартными), будет соответствовать 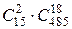 исходов, то есть
исходов, то есть 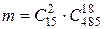 . Таким образом,
. Таким образом, 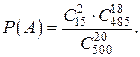
22.Трехзначное число составляется следующим образом: бросаются три игральные кости: белая, синяя и красная; число выпавших очков на белой кости – это число сотен, число выпавших очков на синей кости – это число десятков, а число выпавших очков на красной кости – это число единиц трехзначного числа. Какова вероятность того, что полученное таким образом число будет больше 456? Количество всех чисел, которые можно получить указанным способом – это число размещений с повторениями из 6 по 3. Следовательно, 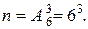

Числа большие 456 будут получаться, если число сотен будет больше 4, то есть 5 или 6 или число сотен будет равно 4, а число десятков будет больше чем 5, то есть 6. Количество таких чисел будет 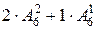 . Следовательно,
. Следовательно, 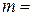
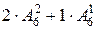 =
= 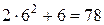 и
и
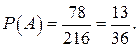
Пример. В партии из N одинаковых деталей M бракованных. Выбирается (не возвращая) n деталей. Какова вероятность того, что среди них окажется ровно m бракованных? Общее количество случаев (сочетания из N деталей по n) равно 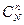 . Мы выбираем m бракованных деталей среди M бракованных, но и одновременно выбираем (n-m) деталей без брака среди N-M деталей без брака. Тогда, по основному принципу комбинаторики, такому выбору благоприятствует
. Мы выбираем m бракованных деталей среди M бракованных, но и одновременно выбираем (n-m) деталей без брака среди N-M деталей без брака. Тогда, по основному принципу комбинаторики, такому выбору благоприятствует 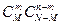 случаев. Поэтому искомая вероятность равна
случаев. Поэтому искомая вероятность равна 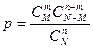
1.2 Действия над событиями
Определение 1. Если всякий раз, когда происходит событие А, происходит и событие В, то говорят, что событие А влечет за собой событие В, 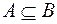 (рис.1)
(рис.1)
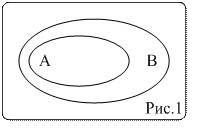
Определение 2. Говорят, что два события А и В равны (А=В) тогда и только тогда, когда 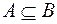 и
и 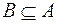 .
.
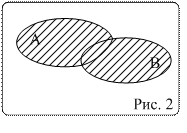
Определение 3. Под суммой двух событий А и В будем понимать такое событие С (С=А+В), которое состоит либо в появлении события А, либо в появлении события В ( рис.2).
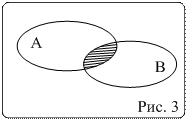
Определение 4. Под произведением двух событий А и В будем понимать такое событие С ( 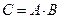 ), которое состоит в одновременном появлении и события А, и события В ( рис.3).
), которое состоит в одновременном появлении и события А, и события В ( рис.3).
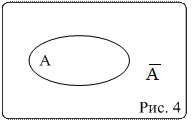
Определение 5. Событие 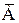 , противоположно событию А, если
, противоположно событию А, если 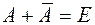 и
и 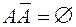 ( рис. 4).
( рис. 4).
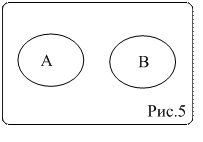
Определение 6. Два события называются несовместными, если они одновременно произойти не могут ( рис.5). Два события несовместны, если АВ=Ø.
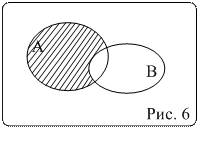
Определение 7. Событие, состоящее в том, что событие А произошло, а событие В не произошло, обозначается А-В=А-АВ ( рис. 6).
Определение 9. Два события называются зависимыми, если вероятность одного события зависит от появлении или непоявления другого.
Определение 8. Два события называются независимыми, если вероятность одного события не зависит от появления или непоявления другого.
Определение 10. Двасобытия А и В будем называть совместными, если каждое из них содержит хотя бы одно общее элементарное событие, т.е если АВ 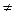 Ø и несовместными, если АВ = Ø.
Ø и несовместными, если АВ = Ø.
Пример. А – выбор червонной карты и В – выбор десятки – совместные события, так как
АВ = выбор червонной десятки 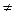 Ø
Ø
Пример. А – выпадение четного числа очков А = {2, 4, 6}. В – выпадение нечетного числа очков В = {1, 3, 5}. Очевидно, что А и В несовместны.
Определение 11. Полная группа событий – это совокупность n событий А1, А2, …, Аn, одно из которых обязательно произойдет, т.е. 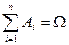
Дата добавления: 2016-07-27; просмотров: 7772;











