Определение кинетических констант сложных реакций методами нелинейного программирования.

Рассмотренные выше схемы реакций ограничивают возможности определения кинетических констант по экспериментальным данным, полученным в интегральном реакторе. Для более сложных реакционных схем, когда нет возможности получить интегральное решение кинетических уравнений, связывающее в явном виде константы скорости и время с текущими значениями концентраций реагентов, применяют другие методы определения констант скоростей реакций. Эти методы основаны на использовании метода наименьших квадратов при формулировке условий нахождения констант и метода нелинейного программирования при поиске констант. Рассмотрим эту процедуру поиска на примере определения констант скорости для системы последовательных реакций по экспериментальным данным, полученным в интегральном реакторе периодического действия в режиме линейного нагрева.

Реакции протекают в соответствии со следующей схемой:

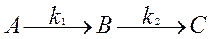(4.3.1)

Скорость процесса описывается следующей системой дифференциальных уравнений:

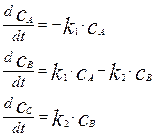(4.3.2)

В результате проведения экспериментов в аппарате периодического действия были получены экспериментальные данные в следующем виде:

Рис.4.3.1. Изменение температуры в процессе эксперимента

Рис.4.3.2. Изменение концентраций реагентов в ходе эксперимента.

Поскольку у нас имеет место неизотермический интегральный эксперимент, то мы должны учитывать температурную зависимость констант скорости.

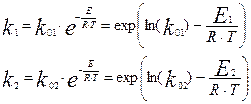(4.3.3)

Кинетическими параметрами, подлежащими определению для данной задачи, являются предэкспоненциальные множители и энергии активации. Сформулируем задачу нахождения кинетических параметров следующим образом: Найти такой набор кинетических параметров, который обеспечивает минимальное значение функции рассогласования между экспериментальными и расчетными данными

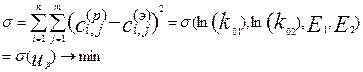(4.3.4)

Процедура поиска минимума функции рассогласования осуществляется следующим образом:

1. Задаются некоторым начальным приближением искомых параметров u_p⁽⁰⁾.

2. Вычисляется градиент функции рассогласования по искомым параметрам:

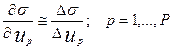(4.3.5)

3. Далее изменяют искомые параметры в соответствии со следующим алгоритмом:

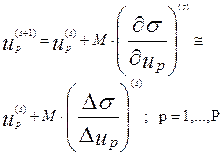(4.3.6)

где s-номер шага поиска, М –коэффициент пропорциональности изменения параметра в направлении градиента минимизируемой функции. При градиентном методе параметры изменяются на каждом шаге поиска в направлении градиента, однако, этот метод требует большого объема вычислений, связанных с необходимостью вычисления градиента функции в каждой точке поиска. Для сокращения объема вычислений применяют обычно так называемый метод наискорейшего спуска.

При использовании этого метода после каждого шага по направлению к экстремуму, проверяется, удачным ли был этот шаг:

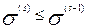(4.3.7)

Если условие (4.3.7) выполняется, то следующий (s+1)-й шаг делается в этом же направлении, если же (4.3.7) не выполняется, то делается возврат в предыдущую точку, вычисляется новое значение градиента и делается шаг с новым значением градиента.

На следующих рисунках показаны результаты использования описанной процедуры для поиска констант скорости последовательных реакций по экспериментальным данным, приведенным выше. На рисунке 4.3.3 показано описание экспериментальных данных при начальном приближении кинетических параметров, указанных на рисунке.

Рис.4.3.3. Описание экспериментальных данных при начальном приближении кинетических параметров, приведенных на рисунке. Остаточная сумма квадратов отклонений s =2504.3

. После 13 шагов достигается минимум, и величина функции рассогласования становится очень маленькой величиной и совпадение между расчетными и экспериментальными данными практически полное.

Рис. 4.11. Описание экспериментальных данных после нахождения минимума функции рассогласования. Точка минимума была достигнута через 13 шагов. Остаточная сумма отклонений 1×10^-17

С помощью описанной процедуры и при использовании специального программного комплекса ReactOp можно решать задачи поиска кинетических параметров для схем любой сложности для экспериментальных данных, полученных как в интегральном, так и в дифференциальном реакторах.