Обработка результатов косвенных измерений.

Пусть косвенное измерение у связано с т прямыми измерениями известной зависимостью:

,

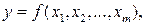причем каждое из них проведено п раз.

Очевидно, т погрешностей, например, первого измерения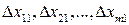
вызовут определенную погрешность косвенного из­мерения 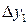. Обычно величины 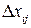весьма малы, а прямые измерения x_i можно считать независимыми. Тогда связь прямых
и косвенных погрешностей в первом измерении определяется из­вестным выражением полного дифференциала функции несколь­ких переменных: 1г

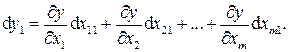(27.20)

Аналогичные выражения можно записать и для остальных п из­мерений:

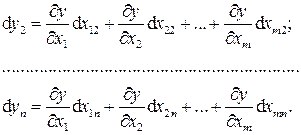(27.21)

Возведем эти выражения в квадрат, пренебрегая смешанными членами типа dx_ijdx_ki, и разделим на (п - 1).

Тогда в левой части получим квадрат среднего квадратичного отклонения косвенного измерения, в правой части, после простых преобразований, - со­ответствующие параметры прямых измерений:

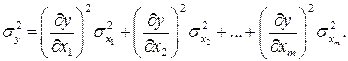(27.22)

Аналогичную связь можно получить и между другими парамет­рами точности прямых и косвенных измерений.

Найдем, например, погрешность среднеарифметического, рас­сматривая его как косвенное, а Х₁, Х₂, ..., Х_N как прямые с одина­ковым средним квадратичным отклонением σ. Их связь дается выражением:

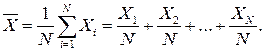(27.23)

Но 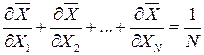и в соответствии с (27.22) получаем:

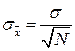. (27.24)

Часто встречается случай, когда косвенное измерение представ­ляет произведение или частное прямых измерений. Например, при определении плотности вещества цилиндра

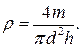(27.25)

Найдем соответствующие производные

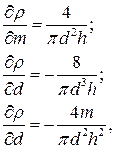(27.26)

подставим их в (1) и разделим на (2):

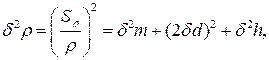(27.27)

где 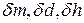- относительные погрешности прямого изме­рения массы, диаметра и высоты цилиндра.

Таким образом, если косвенное измерение представляет собой частное и произведение прямых, то следует складывать квадраты не средних квадратичных отклонений σ², а относительных погреш­ностей δ², причем коэффициент перед относительной погрешностью, равен показателю степени соответствующего прямого измерения (см. формулы (27.25), (27.27).