Методы измерений. Понятия и классификация.
Метод измерений – совокупность приемов, обеспечивающих сравнение измеряемой физической величины с её единицей (мерой).
Методы измерений основаны на физических принципах взаимодействия объекта измерения и средств измерения для получения измерительной информации с допустимой погрешностью.
Методы измерений различают:
1) по физическому принципу измерения (механические, пневматические, акустические, оптические, электрические и т.п.);
2) по виду измерительных сигналов в средствах измерения (аналоговые (соответствующая функция непрерывна) и цифровые (функция квантуется));
3) по способу сопоставления измеряемой физической величины и меры, различают метод непосредственной оценки и методы сравнения.
Наиболее распространен метод непосредственной оценки, в нем о физической величине судят по показаниям одного (прямые измерения) или нескольких (косвенные измерения) приборов, которые заранее проградуированы в единицах измеряемой величины.
В методах сравнения измеряемая величина сопоставляется с мерой, которая находится вне средств измерения.
Различают дифференциальный метод, где об измеряемой величине судят по её разности с каким-либо эталоном.
Рассмотрим U-образный жидкостный манометр, измеряемой величиной является давление Px (рис. 88).
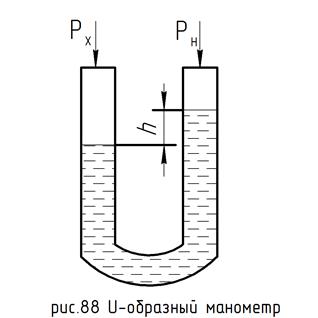
Давление Px находится по формуле:
Px=PH+ρgh. (27.6)
Если Px>PH, то соответствующая жидкость выдавливается в трубку, соединенную с мерой (эталоном).
В дифференциальных методах мы предполагаем, что эталон, с которым сравнивается измеряемая величина, находится более точно, чем сама величина - Px, поэтому ошибка будет заложена в измерении ρgh, а точнее, т. к. довольно точно известны плотность и ускорение свободного падения, то вся погрешность располагается в измерении высоты - h, и чем, больше эта высота, тем меньше погрешность.
Разность между Px и PH должна быть как можно меньше, следовательно, высоту h нужно увеличить, например при измерении давления в камере сгорания ракетного двигателя это достигается с помощью уменьшения плотности - ρ - вместо воды используется масло, или наклона плеча пьезометр, если погрешность измерения высоты составляет примерно 1 мм при наличии трубки высотой в 1,5 м, то погрешность будет 1мм/1500. В настоящее время давление окружающей среды - PH измеряется с высокой точностью, поэтому дифференциальный метод позволяет значительно более точно измерить давление Px , чем прямым образом, т. е. с использованием манометра.
Разновидностью дифференциального вида является нулевой метод, когда средство измерения при нагружении его измеряемой величиной возвращается в исходное положение.
В рассматриваемом примере величина ρgh→0, т. к. h=0. Гистерезис отсутствует, левое плечо столба уходит в правое, из - за поверхностного натяжения жидкость остается на стенках и, естественно, что показания прибора искажаются, если уравновесить давление Px, т. е. давление PH заменить переменным давлением, которое можно достаточно точно измерить, то столбики вернутся в исходное положение, и параметры диссипации энергии будут отсутствовать.
Нулевой метод более точный, т. к. погрешность сосредоточена преимущественно в эталоне, т. е. какова погрешность эталона, такова и погрешность данного метода.
В методе замещения об измеряемой величине судят по изменению измерительного сигнала при замене объекта измерения эталоном.
Рассмотрим нагруженный динамометр, который проградуирован в единицах массы (рис. 89).
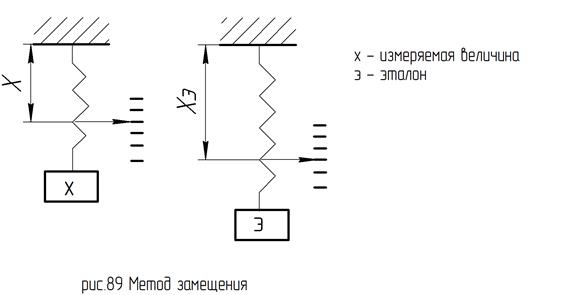
Вместо измеряемой величины нагружаем средство измерения эталоном.
Об измеряемой величине судим по соотношению:
X / Xэ,
чем ближе эталон к измеряемой величине, тем точнее будет измерение.
В методе совпадений разность между измеряемой величиной и воспроизводимой мерой определяется с помощью совпадения каких – либо периодических сигналов, например отметок шкалы (штангенциркуль).
§ 27.7. Погрешность и точность измерений. Основные понятия. Виды погрешностей измерений.
Погрешность измерения - разность между измеряемой ( 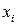 ) и идеальной (
) и идеальной ( 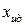 ) величинами.
) величинами.
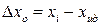 , (27.7)
, (27.7)
т. К. Значение идеальной величины нам неизвестно, то воспользуемся понятием действительной погрешности:
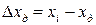 , (27.8)
, (27.8)
где
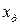 - величина, определяемая с максимальной точностью возможной в данном измерении.
- величина, определяемая с максимальной точностью возможной в данном измерении.
Точным прибором не пользуются в непосредственных практических измерениях, в частности при измерении давления в камере сгорания можно воспользоваться поршневым манометром, позволяющим с высокой степенью точности определить давление, но он осуществляет длительный замер в статических условиях, поэтому используют пьезометрический датчик, который ставят на плечо прибора, и показания градуируется с помощью поршневого манометра, тем самым находится действительная величина давления, следовательно, можно определить действительную погрешность, а значение измеряемой величины считывают по показаниям другого манометра или датчика.
Различают по месту возникновения в измерительной цепи объективные и субъективные погрешности.
К объективным относятся:
1) инструментальные (смещение стрелки прибора шкалы и т.п.);
2) установочные (негоризонтальность, непараллельность и т.п.);
3) погрешность метода измерения (измерение температуры движущейся среды термопарой с открытым спаем) – самые тяжелые, для их ликвидации требуется глубокое знание механических процессов ;
4) теоретические – при измерении реальный объект измерения заменяется некой моделью, е. Модель будет неправильно сформирована, то будут совершаться методические, теоретические ошибки. Например, необходимо найти площадь критического сечения ракетного двигателя, мы предполагаем, что оно имеет простую форму, но после его измерения запускается двигатель, сопло нагревается, из – за температурных и пластических деформаций приобретает другую форму, и площадь критического сечения уже трудно измерить.
Субъективные погрешности связаны со свойствами наблюдателя (динамические характеристики).
По влиянию помех (неизменяемые величины) различают основную и дополнительную погрешность.
В паспорте прибора приводится диапазон этих величин (давление, температура окружающей среды и т.д.), в рамках которого погрешность измерения не превышает заданную величину. В ряде случаев предусматривается область расширения этого диапазона, вызывающая соответствующую дополнительную погрешность (например, температурная погрешность).
Если в паспорте не указывается область, то существуют методы, позволяющие оценить выходы за ее пределы.
Например, температурная погрешность связана с коэффициентом линейного расширения (α) следующим соотношением:
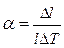 . (27.9)
. (27.9)
Для исключения температурных погрешностей средства и объект измерения должны иметь одинаковую нормальную температуру, равную t0=20° С. Особо точные измерения должны кондиционироваться.
По форме представления различают абсолютную ( 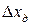 ) и относительную (
) и относительную ( 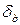 ) погрешности:
) погрешности:
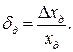 (27.10)
(27.10)
По способу обработки различают случайные и систематические погрешности, последние могут быть исключены с помощью поправок.
Рассмотрим точный поршневой (образцовое средство измерения) и обычный стрелочный (рабочее средство измерения) манометры, которые нагружаются одинаковым давлением – Pх.

Измерения проводится в нескольких точках, в каждой по несколько раз. Получают следующие погрешности Δx по измеряемой величине.
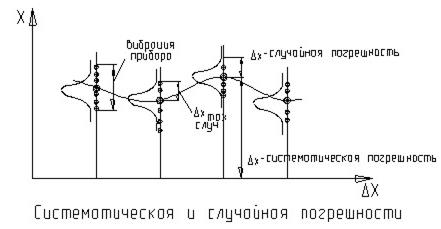
Внутри диапазона в нескольких точках снимаются показания рабочего манометра, каждый раз образцовое средство измерения загружается опять повторно.
Измерения одной и той же величины в одних и тех же условиях - повторные.
Точки - результаты повторных опытов, их может быть достаточно большое количество. Распределением Гаусса можно пользоваться не менее чем при 30 измерениях, иначе используется критерий Стьюдента.
Возьмем хобр - значение, которое показывает образцовое средство измерения. Величину погрешности можно найти, сравнивая показания прибора с образцовым:
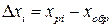 . (27.11)
. (27.11)
Выполняя обработку прямых результатов измерения, определим остальные параметры распределения.
Первый статистический параметр измерения - математическое ожидание:
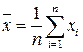 . (27.12)
. (27.12)
Множество случайных погрешностей измерения:
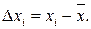 (27.13)
(27.13)
Среднее квадратичное отклонение:
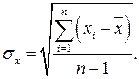 (27.14)
(27.14)
В результате мы можем построить распределение вокруг какой-либо точки - математического ожидания.
Отклонение математического ожидания от действительного значения измеряемой величины представляет собой систематическую составляющую погрешности:
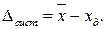 (27.15)
(27.15)
Отклонение единичных повторных измерений от математического ожидания - случайная составляющая погрешности:
Разброс случайных погрешностей относительно математического ожидания характеризуется вариацией средства измерения.
§ 27.8. Обработка результатов измерений. Однократные и многократные измерения. Исключение грубых и систематических погрешностей измерений. Оценка случайной составляющей погрешности измерений.
Алгоритм.
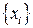 - множество случайных результатов измерения (повторные опыты, из которых исключена систематическая составляющая погрешности измерения).
- множество случайных результатов измерения (повторные опыты, из которых исключена систематическая составляющая погрешности измерения).
С помощью формулы (27.12) находится математическое ожидание, используя уравнение (27.13) - множество случайных погрешностей измерений, с помощью формулы (27.14) – величина среднего квадратичного отклонения и исключаются промахи:
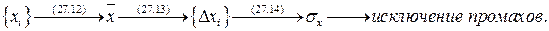
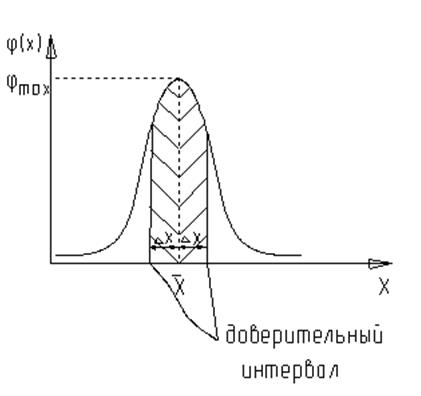
На графике изображены результаты повторных опытов. После построения гистограммы или математической обработки наносится соответствующая кривая распределения Гаусса, максимум которой находится в точке соответствующей математическому ожиданию, вид кривой определяется двумя статическими параметрами – математическим ожиданиям и средним квадратичным отклонением.
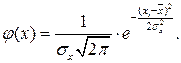 (27.16)
(27.16)
Зная кривую, можно найти вероятность появления некоторого измерения в каком - либо интервале, в отличие от других измерений, вводится понятие доверительного интервала, который является симметричным относительно математического ожидания и относительного его определяется доверительная вероятность. Функция Гаусса четная, следовательно, можно определить вероятность появления результата единичного измерения в интервале, равного удвоенной функции Лапласа от квантиля нормального распределения:
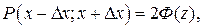 (27.17)
(27.17)
квантиль
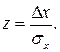 (27.18)
(27.18)
В технических измерениях в качестве доверительной вероятности обычно используется величина 0,95, что соответствует удвоенному квантилю нормального распределения:
z = 2,
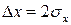 ,
,
P(2)=0,95.
Иногда используется коэффициент значимости, равный разности между единицей и доверительной вероятностью
Интервал Δx называется в этом случае – доверительным, а вероятность - доверительная вероятность.
Пусть было проведено 1000 измерений, выбрана вероятность 0,95, необходимо определить промахи в данном множестве х. Закономерно, что 950 измерений лежат внутри доверительного интервала, а 50 могут быть за пределами, те измерения, которые попали за пределами доверительного интервала, являются закономерными для того количества измерений. При 100 измерениях 95 должны входить в интервал, при 10 измерениях за пределами может лежать одно рядом с границами интервала, либо ничего. Чем дальше измерения отклоняются от математического ожидания, тем меньше вероятность его появления, и тем больше вероятность того, что это измерение - промах,.
Для проверки на промах из всего множества случайных величин выбирается результат, имеющий максимальное отклонение от математического ожидания - 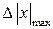 , находится его квантиль -
, находится его квантиль - 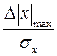 , которое если не превышает критерия Шовена S(n), зависящего от числа измерений, то результат не считается промахом:
, которое если не превышает критерия Шовена S(n), зависящего от числа измерений, то результат не считается промахом:
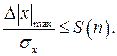 (27.19)
(27.19)
Если условие не выполняется, то результат этого измерения исключается, и обработка повторяется с новыми значениями 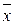 , до тех пор, пока все промахи не будут исключены. Затем результат измерения записывается в форме:
, до тех пор, пока все промахи не будут исключены. Затем результат измерения записывается в форме:
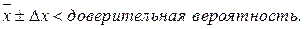
Дата добавления: 2016-07-27; просмотров: 4819;











