Формула полной вероятности и формула Бейеса
Основные понятия теории вероятностей
Теория вероятностей - математическая наука, изучающая закономерности в случайных явлениях. Одним из основных понятий теории вероятности является понятие случайного события (или просто события) Событием называется всякий факт, который в результате опыта (испытания, эксперимента) может произойти или не произойти. Примеры событий: выпадение шестерки при бросании игральной кости; отказ технического устройства за время его работы τ ; искажение сообщения при передаче его по каналу связи. С событиями связываются некоторые числа, характеризующие степень объективной возможности этих событий, называемые вероятностями событий.
К понятию «вероятность» существует несколько подходов. Один из них («классический») основан на подсчете числа исходов опыта, благоприятных данному событию, и его отношения к общему числу равновозможных исходов. Другой подход (так называемый «частотный» или «статистический) основан на понятии частоты события в длинной серии опытов. Частотой события в серии из N опытов называется отношение числа опытов, в которых произошло событие, данное событие, к общему числу произведенных опытов. Существуют случайные явления, в которых наблюдается устойчивость частот; она состоит в том, что при увеличении числа независимых опытов N частота события стабилизируется, приближаясь к какой-то постоянной величине; эта величина и называется вероятностью события.
Современное построение теории вероятностей основывается на аксиоматическом подходе и опирается на элементарные понятия теории множеств.
Основные понятия теории множеств:
Множеством называется любая совокупность объектов произвольной природы, каждый из которых называется элементом множества. Примеры множеств: множество студентов, обучающихся в данном вузе, множество натуральных чисел, не превосходящих 100, множество точек на плоскости, лежащих внутри или на границе круга с радиусом единица и центром в начале координат.
Множество обозначается по разному: одной большой буквой; перечислением его элементов, данным в фигурных скобках; указанием в фигурных скобках правила, по которому элемент относится к множеству. Например, множество М натуральных чисел от 1 до 100 может быть записано в виде
M={1,2,…..100} = {i- целое; 1 ≤ i ≤ 100}.
По числу элементов множества делятся на конечные и бесконечные. Конечное множество может, в частности, состоять из одного элемента. Бесконечное множество называется счетным, если все его члены можно пересчитать в определенной последовательности. Например множество всех натуральных чисел = бесконечное, счетное множество. Множество точек внутри круга является бесконечным и несчетным (его элементы нельзя перенумеровать.
Два множества А и В совпадают или эквивалентны, если они состоят из одних и тех же элементов (обозначается А=В).
Запись а 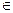 А означает: объект А является элементом множества А; или а принадлежит А. Запись
А означает: объект А является элементом множества А; или а принадлежит А. Запись 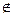 А означает: объект а не является элементом множества А.
А означает: объект а не является элементом множества А.
Пустым множеством называется множество, не содержащее ни одного элемента.; оно обозначается  0. Все пустые множества эквивалентны друг другу.
0. Все пустые множества эквивалентны друг другу.
Множество В называется подмножеством (частью множества А , если все элементы В содержатся также и в А; обозначение В 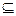 А или А
А или А 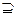 В. Считается, что пустое множество является частью любого множества А:
В. Считается, что пустое множество является частью любого множества А: 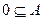 .
.
Объединением (суммой множеств А и В) называется множество С = А+В, состоящее из всех элементов А и всех элементов В (в том числе и тех, которые принадлежат и А и В. Объединение двух множеств = это совокупность элементов принадлежащих хотя бы одному из них.
Аналогично определяется объединение любого числа множеств:
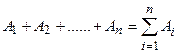
Рассматриваются объединения бесконечного (счетного) числа множеств
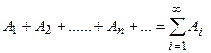
Пересечением (произведением) множеств А и В называется множество D = A∙B. Аналогично определяется пересечение любого числа множеств. Множество 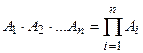 состоит из элементов , входящих одновременно во все А1,А2,…Аn . Определение распространяется и на бесконечное (счетное) число множеств.
состоит из элементов , входящих одновременно во все А1,А2,…Аn . Определение распространяется и на бесконечное (счетное) число множеств.
Множества А и В называются непересекающимся, если их пересечение есть пустое множество. А ∙В = 0, т.е. нет ни одного элемента, входящего и в А и в В. Также как при записи обычного умножения знак ∙ в произведении часто опускается.
Этих элементарных сведений по теории множеств достаточно для того, чтобы что бы пользоваться схемой теоретико- множественной схемой построения теории вероятностей.
Пусть производится некоторый опыт (эксперимент), результат которого заранее неизвестен, случаен. Рассмотрим множество Ω всех возможных исходов опыта: каждый его элемент 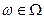 (один отдельный исход опыта) называют элементарным событием., а все множество Ω – пространством элементарных событий. Подмножества множества Ω называются событиями или случайными событиями; любое событие А это подмножество множества Ω:
(один отдельный исход опыта) называют элементарным событием., а все множество Ω – пространством элементарных событий. Подмножества множества Ω называются событиями или случайными событиями; любое событие А это подмножество множества Ω: 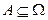 .
.
Пример: опыт состоит в бросании игральной кости; пространство элементарных событий Ω= {1,2,3,4,5,6}; событие А – выпадение четного числа очков. А={2,4,6}; 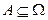 . В частности можно рассматривать событие Ω (ведь каждое множество есть собственное подмножество; оно называется достоверным событием (осуществляется при любом опыте, т.е. наверняка). Ко всему множеству Ω элементарных событий добавляется еще пустое множество ; это множество тоже рассматривается как событие и называется невозможным событием (в результате опыта оно не может произойти
. В частности можно рассматривать событие Ω (ведь каждое множество есть собственное подмножество; оно называется достоверным событием (осуществляется при любом опыте, т.е. наверняка). Ко всему множеству Ω элементарных событий добавляется еще пустое множество ; это множество тоже рассматривается как событие и называется невозможным событием (в результате опыта оно не может произойти
Элементарные события в одном и том же опыте можно задавать по-разному; например при бросании точки на плоскость положение точки можно задавать как парой декартовых координат так и парой.
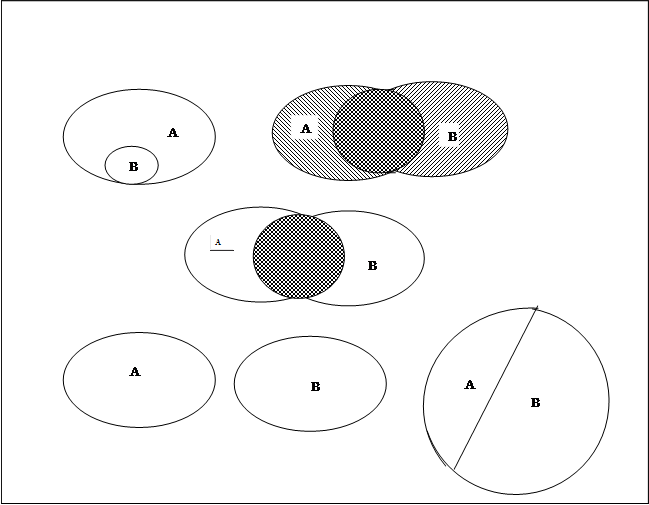
Рис. 3.1
Непересекающиеся события А, В такие что АВ=0 называют несовместными; появление одного из них исключает появление другого. Несколько событий А1, А2, ….,Аn называются попарно несовместными (или просто несовместными) если появление каждого из них исключает появление каждого из остальных.
Несколько событий А1, А2, ….,Аn образуют полную группу, если 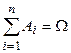 , т.е. их сумма есть достоверное событие (другими словами, в результате опыта обязательно произойдет хотя бы одно из них.
, т.е. их сумма есть достоверное событие (другими словами, в результате опыта обязательно произойдет хотя бы одно из них.
Аксиомы теории вероятностей:
I. Вероятность любого события А заключена между 0 и 1.
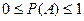
II. Аксиома сложения вероятностей: если А и В несовместные события , то
Р(А+В) = Р(А) + Р(В)
Аксиома обобщается на любое конечное число событий: если А1, А2, ….,Аn – несовместные события, то
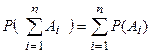
III. Аксиома сложения вероятностей для бесконечной последовательности событий: если А1, А2, ….,Аn, …- несовместные события, то
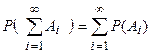
Аксиомы теории вероятностей позволяют вычислять вероятности любых событий (подмножеств пространства Ω) с помощью вероятностей элементарных событий (если их конечное или счетное число).
Для опытов, обладающих симметрией возможных исходов, применяют способ непосредственного вычисления вероятностей событий в так называемой схеме случаев (иначе урн). Этот способ основан на допущении о равновероятности (равновозможности) элементарных событий. Несколько событий А1, А2, ….,Аn называются равновозможными, если в силу симметрии условий опыта относительно этих событий, вероятности их одинаковы:
Р(А1)=Р(А2)= ….=Р(Аn)
Если в какой то опыте пространство элементарных событий Ω можно представить в виде полной группы несовместных и равновозможных событий w1,w2,…wn, то такие события называются случаями (или шансами), а про сам опыт говорят, что он сводится к схеме случаев (схеме урн).
Случай wi называется благоприятным событием А, если он является элементом множества А: 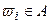 .
.
Так как случаи w1,w2,..,wn образуют полную группу событий то
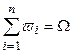 .
.
Так как элементарные события w1,w2,..,wn несовместны , то по аксиоме сложения вероятностей
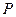
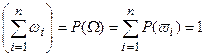
Так как элементарные события w1,w2,..,wn равновозможны , то вероятность каждого из них равна 1/n.
Отсюда непосредственно вытекает так называемая классическая формула для вероятности события: если опыт сводится к схеме случаев, то вероятность события А в этом опыте можно вычислить по формуле
РА(А)=mA/n, где mA – число случаев, благоприятных событию А; n – общее число случаев. Эта формула раньше принималась за определение вероятности.
Пример.
В урне находятся 3 белых и 4 черных шара, тщательно перемешанных. Из урны наугад выбирается один шар. Построить для этого опыта пространство элементарных событий и найти вероятность события А ={вынут белый шар}. Для этого перенумеруем шары в урне номерами от 1 до 7; первые 3 шара белые, последние четыре – черные.
Ω = {1,2,3,4,5,6,7}4 F={1,2,3}/
В силу симметрии условий задачи относительно всех шаров (шар выбирается наугад) элементарные событии равновозможны. Так как они несовместны и образуют полную группу, вероятность события А найдется по формуле РА(А)=mA/n=3/7.
Эта формула дает возможность в некоторых задачах, когда опыт обладает симметрией возможных исходов, непосредственно по условиям опыта вычислять вероятность событий.
Естественным обобщением и расширением непосредственного подсчета вероятностей в схеме случаев является «геометрический подход к вычислению вероятностей событий; он применяется тогда, когда пространство элементарных событий Ω включает несчетное множество элементарных событий 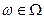 , и по условиям симметрии опыта, никакое из них не имеет преимущества перед другими в смысле возможности появления. ( Мы не говорим, что события равновероятны так вероятность каждого из них равна 0, говорить об этом будем позднее). Пусть пространство элементарных событий Ω – какая то область на плоскости . Если опыт обладает симметрией возможных исходов (например какой-то «точечный» объект «наугад» бросается в пределах области), то все элементарные события «равноправны» и естественно предположить, что вероятности попадания элементарного события w в две области I и II равной площади S а вероятность любого события А
, и по условиям симметрии опыта, никакое из них не имеет преимущества перед другими в смысле возможности появления. ( Мы не говорим, что события равновероятны так вероятность каждого из них равна 0, говорить об этом будем позднее). Пусть пространство элементарных событий Ω – какая то область на плоскости . Если опыт обладает симметрией возможных исходов (например какой-то «точечный» объект «наугад» бросается в пределах области), то все элементарные события «равноправны» и естественно предположить, что вероятности попадания элементарного события w в две области I и II равной площади S а вероятность любого события А 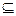 Ω равна отношению площади SA к площади всей области Ω:
Ω равна отношению площади SA к площади всей области Ω:
Р(А) = SA/SΩ.
Эта формула является обобщением классической формулы на несчетное множество событий. Вероятности ,вычисляемые с помощью такого приема называются геометрическими вероятностями.
Формула полной вероятности и формула Бейеса
Если об обстановке опыта можно сделать n исключающих друг друга предположений (гипотез) Н1, Н2,…,Нn и если событие А может появится только вместе с одной из этих гипотез, то
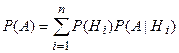 , где Р(Нi) – вероятность гипотезы Нi; P(A|Hi) – условная вероятность события А при этой гипотезе. Формула наз. Формулой полной вероятности
, где Р(Нi) – вероятность гипотезы Нi; P(A|Hi) – условная вероятность события А при этой гипотезе. Формула наз. Формулой полной вероятности
Если до опыта вероятности гипотез Н1, Н2, ….Нn были Р(Н1), Р(Н2), …Р(Нn) , а результате опыта произошло событие А то новые (условные) вероятности гипотез вычисляются по формуле
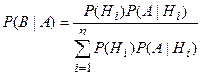 (i=1,2,…,n).
(i=1,2,…,n).
Формула называется формулой Бейеса. Доопытные первоначальные вероятности гипотез Р(Н1), Р(Н2), …Р(Нn) называются априорными, а послеоопытные P(A|Hi) - апостериорными. Формула Бейеса дает возможность «пересмотреть» возможности гипотез с учетом наблюденного результата опыта.
Если после опыта , давшего событие А проводится еще опыт, в результате которого м ожжет произойти или нет событие В, то вероятность (условная) этого последнего события вычисляется по формуле полной вероятности, в которой подставлены не прежние вероятности гипотез Р(Нi) а новые P(Hi|A):
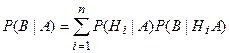
Эту формулу иногда называют формулой будущих событий.
Контрольные вопросы:
1. Написать формулу полной вероятности.
2. Когда применяют формулу Бейеса?
3.4 Дискретные случайные величины
Одним из важнейших понятий теории вероятностей является понятие случайной величины. Под случайной величиной понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение. Примеры; опыт 4 выстрела по мишени; случайная величина – число попаданий; опыт – эксплуатация ЭВМ; случайная величина – время наработки ЭВМ до первого отказа.
При теоретико- множественной трактовке основных понятий теории вероятностей случайная величина Х – это некоторая функция элементарного события ω: Х=φ(ω) где ω 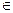 Ω. Значение этой функции зависит от того, какое элементарное событие ω появилось в результате опыта.
Ω. Значение этой функции зависит от того, какое элементарное событие ω появилось в результате опыта.
В дальнейшем случайные величины будем обозначать большими буквами, а неслучайные маленькими.
Законом распределения случайной величины называется любое правило, позволяющее находить вероятности всевозможных событий, связанных со случайной величиной., например вероятность того, что она примет какое-то значение или попадет в какой-то промежуток. Если случайная величина Х имеет данный закон распределения, то про нее говорят, что она «распределена по этому закону» или же подчиняется этому «закону распределения».
Наиболее общей формой закона распределения является функция распределения, представляющая собой вероятность того, что случайная величина Х примет значение меньшее чем заданное х:
F(x)=P{X<x}
Функция распределения F(x) для любой случайной величины обладает свойствами:
F(- 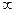 )=0 , F(+
)=0 , F(+ 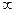 ) =1 , при возрастании х функция F(х) нет убывает. Наиболее простой вид имеют законы распределения у так называемых случайных величин. Случайная величина называется дискретной , если множество ее значений конечно или счетно.. В рассмотренных выше примерах случайная величина Х число попаданий при четырех выстрелах – дискретна. Ее возможные значения: 0,1,2,3,4.
) =1 , при возрастании х функция F(х) нет убывает. Наиболее простой вид имеют законы распределения у так называемых случайных величин. Случайная величина называется дискретной , если множество ее значений конечно или счетно.. В рассмотренных выше примерах случайная величина Х число попаданий при четырех выстрелах – дискретна. Ее возможные значения: 0,1,2,3,4.
Вторая величина Т –время наработки ЭВМ до первого отказа – недискретна, ее возможные значения непрерывно заполняют какой-то участок оси абсцисс, их множество несчетно.
Простейшей формой закона распределения дискретной случайной величины Х является ряд распределения- таблица, в верхней строке которой перечислены все значения случайной величины в порядке их возрастания, ав нижней соответствующие им вероятности:
| Х: | х1 | х2 | … | xi | ,,, |
| p1 | p2 | … | pi | … |
Где pi= P{X=xi); 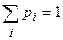
Функция распределения дискретной случайной величины Х есть разрывная ступенчатая функция скачки которой соответствуют возможным значениям х1, х2, …хn случайной величины Х и равны вероятностям р1,р2,…рnэтих значений; между скачками функция F(х) сохраняет постоянное значение. В точке разрыва функция F(х) равна тому значению с которым она подходит к точке разрыва слева. Функция F(х) «непрерывна слева».

Вероятность попадания случайной величины Х на участок от α до β (включая α) выражается через функцию распределения формулой
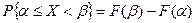 или в других обозначениях
или в других обозначениях
P{X 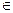 [α,β)} = F(β) – F(α)
[α,β)} = F(β) – F(α)
Где знаком [ обозначается то что точка α включается в состав отрезка от α до β, а знаком ) – что точка β в него не включается.
Математическим ожиданием случайной величины Х называется сумма произведений всех ее возможных значений на соответствующие вероятности:
M[X] = 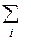 xipi
xipi
Математическое ожидание случайной величины может и не существовать если соответствующая сумма расходится. В случае, когда надо математическое ожидание случайной величины Х обозначить одной буквой пишут M[X] =mx.
Центрированной случайной величиной называется разность между случайной величиной Х и ее математическим ожиданием:
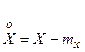
Дисперсией случайной величины Х называется математическое ожидание квадрата соответствующей центрированной случайной величины:
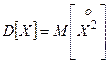
Для дискретной случайной величины Х дисперсия вычисляется по формуле
D[X] = 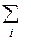 (xi-mi)2pi
(xi-mi)2pi
В случае когда надо дисперсию случайной величины Х обозначить одной буквой ее обозначают Dx.
Средним квадратичным отклонением случайной величины Х называется корень квадратный из ее дисперсии
σ[X] = σx = 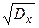
Подразумевается арифметическое или положительное значение корня.
Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой случайной величины:
αk[X] = M[Xk]
Для дискретной случайной величины Х начальный момент вычисляется по формуле
αk[X] = 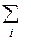 xikpi
xikpi
Центральным моментом k-го порядка случайной величины Х называется математическое ожидание соответствующей центрированной величины:
μk [X]=M[ 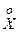 k]
k]
Для дискретной случайной величины Х центральный момент вычисляется по формуле
μk [X]= 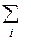 (хi-mx)k
(хi-mx)k
Математическое ожидание случайной величины Х есть ее первый начальный момент, а дисперсия – второй центральный.
М[Х]=α1[X] D[X]=μ2[X]
Формулы выражающие дисперсию через второй начальный момент
D[X]= α2[X] – mx2
D[X]==M[X2]-(M[X])2
Т.е. дисперсия равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания.
Индикатором события А называется дискретная случайная величина U имеющая два возможных значения 0 и 1, равная 0, если событие А не появилось и единице, если появилось.
Ряд распределения индикатора Uсобытия А имеет вид
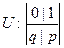 ,
,
Где р вероятность события в данном опыте; q=1-р
Математическое ожидание и дисперсия величины U равны соответственно
M[U]=p; D[U]=pq
Биноминальное распределение. Случайная величина Х называется распределенной по биноминальному закону, если ее возможные значения 0,1,2,…m,…,n а вероятность события {X=m} выражается формулой
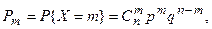 где
где
0<p<1 q=1-p; m=0,1,….n. Распределение зависит от двух параметров: p и n.
Из теоремы о повторении опытов следует, что число Х появлений события при n независимых опытах имеет биноминальное распределение с параметрами p и n.
M[X]=np D[X]=npq
Распределение Пуассона . Дискретная случайная величина Х называется распределенной по закону Пуассона, если ее возможные значения 0,1,2,…m,…, а вероятность события {X=m} выражается формулой
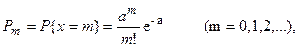
Где α>0. Распределение Пуассона зависит от одного параметра α. Для случайной величины распределенной по закону Пуассона,
M[X]=D[X]=α.
Пуассоновское распределение является предельным для биноминального при
p 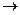 0, n
0, n 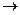
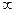 , если np=α=const. Этим распределением можно пользоваться приближенно если производится большое число независимых опытов в каждом из которых событие А происходит с малой вероятностью.
, если np=α=const. Этим распределением можно пользоваться приближенно если производится большое число независимых опытов в каждом из которых событие А происходит с малой вероятностью.
Геометрическое распределение. Говорят, что случайная величина Х имеет геометрическое распределение если ее возможные значения 0,1,2,…m,…, а вероятности ее значений
Рm=qm-1p 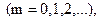
Где 0<p<1, q-1-p.
Вероятности Pm для ряда последовательных значений m образуют бесконечно убывающую геометрическую прогрессию со знаменателем q. На практике геометрическое распределение встречается когда производится ряд независимых попыток достигнуть какого-то результата А; при каждой «попытке» результат достигается с вероятностью р. Случайная величина Х – число «бесполезных» попыток (до первого опыта, в котором появится событие А). Ряд распределения случайной величины Х имеет вид
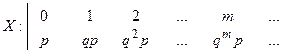
Математическое ожидание случайной величины Х имеющей геометрическое распределение равно
M[X]=q/p
А ее дисперсия
D[X]=q/p2
Контрольные вопросы
1. Что называют законом распределения случайной величины?
2. Что называют функцией распределения случайной величины?
3. Какую случайную величину называют дискретной?
4 Чему равно математическое ожидание дискретной случайной величины?
5. Что называют дисперсией случайной величины
6. Как вычисляют дисперсию дискретной случайной величины?
7. Что называют средним квадратическим отклонением?
8. Что называют индикатором события А и чему равен его ряд распределения?
9. Какая случайная величина называется распределенной по биноминальному закону?
10. Привести формулу Пуассона. Чему равны математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона?
Дата добавления: 2019-02-08; просмотров: 353;










