Детерминированное моделирование и преобразование факторных систем

Моделирование – это один из важнейших методов научного познания, с помощью которого создается модель (условный образ объекта исследовании. Сущность моделирования заключается в том, что взаимосвязь исследуемого показателя с факторными представляется в виде математического уравнения.

В факторном анализе различают модели детерминированные и стохастические. С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами). При моделировании детерминированных факторных систем необходимо выполнить ряд требований:

1. факторы, которые включаются в модель и сами модели должны реально существовать, а не быть придуманными абстрактными величинами или явлениями.

2. факторы, которые входят в систему, должны быть обязательными элементами формулы и находится в причинно – следственной связи с изучаемыми показателями. Построенная факторная система должна иметь познавательную ценность.

3. все показатели факторной модели должны быть количественно измеримыми, то есть должны иметь единицу измерения и необходимую информационную обеспеченность.

4. при построении модели в первую очередь учитываются количественные показатели, а затем качественные. Если имеется несколько количественных и несколько качественных показателей, то сначала исследуется величина факторов первого уровня соподчинения, а потом более низкого уровня. Например: объем валовой продукции зависит от четырех факторов:

- количества рабочих

- количества отработанных дней одним рабочим

- продолжительности рабочего дня

- среднечасовой выработки.

Этим обуславливается последовательность размещения факторов в модели и соответственно очередность их исследования, т.е.:

ВП=ЧР*Д*П*ЧВ

V этап. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов. В ней должна учитываться соразмерность изменений результативного и факторного показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.

В детерминированном анализе выделяют следующие типы факторных моделей:

- аддитивные модели – используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму факторных показателей:

У=х₁+х₂+…..+х_n=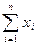

- мультипликативные – используются в тех случаях, когда результативный показатель представляет собой произведение нескольких факторов:

У=х₁*х₂*…..*х_n= 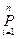х_i

- кратные – используются в случаях, когда результативный показатель получают делением одного фактора на величину другого:

У=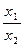

- смешанные (комбинированные) – представляют собой сочетание в различных комбинациях предыдущих моделей:

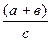У= 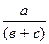; У= ; У=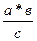

Для моделирования и преобразования факторных систем могут быть использованы следующие способы: расчленение, удлинение, формальное разложение, расширение, сокращение.

Расчленение – это разделение комплексных факторов на составные части. Например: объем реализации продукции равен объему производства продукции – остатки нереализованной продукции:

VРП=VВП-О_НП

Часть нереализованной продукции может находиться на складах организации (О_скл), а часть может быть отгружена покупателям, но еще не оплачена (О_отгр.). тогда приведенную модель можно записать следующим образом:

VРП=VВП-О_скл-О_отгр.

Для мультипликативных моделей:

ВП=ЧР*ГВ

ВП=ЧР*Д*ДВ

ВП=ЧР*Д*П*ЧВ

Удлинение - это удлинение числителя модели путем замены одного или нескольких факторов на сумму однородных показателей. Например, себестоимость единицы продукции можно представить в виде отношения двух факторов: суммы затрат к объему выпуска продукции:

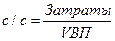
Если сумму затрат разложить на отдельные элементы, то получим аддитивную модель с новым набором факторов:

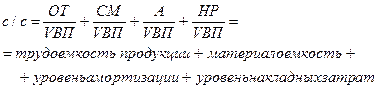
Формальное разложение – это удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей:

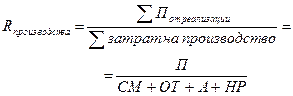
Расширение – это создание новой факторной модели путем умножения числителя и знаменателя дроби на один или несколько новых показателей:

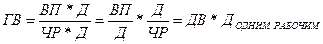
Сокращение – это создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель:

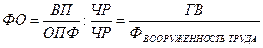
Выводы: процесс моделирования факторных систем очень сложный и ответственный момент в анализе хозяйственной деятельности. От того на сколько реально и точно созданные модели отражают связь между исследуемыми показателями зависят конечные результаты анализа.