Классификация систем радиоавтоматики
Cистемы радиоавтоматики можно классифицировать по параметру радиосигнала:
1) по фазе - системы фазовой автоподстройки;
2) по частоте - системы частотной автоподстройки;
3) по временному положению сигнала - системы временной автоподстройки;
4) по направлению прихода радиосигнала - системы угловой автоподстройки.
Cистемы радиоавтоматики можно классифицировать по характеру уравнения, описывающего процесс управления:
1) непрерывные или дискретные;
2) линейные или нелинейные;
3) cтационарные (с постоянными параметрами) или нестационарные (с переменными параметрами).
Cистемы радиоавтоматики можно классифицировать по поведению в условиях априорной неопределённости статистических характеристик задающего воздействия и помех:
1) минимаксные;
2) адаптивные;
3) инвариантные.
К фундаментальным принципам управления относятся принцип разомкнутого управления; принцип компенсации; принцип замкнутого управления.
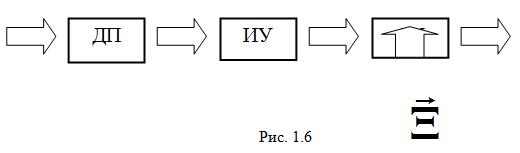
Принцип разомкнутого управления представлен на рис. 1.6.
ДП – датчик программы, ИУ – исполнительное устройство. В этом случае управление идёт по разомкнутому циклу.
Достоинство – простота. Недостаток – большая величина ошибки при воздействии помех на систему.
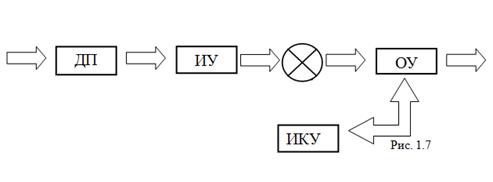
На рис. 1.7 показан принцип компенсации.
Определенное возмущение в ИКУ (измерительно-корректирующем устройстве) измеряется и вырабатывается корректирующее воздействие на ОУ, которое компенсирует отклонение, вызванное возмущением.
По сравнению с принципом разомкнутого управления точность САУ увеличивается. Недостаток этого принципа – система реагирует только на измеряемое возмущение. Этот принцип является принципом управления по возмущению.
Принцип замкнутого управления представлен на рис. 1.8.
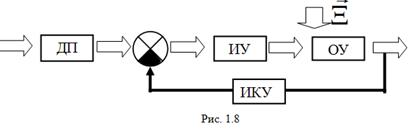
Принцип замкнутого управления отличается тем, что как бы не изменялось отклонение, всегда появляется сигнал, препятствующий этому отклонению.
На входе ИУ формируется вектор сигнала ошибки (рассогласования между требуемой и действительной величинами) 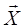 (
( 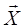 =
= 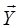 –
– 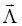 ).
).
ИКУ выполняет функцию коррекции и может отсутствовать.
 САР как динамическая система представляет собой систему регулирования, которая стремится сохранить ошибку в заданных пределах путем сравнения между собой заданной и действительной координат и использования получаемых при этом сигналов для управления источником энергии.
САР как динамическая система представляет собой систему регулирования, которая стремится сохранить ошибку в заданных пределах путем сравнения между собой заданной и действительной координат и использования получаемых при этом сигналов для управления источником энергии.
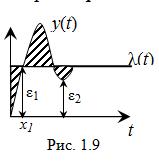
Отклонение – разность между действительным значением выходной переменной величины в текущий и в начальный моменты времени (рис. 1.9). Заштрихованная область на рис. 1.9 – ошибка регулирования.
Если с течением времени ошибка в установившемся режиме на выходе системы больше нуля, то говорят, что данная система – статическая.
У астатической системы установившееся значение x(t) стремится к нулю. Система может рассматриваться как статическая или астатическая и по отношению к возмущению, и по управляющему воздействию. Возможны системы астатические по управляющему воздействию и статические по возмущению. При проектировании желательно стремиться, чтобы системы были астатическими.
Математическое описание линейных стационарных систем. Преобразования Лапласа, Фурье .Связь операторного коэффициента передачи передаточной функции, переходной и импульсной характеристик.
Процессы в системах радиоавтоматики описываются линейными дифференциальными уравнениями вида:
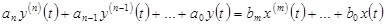 , (2.1)
, (2.1)
где левая часть уравнения описывает преобразование выходного сигнала объекта управления, а правая часть описывает пребразование входного воздействия.
Решение дифференциального уравнения (2.1) связано с вычислительными трудностями, а во многих случаях, например в следящих системах, не может быть осуществлено, т.к. не известно управляющее воздействие.
Для исследования систем радиоавтоматики используются следующие основные характеристики, которые будут рассмотрены ниже: передаточная функция, переходная и импульсная переходная функции, комплексный коэффициент передачи или частотная характеристика.
2.1. Передаточная функция
Преобразованием Лапласа называется функциональное преобразование вида
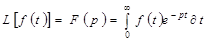 .
.
Применим к (2.1) преобразование Лапласа, получим:
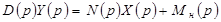 ,
,
где
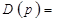
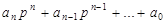 ;
; 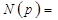
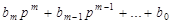 ;
;
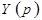 - преобразование Лапласа для выходного сигнала системы;
- преобразование Лапласа для выходного сигнала системы;
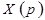 - преобразование Лапласа для входного сигнала;
- преобразование Лапласа для входного сигнала;
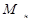 - многочлен, отображающий начальные условия.
- многочлен, отображающий начальные условия.
Введём обозначения:
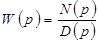 ;
; 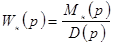 .
.
Тогда
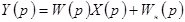 .
.
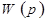 характеризует динамические свойства системы радиоавтоматики, она не зависит от управляющего воздействия и полностью определяется параметрами системы
характеризует динамические свойства системы радиоавтоматики, она не зависит от управляющего воздействия и полностью определяется параметрами системы  и
и 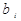 . Эту функцию называют передаточной. При нулевых начальных условиях
. Эту функцию называют передаточной. При нулевых начальных условиях 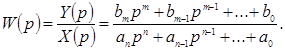
Пример 2.1. Найти передаточную функцию системы радиоавтоматики, если входное воздействие может быть описано функцией 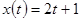 , а выходной сигнал может быть описан функцией
, а выходной сигнал может быть описан функцией 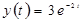 .
.
По определению передаточной функции 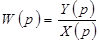 . По таблице преобразований Лапласа (см. Приложение):
. По таблице преобразований Лапласа (см. Приложение): 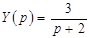 ,
, 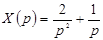 . Тогда
. Тогда
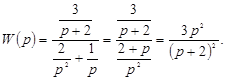
2.2. Переходная функция и импульсная переходная функции
Переходный процесс физически означает переходный процесс в системе радиоавтоматики, вызванный входным сигналом в виде единичной функции.
Пусть 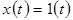 - единичный сигнал, действующий на систему радиоавтоматики, т.е. сигнал, описываемый функцией следующего вида:
- единичный сигнал, действующий на систему радиоавтоматики, т.е. сигнал, описываемый функцией следующего вида:
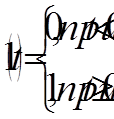
В этом случае:
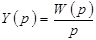 - преобразование Лапласа для выходного сигнала системы (cм. Приложение),
- преобразование Лапласа для выходного сигнала системы (cм. Приложение),
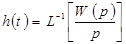 - переходная функция.
- переходная функция.
Переходный процесс, возникающий в системе радиоавтоматики при действии единичного импульса, называют импульсной переходной функцией.
Пусть 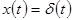 - cигнал вида
- cигнал вида 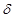 -функции, удовлетворяющий условиям:
-функции, удовлетворяющий условиям:
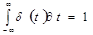 ;
; 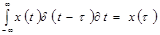 .
.
Тогда
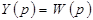 - преобразование Лапласа для выходного сигнала системы (см.Приложение),
- преобразование Лапласа для выходного сигнала системы (см.Приложение),
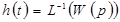 - импульсная переходная функция.
- импульсная переходная функция.
Пример 2.2. Найти переходную и импульсную переходную функцию системы, передаточная функция которой 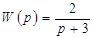 .
.
По определению переходной функции: 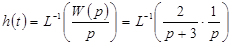 .
.
Разложим выражение 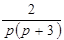 в сумму элементарных дробей:
в сумму элементарных дробей:
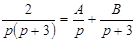 , где
, где 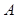 и
и 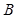 - некоторые числа.
- некоторые числа.
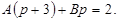
Из этого выражения cледует:
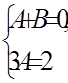
Тогда 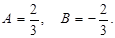
Таким образом, 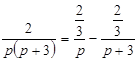 .
.
По таблице преобразований Лапласа имеем:
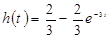 .
.
По определению импульсной переходной функции:
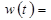
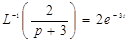 .
.
Дата добавления: 2020-10-25; просмотров: 825;











