Типовые радиотехнические звенья
Устройства систем РА, имеющие различное конструктивное исполнение и принципы работы, могут описываться одинаковыми дифференциальными уравнениями. Устройства систем РА, классифицируемые по виду передаточных функций, называют типовыми радиотехническими звеньями. При моделировании типовых радиотехнических звеньев принимаются следующие допущения:
§ система разбивается на возможно простые звенья;
§ типовое радиотехническое звено имеет лишь одну входную и одну выходную величину и описывается одной передаточной функцией;
§ звенья обладают направленностью действия с входа на выход;
§ состояние звена не влияет на состояние предшествующего звена, работающего на его вход.
Передаточная функция типового радиотехнического звена в общем виде представляется как произведение сомножителей следующего вида [3]:
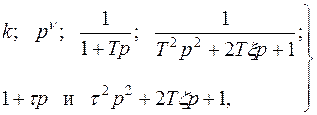 (4.16)
(4.16)
где k, n, T, x, t, z – постоянные, причем k > 0, где n может быть положительным и отрицательным целым числом, T > 0, 0 £ x < 1, t > 0, 0 £ z < 1.
В соответствии с видом сомножителей (4.16) в табл. 4.1 приведены типовые радиотехнические звенья. В ней даны дифференциальные уравнения и передаточные функции этих звеньев, и показано их деление по основным свойствам на три группы: позиционные, интегрирующие и дифференцирующие.
Таблица 4.1 - Типовые звенья радиоавтоматики
| Тип звена | Дифференциальное уравнение | Передаточная функция W=W(p) | ||
| Позиционные звенья | Идеальное усилительное (безынерционное) | 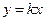
| 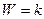
| |
| Апериодическое (инерционное) | 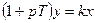
| 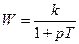
| ||
| Апериодическое (инерционное) второго порядка | 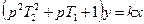 , где , где 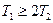
| 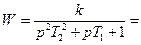 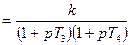 , где , где 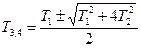
| ||
| Колебательное | 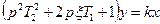 , где , где 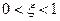
| 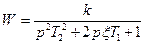
| ||
| Консервативное | 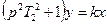
| 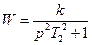
| ||
| Интегрирующее | Интегрирующее идеальное | 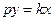
| 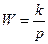
| |
| Интегрирующее инерционное | 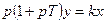
| 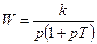
| ||
| Изодромное | 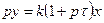
| 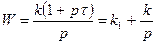 , где k1=kt , где k1=kt
| ||
| 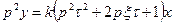 , где , где 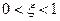
| 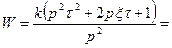 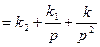 ,
где k1 = 2kxt; k2 = kt2; ,
где k1 = 2kxt; k2 = kt2;
| ||
| Дифференцирующее | Дифференцирующее идеальное | 
| 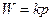
| |
| Дифференцирующее инерционное | 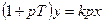
| 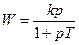
| ||
| Форсирующее идеальное | 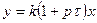
| 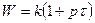
| ||
| Форсирующее идеальное второго порядка | 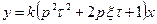 , где , где 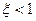
| 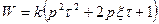
| ||
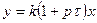
| 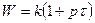
|
Примечание: обозначения, принятые в таблице 4.1: k – коэффициент усиления; T, t – постоянные времени; x – коэффициент демпфирования (относительный коэффициент затухания); p – оператор Лапласа и дифференцирования.
Позиционные звенья, кроме консервативного, характеризуются тем, что в каждом из них при подаче на вход постоянной величины с течением времени устанавливается постоянное значение выходной величины. Отношение установившихся значений выходной и входной величин называют передаточным коэффициентом k звена.
В безынерционном (идеальном) звене при скачкообразном изменении входной величины мгновенно без какого-либо запаздывания изменяется и выходная величина – переходного процесса нет. В апериодическом звене выходная величина нарастает монотонно. Продолжительность переходного процесса зависит от второго параметра звена, называемого постоянной времени T. Чем больше постоянная времени, тем медленнее протекает переходной процесс.
В апериодическом звене второго порядка переходной процесс также монотонный, но его продолжительность зависит от двух постоянных времени T1, T2.
Выходная величина колебательного звена в переходном процессе совершает колебания около того значения, которое должно установиться. Затухание колебаний зависит от значения третьего параметра звена, называемого коэффициентом демпфирования x, который лежит в пределах от нуля до единицы. Чем больше x, тем меньше отклонения и тем быстрее заканчивается переходной процесс.
Консервативное звено есть вырожденный случай колебательного звена (x= 0). Возникшие в нем колебания не затухают. Передаточный коэффициент k указывает отношение амплитуды гармонических колебаний выходной величины к постоянной входной величине.
Интегрирующие звенья характеризуются тем, что при постоянном входном воздействии выходная величина неограниченно растет. У идеального интегрирующего звена передаточный коэффициент k определяет скорость этого роста. У реального интегрирующего звена такой режим устанавливается позднее и зависит от постоянной времени T.
В изодромных звеньях имеет место некоторый начальный скачок выходной величины и затем ее неограниченное нарастание. Передаточный коэффициент k изодромного звена первого порядка определяет скорость последующего нарастания выходной величины, а изодромного звена второго порядка – постоянное ускорение, с которым нарастает выходная величина.
Дифференцирующие звенья реагируют лишь на изменения входной величины. Например, если входная величина идеального дифференцирующего звена нарастает с постоянной скоростью, то выходная величина удерживается на постоянном уровне, пропорциональном этой скорости.
В природе идеальных дифференцирующих звеньев нет – они всегда имеют некоторую (хотя бы и очень малую) инерционность. При линейном нарастании входной величины реального дифференцирующего звена постоянное значение его выходной величины устанавливается не сразу, а тем позже, чем больше постоянная времени T.
Форсирующие звенья сочетают в себе свойства позиционного и дифференцирующего звеньев.
В инженерной практике при анализе и исследовании систем РА используют семь видов типовых звеньев: безынерционные, инерционные, интегрирующие, колебательные, идеальные дифференцирующие, реальные дифференцирующие первого порядка и звенья запаздывания. Рассмотрим их основные передаточные свойства.
Безынерционное (пропорциональное) звено. К числу таких звеньев относятся устройства с передаточной функцией 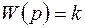 , где k – коэффициент передачи звена. Амплитудная и фазочастотная характеристики звена:
, где k – коэффициент передачи звена. Амплитудная и фазочастотная характеристики звена: 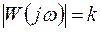 ,
, 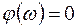 ; переходная функция
; переходная функция 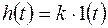 . ЛАЧХ и фазовая частотная характеристика звена не зависит от частоты (рис. 4.10).
. ЛАЧХ и фазовая частотная характеристика звена не зависит от частоты (рис. 4.10).
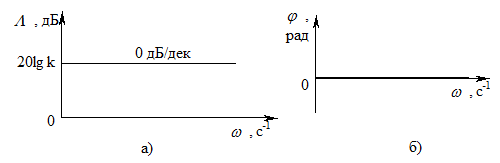
Рис. 4.10 - Логарифмические амплитудная (а) и фазовая (б) частотные
характеристики безынерционного звена
Примерами таких звеньев являются потенциометр, полупроводниковый усилитель, операционный усилитель, зубчатая передача и т.п.
Инерционное (апериодическое) звено. К подобным звеньям относятся устройства с передаточной функцией
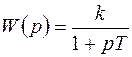 . (4.17)
. (4.17)
Пример инерционного звена – RC-цепочка (рис. 4.11, а). Частотная характеристика инерционного звена имеет вид
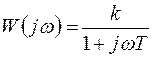 .
.
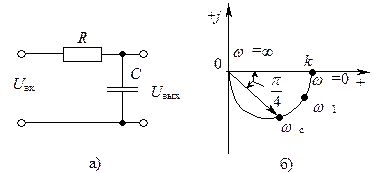
Рис. 4.11 - Схема (а) и годограф (б) RC-цепи инерционного звена
Вещественная и мнимая частотные характеристики:
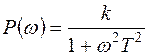 ;
; 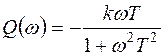 ;
;
амплитудная и фазовая характеристики:
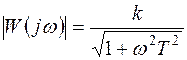 ;
; 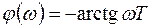 . (4.18)
. (4.18)
Годограф инерционного звена (рис. 4.11, б) имеет сопрягающую частоту wс =1/T .
Переходная функция звена находится по формуле (3.10) и имеет вид
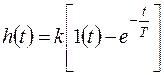 .
.
Импульсная переходная функция находится по формуле (3.16).
Логарифмическая частотная характеристика инерционного звена в соответствии с выражением (3.29) и (4.18) имеет вид
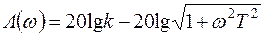 . (4.19)
. (4.19)
Предварительно построим приближенную характеристику в диапазоне частот от 0 до сопрягающей частоты wс=1/Т, пренебрегая в (4.19) слагаемым, зависящим от частоты (оно меньше единицы), получим 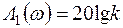 . Этому выражению соответствует прямая линия, параллельная оси частот (рис. 4.12, а). На частотах больших сопрягающей частоты wс пренебрежем единицей. Тогда (4.19) будет иметь вид
. Этому выражению соответствует прямая линия, параллельная оси частот (рис. 4.12, а). На частотах больших сопрягающей частоты wс пренебрежем единицей. Тогда (4.19) будет иметь вид 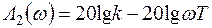 . Так как частота по оси абсцисс откладывается в логарифмическом масштабе, то этому выражению соответствует прямая линия с наклоном –20 дБ/дек.
. Так как частота по оси абсцисс откладывается в логарифмическом масштабе, то этому выражению соответствует прямая линия с наклоном –20 дБ/дек.
Характеристику, составленную из прямых отрезков L1 и L2, называют асимптотической. Наибольшее отклонение асимптотической характеристики от точной получается на сопрягающей частоте; оно равно – 3 дБ. На частотах, отличающихся от сопрягающей на одну октаву, отклонение составляет –1 дБ.
Логарифмическую фазочастотную характеристику (рис. 4.12, б) строят в соответствии с выражением (4.18).
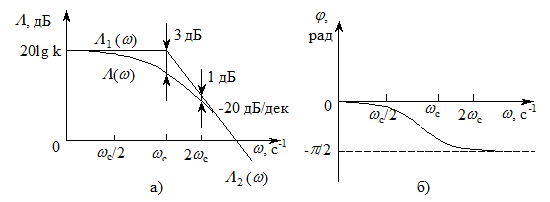
Рис. 4.12 - Логарифмическая амплитудночастотная (а) и фазочастотная (б) характеристики инерционного звена
Интегрирующее звено. К числу таких звеньев относятся устройства с передаточной функцией
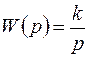 . (4.20)
. (4.20)
Годограф интегрирующего звена приведен на рис. 4.13.
Примеры интегрирующего звена: электрический двигатель с передаточной функцией (4.15), если в ней пренебречь электромеханической постоянной времени; усилитель постоянного тока с большим коэффициентом усиления, в цепь обратной связи которого включен конденсатор.
Вещественная, мнимая и частотные характеристики интегрирующего звена имеют вид:
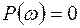 ;
; 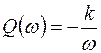 ,
,
амплитудная и фазовая характеристики:
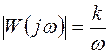 ;
; 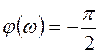 . (4. 21)
. (4. 21)
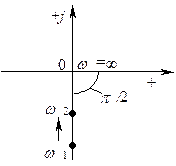
Рис. 4.13 - Годограф частотной характеристики
интегрирующего звена
Логарифмическая АЧХ звена с учетом (3.29) и (4.21) определяется выражением 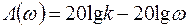 .
.
Этому уравнению соответствует прямая линия с наклоном –20 дБ/дек (рис. 4.14, а). Логарифмическая ФЧХ (4.21) не зависит от частоты и равна –p/2 (рис. 4.14, б).
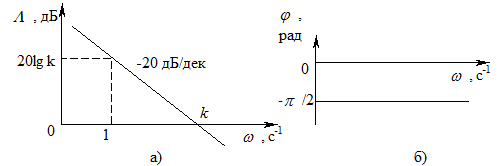
Рис. 4.14 - Логарифмическая (а) и фазовая (б) частотная
характеристика интегрирующего звена
Колебательное звено. Передаточная функция звена имеет вид
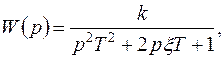 (4.22)
(4.22)
где x – относительный коэффициент затухания.
Примером колебательного звена является контур, состоящий из индуктивной катушки, резистора и конденсатора (рис. 4.15, а).
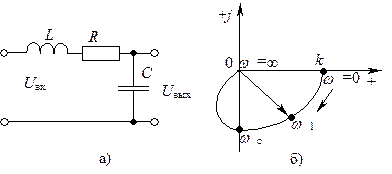
Рис. 4.15 - Схема (а) и годограф частотной характеристики (б)
колебательного звена
Амплитудная и фазовая частотные характеристики колебательного звена соответственно имеют вид:
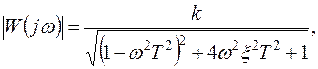
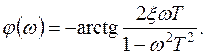 (4.23)
(4.23)
Переходная функция звена в соответствии с (3.10)
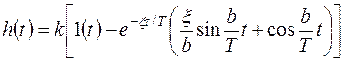 ,
,
где 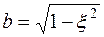 .
.
Если x > 1, то полюсы передаточной функции (4.22) – отрицательные действительные числа, поэтому передаточную функцию звена можно представить в виде
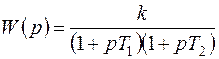 ,
,
где T1 = 1/l1; T2 = 1/l2.
С учетом (3.29) ЛАЧХ колебательного звена будет определяться выражением
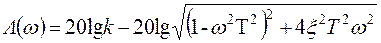 .
.
Приближенная характеристика звена состоит из двух участков. На участке до сопряженной частоты 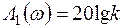 с наклоном 0 дБ/дек, в диапазоне частот больше сопряженной
с наклоном 0 дБ/дек, в диапазоне частот больше сопряженной 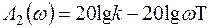 с наклоном –40 дБ/дек (рис. 4.16).
с наклоном –40 дБ/дек (рис. 4.16).
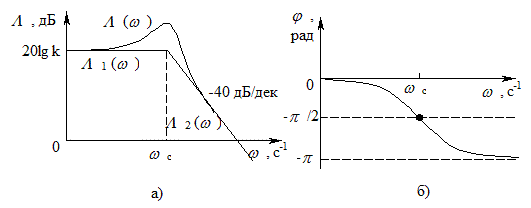
Рис. 4.16 - Логарифмическая (а) и фазовая (б) частотная
характеристика инерционного звена
Максимальное отклонение точной характеристики от приближенной получается на сопряженной частоте и равно – 20 lgx. Уточнение приближенной характеристики производится расчетным путем. Логарифмическую ФЧХ строят в соответствии с выражением (4.23).
Идеальное дифференцирующее звено. Передаточная функция звена 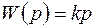 не удовлетворяет условию физической реализуемости, поэтому звено называют идеальным. Годограф звена изображен на рис. 4.17. Частотные характеристики звена имеют вид
не удовлетворяет условию физической реализуемости, поэтому звено называют идеальным. Годограф звена изображен на рис. 4.17. Частотные характеристики звена имеют вид
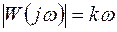 ;
; 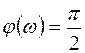 . (4.24)
. (4.24)
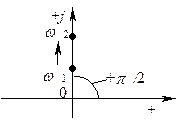
Рис. 4.17 - Годограф частотной характеристики идеального
дифференцирующего звена
Переходная функция звена имеет вид 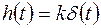 , где
, где 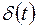 – дельта-функция.
– дельта-функция.
Логарифмическая АЧХ звена в соответствии с (3.29) и (4.24) определяется как
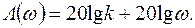
Этому уравнению соответствует прямая линия с наклоном + 20 дБ/дек (рис. 4.18, а). Логарифмическая ФЧХ (4.21) не зависит от частоты и равна + p/2 (рис. 4.18, б).
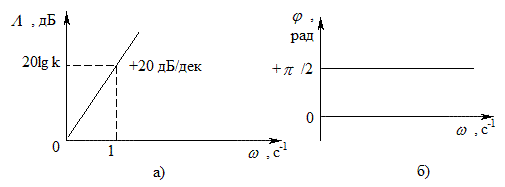
Рис. 4.18 - Логарифмическая (а) и фазовая (б) частотная характеристика идеального дифференцирующего звена
Дифференцирующее звено первого порядка. Передаточная функция звена дифференцирующего (форсирующего) звена имеет вид 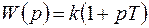 (рис. 4.19), а частотная и фазовая характеристики соответственно:
(рис. 4.19), а частотная и фазовая характеристики соответственно:
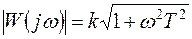 ;
; 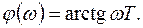 (4.25)
(4.25)
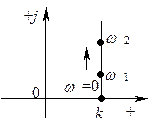
Рис. 4.19 - Годограф частотной характеристики дифференцирующего
звена первого порядка
Переходная функция звена имеет вид 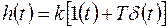 , где
, где 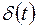 - дельта функция.
- дельта функция.
Логарифмическая частотная характеристика форсирующего звена в соответствии с выражением (3.29) и (4.25) имеет вид
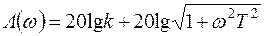 . (4.26)
. (4.26)
Приближенная характеристика форсирующего звена в диапазоне частот от 0 до сопряженной частоты wс=1/Т имеет вид 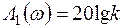 . Этому выражению соответствует прямая линия, параллельная оси частот (рис. 4.20, а). На частотах больших сопряженной частоты wс, пренебрегая единицей, характеристика (4.26) будет иметь вид
. Этому выражению соответствует прямая линия, параллельная оси частот (рис. 4.20, а). На частотах больших сопряженной частоты wс, пренебрегая единицей, характеристика (4.26) будет иметь вид 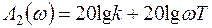 . Так как частота по оси абсцисс откладывается в логарифмическом масштабе, то этому выражению соответствует прямая линия с наклоном –20 дБ/дек.
. Так как частота по оси абсцисс откладывается в логарифмическом масштабе, то этому выражению соответствует прямая линия с наклоном –20 дБ/дек.
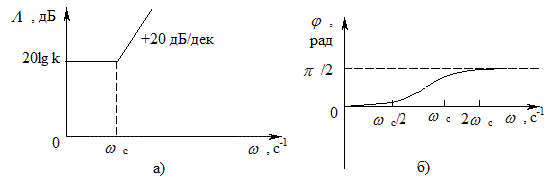
Рис. 4.20 - Логарифмическая (а) и фазовая (б) частотная характеристика дифференцирующего звена первого порядка
Звено запаздывания. Это звено используется для моделирования сдвига входного сигнала во времени, не искажая его ЛАЧХ и фазочастотной характеристик. Передаточная функция звена имеет вид 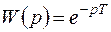 , где T – время запаздывания. Частотные характеристики имеют вид
, где T – время запаздывания. Частотные характеристики имеют вид
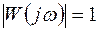 ;
; 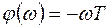 .
.
Годограф звена запаздывания имеет вид окружности с единичным радиусом (рис. 4.21).
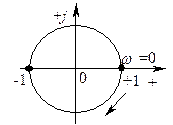
Рис. 4.21 - Годограф частотной характеристики
звена запаздывания
Переходная функция, ЛАЧХ и фазочастотная характеристика звена запаздывания, как отмечалось ранее, не искажают характеристики системы РА в целом.
Дата добавления: 2020-10-25; просмотров: 1094;











