Неавтономные системы, параметрический генератор

В пункте 1.1. вводилось определение неавтономных систем, и отмечались способы воздействия на неавтономную систему. Рассмотрим на конкретных примерах силовое и параметрическое воздействия. Начнём с силового воздействия: для этого вернёмся к генератору на туннельном диоде с дополнительным источником напряжения (рис. 16), который и играет роль внешнего воздействия.

Уравнение, описывающее колебательные процессы в этом генераторе, от (1.13) будет отличаться тем, что добавится внешнее воздействие:

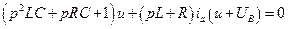.	(1.24)
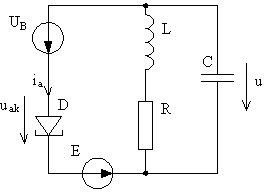Рис. 16. Генератор на туннельном диоде.	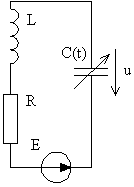Рис. 17. Колебательный контур.

Перейдём к параметрическому воздействию и рассмотрим контур, изображённый на рис. 17. При определённой частоте внешнего воздействия (при резонансе) возможна потеря устойчивости и возникновение колебаний с частотой кратной частоте внешнего воздействия. Опишем эту систему. В качестве обобщённых координат возьмём заряд. Для простоты также пусть Е = 0, тогда, так как u = q/C(t), уравнение колебательного контура запишется в виде:

.

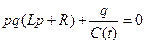В частном случае (если в качестве переменной ёмкости - варикап), т. е. справедлива следующая зависимость

,

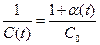символическое уравнение системы принимает вид:

.

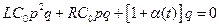(1.25)

Если a(t) меняется по гармоническому закону, то получится уравнение Матье, а при произвольном изменении - уравнение Хилла.