Уравнение Лагранжа для колебательных систем Вопрос 3
Уравнение движения Лагранжа удобно тем, что уравнение движения записывается в ковариантной форме, т. е. структура уравнения не меняется при переходе к другим координатам.
Любая механическая система описывается уравнением Ньютона:
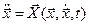 , ,
| (1.26) |
и это самая общая форма записи (форма Коши). Известно, что, если заданы начальные условия
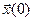 и
и 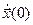 ,
,
то решение существует и единственно.
В общем случае на уравнение накладываются связи, уменьшая количество независимых координат:
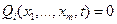 , где , где 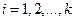 . .
| (1.27) |
Если у нас есть k связей, то только n = m - k координат являются обобщёнными. Выбираем обобщённые координаты q1, …, qn так, чтобы их связь с первичными была точечной:
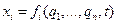 , где , где 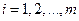 . .
| (1.28) |
Допустим, что силы, действующие на систему, являются потенциальными, т. е. существует функция 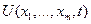 такая, что для каждой силы выполняется равенство
такая, что для каждой силы выполняется равенство
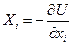 , где
, где 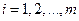 .
.
В этом случае для описания движения в потенциальном поле можно воспользоваться формализмом Лагранжа:
1. Выбираем обобщённые координаты q1, …, qn.
2. С помощью уравнения преобразования координат (1.28) записываем выражение для энергии через эти координаты:
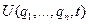 .
.
3. С учётом преобразования обобщённых скоростей
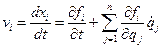
| (1.29) |
строим выражение для кинетической энергии системы 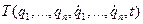 .
.
4. Составляем лагранжиан системы 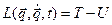 .
.
5. Записываем уравнение движения системы в виде:
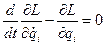 , где , где 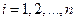 . .
| (1.30) |
Из (1.30) можно непосредственно найти первый интеграл движения:
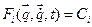 . .
| (1.31) |
Коэффициенты Ci можно найти из начальных условий.
Лагранжев формализм работает только в потенциальном поле, но, если в системе действуют диссипативные силы Qi (трение, потери), то в общем случае уравнение Лагранжа выглядит так:
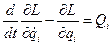 , где , где 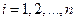 . .
| (1.32) |
Простейший случай, когда диссипативные силы являются линейной функцией обобщённых скоростей:
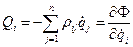 .
.
Для линейной функции можно построить функцию Рэлея, тогда диссипативные силы - это частные производные по обобщённым координатам функции Рэлея:
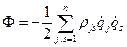
| (1.33) |
В этом случае уравнение Лагранжа примет ещё более простой вид:
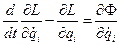 , где , где 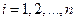 , ,
| (1.34) |
т. е. для полного описания системы с диссипацией нужно задать две функции: L и F.
Если точечное преобразование (1.28) не содержит в явном виде времени, то
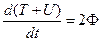 . .
| (1.35) |
Таким образом, энергия системы убывает со скоростью, равной удвоенной функции Рэлея.
Дата добавления: 2019-02-08; просмотров: 949;











