Поверхности вращения
Пусть произвольная линия AGEB вращается вокруг оси i. Тогда она образует поверхность вращения (рис. 4.1).
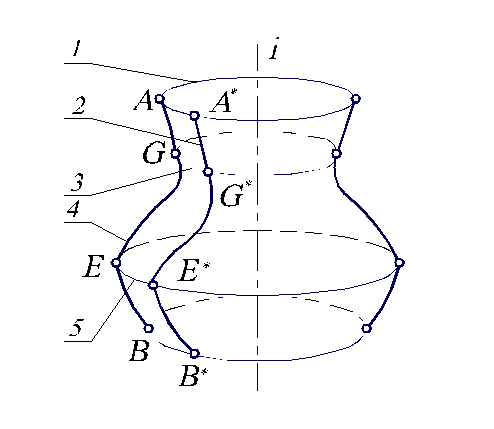
Рис. 4.1. Образование поверхности вращения.
Линия пересечения поверхности вращения плоскостью, проходящей через ось i, называется меридианом (например A*G*E*B*). Меридиан, лежащий в плоскости, параллельной П2, называется главным. Линия пересечения поверхности вращения плоскостью, перпендикулярной оси i, называется параллелью. Таковыми являются направляющие, проходящие через точки АА*, ВВ*, ЕЕ*, GG*. Параллель, проходящая через наиболее удаленную от оси точку Е образующей, называется экватором, а через самую близкую точку G – горлом. Очевидно, что все параллели представляют собой окружности.
Одной из самых простых поверхностей вращения является цилиндр. Цилиндрическая поверхность образуется при вращении прямой (образующей) АВ вокруг оси (рис. 4.2, а). Образование цилиндрической поверхности подобно получению призматической с той лишь разницей, что у гранной поверхности направляющей является ломаная линия.
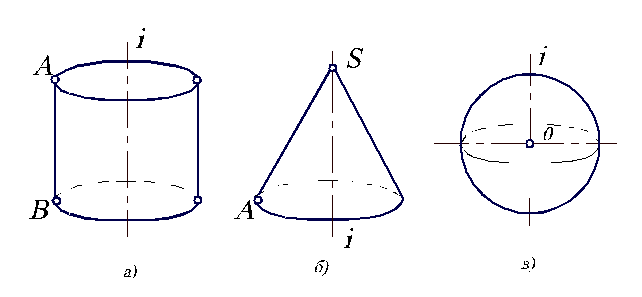
Рис. 4.2. Образование поверхности цилиндра, конуса, сферы.
В случае образования конической поверхности прямая AS, вращающаяся вокруг оси, закреплена в некоторой точке S на оси (рис. 4.2, б). Такая поверхность подобна пирамидальной, у которой образующей является тоже прямая, но перемещающаяся по ломаной линии. Для того, чтобы получить цилиндр или конус, надо соответствующую поверхность ограничить плоскостями основания.
Если в качестве образующей выбираем окружность, то при ее вращении вокруг оси получаем:
— сферу, когда ось вращения проходит через центр О окружности (рис. 4.2, в);
— тор, в противном случае (рис. 4.3).
Если ось вращения проходит через образующую–окружность, тор получается закрытым (рис. 4.3, а), в противном случае-открытым (рис. 4.3, б). Примером открытого тора может служить бублик, закрытого – яблоко либо лимон.
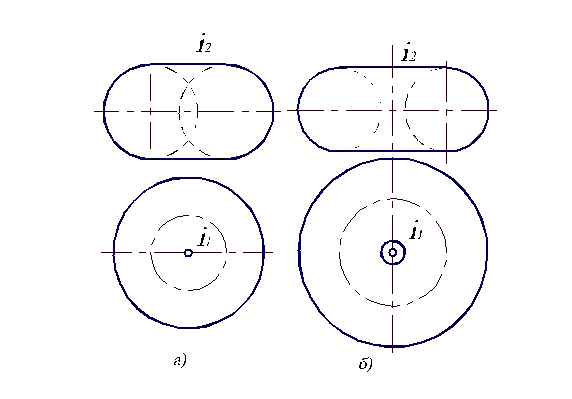
Рис. 4.3. Образование поверхности тора.
Дата добавления: 2016-07-27; просмотров: 1953;











