Определение натуральной величины фигуры сечения

Нередко практический интерес представляет задача определения натуральной величины фигуры сечения.

Определим натуральную величину сечения (четырехугольника), полученного на рис. 3.11. Так как четырехугольник 1234 занимает общее положение в пространстве, то его натуральную величину можно определить двумя переменами плоскостей проекций, сначала построив плоскость, перпендикулярную четырехугольнику 1234, а затем – параллельную ему. Чтобы не загромождать чертеж (рис. 3.11), вынесем построения на отдельный рисунок 3.12. Для построения плоскости, перпендикулярной плоскости четырехугольника 1234, необходимо начертить одну из главных линий, например, горизонталь. Ее фронтальная проекция h₂ должна быть параллельна оси П₁/П₂. По точкам пересечения 2 и 4 с четырехугольником 1234 находим и горизонтальную проекцию h₁ горизонтали.

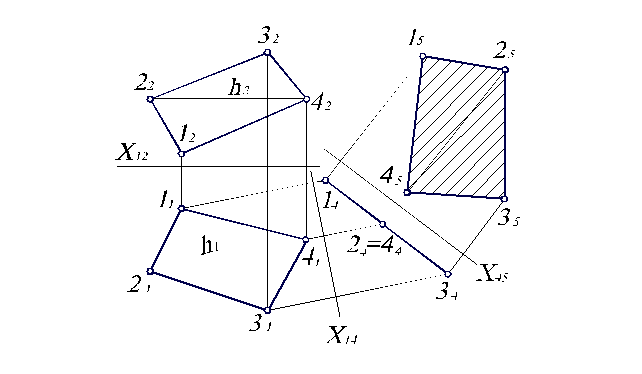
Новая ось П₄/П₁, разделяющая П₁ и новую плоскость П₄, должна быть перпендикулярна h₁. Затем получаем проекцию 1₄2₄3₄4₄ в виде прямой. И наконец, вычертив вторую новую ось П₅/П₄, параллельно 1₄3₄, построим проекцию 1₅2₅3₅4₅ четырехугольника в плоскости П₅. Это и есть натуральная величина четырехугольника 1234. Сечение заштрихуем под углом 45° к горизонтальной прямой.

Чаще приходится решать более простую задачу – определение натуральной величины сечения многогранника плоскостью частного положения. В этом случае достаточно сделать всего одну замену плоскостей проекций. Рассмотрим на примере сечения пирамиды горизонтально–проецирующей плоскостью S (рис 3.13). Пусть задана горизонтальная проекция S₁. Необходимо найти линию пересечения плоскости S с пирамидой и определить натуральную величину сечения. Таким образом, задача разбивается на две части: сначала надо построить сечение в плоскостях П₁и П₂, а затем определить его натуральную величину.

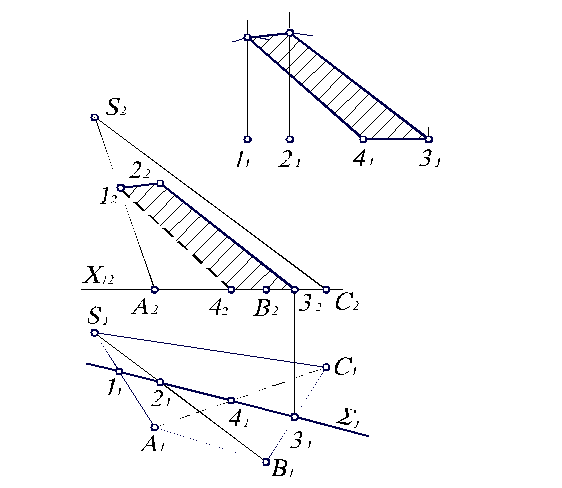
Рис. 3.13. Построение линии пересечения и определение натуральной величины сечения пирамиды плоскостью.

Чтобы решить первую часть задачи нужно найти все точки пересечения плоскости S с ребрами пирамиды и соединить их отрезками прямой. Горизонтальная проекция S₁ пересекает ребра пирамиды в точках 1₁, 2₁, 3₁, 4₁ (рис. 3.13, а). По линиям связи находим их фронтальные проекции 1₂, 2₂, 3₂, 4₂ на фронтальных проекциях соответствующих ребер. Соединяя найденные точки, получаем линию пересечения 1₂2₂3₂4₂ заданной плоскости с пирамидой. Отрезок 1₂4₂ этой линии будет невидимым, так как он лежит на невидимой грани A₂S₂C₂. Плоская фигура, ограниченная полученной линией (на рис. 5.9, а заштрихована), и является сечением пирамиды плоскостью. В нашем примере это четырехугольник 1234.

Для определения натуральной величины четырехугольника 1234 способом замены плоскостей проекций не обязательно строить новую ось параллельно S₁ (или 1₁2₁4₁3₁), ввиду ограниченности площади чертежа. Достаточно соблюдать основные принципы построения. Начертим новую ось на свободном поле чертежа. Перенесем на нее точки 1₁,2₁,4₁,3₁, не меняя расстояния между ними. Проведем через них перпендикуляры к оси. Затем отложим на построенных перпендикулярах отрезки, равные расстояниям от оси П₂/П₁, которую считаем расположенной на основании А₂В₂С₂ пирамиды, до соответствующих проекций 1₂, 2₂, 4₂, 3₂. Соединив указанные точки, получим натуральную величину сечения пирамиды заданной плоскостью S (рис. 3.13, б).

Как видим, сечение в натуральную величину отличается от 1₂2₂3₂4₂ лишь тем, что оно вытянуто вдоль S₁.