Цифровые системы радиоавтоматики

10.1.Общая характеристика цифровых систем

В цифровых системах радиоавтоматики обработка сигналов производится цифровыми методами, а их реализация – на элементах цифровой схемотехники.

Рассмотрим достоинства и недостатки цифровых систем.

К достоинствам можно отнести высокую технологичность настройки, высокую надежность, возможность реализации оптимальных алгоритмов обработки, достаточно низкую стоимость, гарантированную точность, стабильность параметров.

Недостатки цифровых систем связаны с дискретизацией по времени и квантованию по уровню, что приводит к возникновению шумов квантования.

Функциональная схема цифровой системы представлена на рис. 10.1

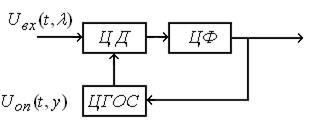
Рис. 10.1. Функциональная схема цифровой следящей системы:

ЦД – цифровой дискриминатор; ЦФ – цифровой фильтр; ЦГОС – цифровой генератор опорного сигнала.

Цифровые системы радиоавтоматики классифицируют по тем же признакам, что и аналоговые системы. Дополнительным признаком классификации является место аналого-цифрового преобразования. Различают системы, в которых АЦП производится вне контура регулирования и внутри его. В первом случае на дискриминатор поступают цифровые сигналы, во втором – аналоговые, при этом в дискриминаторе производится аналого-цифровое преобразование и на выходе дискриминатора формируется цифровой сигнал.

10.2. Аналого-цифровая следящая система

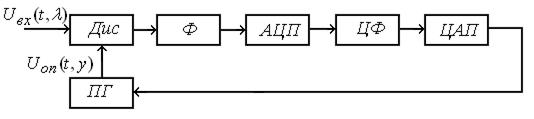
Рис. 10.2. Функциональная схема аналого-цифровой следящей системы

Функциональная схема аналого-цифровой следящей системы приведена на рис. 10.2.

Фильтр Ф ограничивает ширину спектра сигнала на выходе дискриминатора, что необходимо для дальнейшего аналого-цифрового преобразования. Основная фильтрация производится цифровым фильтром ЦФ, который позволяет обеспечить идеальное интегрирование, реализовать оптимальные алгоритмы фильтрации. Рассмотрим функции АЦП.

АЦП предназначен для преобразования напряжения, пропорционального сигналу ошибки, в цифровой код. АЦП выполняет две операции:

дискретизацию по времени, при этом U(t) – непрерывная функция преобразуется в дискретную функцию U(kT);квантование по уровню:

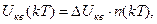
где ΔU_кв – дискрет квантования по уровню; n – число, соответствующее данному уровню.

Операция квантования по уровню и замена квантованного напряжения кодом, может быть представлена как нелинейная операция (рис. 10.3)

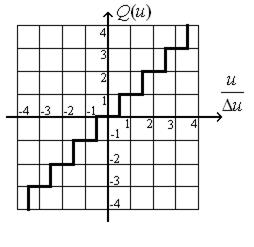
Рис.10.3.

Цифровой фильтр ЦФ преобразует последовательность чисел, поступающую на вход 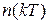, в сглаженную последовательность 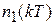. Без учета операции округления его работу можно описать разностным уравнением

,

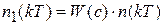где W(c) – операторный коэффициент передачи цифрового фильтра;

n(kT) – преобразованная последовательность чисел; .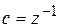

ЦАП осуществляет преобразование кода в напряжение

,

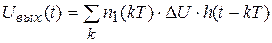где ΔU – шаг преобразования, определяет приращение напряжения на выходе при изменении кода на единицу; h(t - kT) – импульсная характеристика фиксатора.

Если применяется фиксатор нулевого порядка то

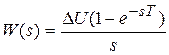
Процесс цифро-аналогового преобразования можно разделить на две операции:

формирование последовательности δ-функций, модулированных входным числом;

подача этих модулированных δ-функций на фильтр, реакцией которого является импульсная характеристика (весовая функция).

Все остальные элементы системы функционируют аналогично непрерывной системе.

Структурная схема аналого-цифровой следящей системы приведена на рис.10.4.

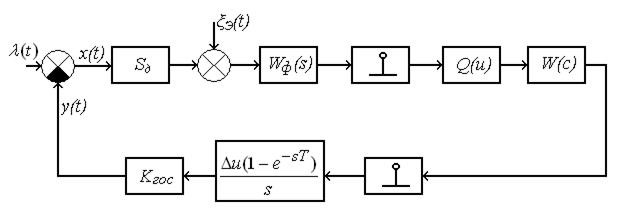
Рис.10.4. Структурная схема аналого-цифровой следящей системы

10.3. Цифровые временные дискриминаторы

При аналого–цифровом преобразовании внутри контура регулирование находит применение схема (рис. 10.5).

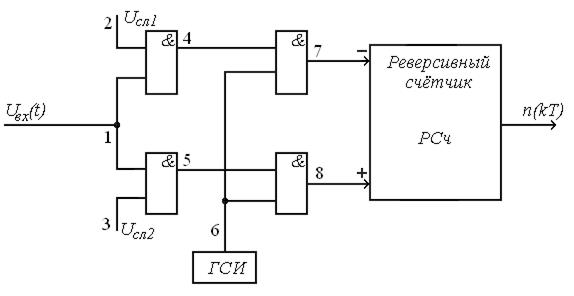
Рис. 10.5. Схема временного дискриминатора

Временные диаграммы работы схемы приведены на рис. 10.6.

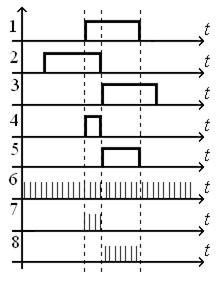
Рис.10.6. Временные диаграммы функционирования дискриминатора

Если временная ошибка слежения равна нулю, то импульсы 4 и 5 будут равной длительности. Величина ошибки пропорциональна разности длительностей импульсов 4 и 5. Для преобразования ошибки в код используется генератор счетных импульсов ГСИ, формирующий частоту заполнения. На выходе реверсивного счетчика формируется код, пропорциональный разности длительностей 4 и 5,т.е. величине ошибки слежения.

Схема, используемая при аналого-цифровом преобразовании вне контура регулирования, приведена на рис. 10.7.

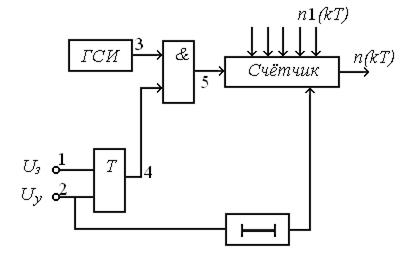
Рис. 10.7. Схема дискриминатора при аналого-цифровом преобразовании вне контура регулирования: U_з – импульс запуска, привязанный по времени к излучаемому сигналу; U_у – импульс приемника.

Перед началом измерения в счетчик заносится оценка задержки, формируемая в фильтре (n₁ ). Счетчик вычисляет разность ,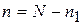

где

;

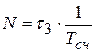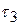─ задержка отраженного импульса; 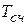─ период счетных импульсов.

Задержанным импульсом, привязанным к сигналу приемника, производится считывание числа n и запись нового значения n₁. Эквивалентная схема приведена на рис. 10.8.

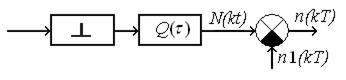
Рис. 10.8. Эквивалентная схема дискриминатора

10.4. Цифровые фазовые дискриминаторы

Из достаточно большого количества существующих схем цифровых фазовых дискриминаторов познакомимся с двумя схемами, формирующими дискриминационные характеристики треугольной и релейной формы.

Фазовый дискриминатор (рис. 10.9) реализован на схеме сумматора по модулю два. Временные диаграммы, поясняющие принцип формирования дискриминационной характеристики, представлены на рис. 10.10.

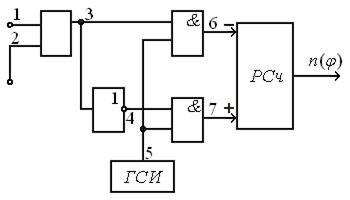
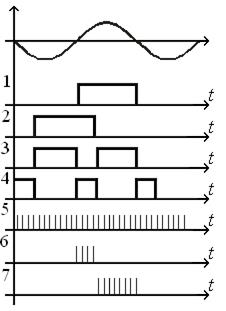
Рис. 10.9. Схема цифрового фазового Рис.10.10. Временные диаграммы

дискриминатора работы дискриминатора

Установившемуся (синфазному) режиму соответствует постоянное фазовое рассогласование между входным и опорным сигналами, равное 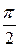, и в контрольной точке 3 длительности импульсов равны длительностям пауз. Чтобы определить разность длительностей импульсов и пауз, пропорциональную величине ошибки, эти длительности преобразуются в код путем их заполнения счетными импульсами, формируемыми генератором счетных импульсов ГСИ. Счетно-импульсный код поступает на реверсивный счетчик РСч, на выходе которого формируется код ошибки.

Эквивалентная схема приведена на рис.10.11. Схема состоит из двух последовательно включенных звеньев: дискретного элемента ДЭ и нелинейного звена с характеристикой n( ).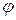

Рис. 10.11. Эквивалентная схема цифрового фазового дискриминатора

Схема и временные диаграммы дискриминатора, формирующего характеристику релейного типа, приведены на рис. 10.12.

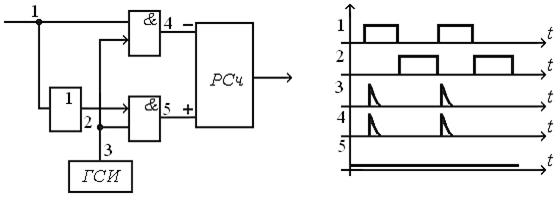
Рис. 10.12. Схема и временные диаграммы функционирования Цифрового фазового дискриминатора релейного типа

Сигнал с выхода квантователя поступает на элементы “И” непосредственно и через инвертор. На другие входы элементов “И” подается последовательность коротких импульсов, следующих с частотой сигнала. В зависимости от знака рассогласования фазы между входным и опорным напряжениями на соответствующий элемент И подается высокий уровень напряжения и на его выход проходят импульсы опорного сигнала.

Формируя релейную характеристику (рис.10.13), дискриминатор определяет только знак фазового рассогласования.

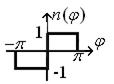
Рис. 10.13. Характеристика дискриминатора релейного типа

Схема дискриминатора, приведенная на рис. 10.14 может использоваться в системах тактовой синхронизации для формирования сигнала тактовой частоты с цель определения границ элементарных посылок цифрового двоичного сигнала.

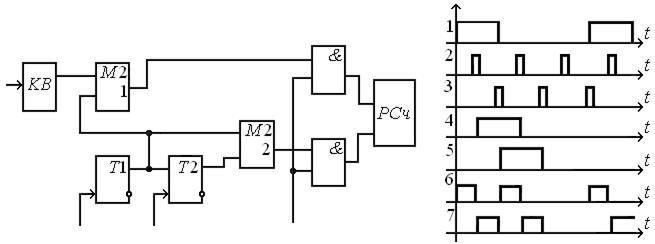
Рис. 10.14. Схема и временные диаграммы функционирования дискриминатора для системы тактовой синхронизации

С помощью триггера Т₁ регенерируется входной сигнал методом стробирования. В синфазном режиме стробирование соответствует середине элементарной импульсной посылки. Информация с Т₁ записывается в Т₂ , таким образом, на выходе Т₁ и Т₂ мы имеем 2 импульсных потока сдвинутых на полтакта. С помощью схем сумматоров по модулю два определяется фазовое рассогласование (эпюры 6,7), преобразуемое в счетно-импульсный код, поступающий на реверсивный счетчик.

10.5. Цифровые частотные дискриминаторы

Известны два типа частотных дискриминаторов:

- цифровая реализация аналогового прототипа дискриминатора с расстроенными контурами;

- частотный дискриминатор, реализующий принцип частотомера или периодомера.

Схема цифрового частотного дискриминатора с расстроенными контурами

приведена на рис. 10.15. +

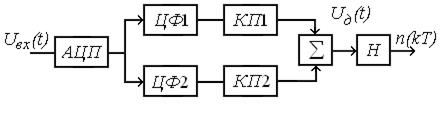
Рис. 10.15. Цифровой частотный дискриминатор

АЦП преобразует сигнал в код.Частота выборки определяется спектром сигнала. Далее сигнал в цифровом виде поступает на два цифровые фильтра со смещенными резонансными частотами, являющиеся аналогом расстроенных контуров; смещение резонансных частот должно обеспечивать необходимую крутизну дискриминационной характеристики.

Рис. 10.16 иллюстрирует формирование дискриминационной характеристики.

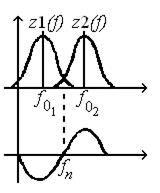
Рис.10.16. Формирование дискриминационной характеристики:

z₁(f) и z₂(f) – модули комплексного сопротивления фильтров

Далее сигнал подается на квадратичные преобразователи, сумматор и накопитель, позволяющий накапливать выборки входного сигнала.

Дискриминатор, использующий принцип счета пересечений нулевого уровня (рис. 10.17) функционирует на принципе частотометра, используя метод счета числа пересечений сигналом нулевого уровня за фиксированный интервал времени и сравнения числа с эталоном.

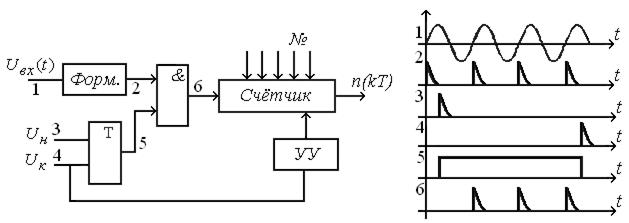
Рис. 10.17. Схема и временные диаграммы работы частотного дискриминатора

Число накапливаемых импульсов на интервале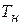

; ; ,

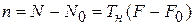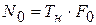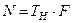где 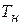– время накопления.

За время 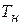подсчитывается число пересечений N и сравнивается с эталонным числом N₀, предварительно записанным в счетчик. Далее код разности чисел считывается со счетчика и подается на цифровой фильтр. Устройство управления обеспечивает сброс счетчика и запись нового числа. Дискрет квантования частоты можно определить следующим образом

Пусть количество импульсов, записанных в счетчик с частотой F_1, равно

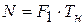, (10.1)

а число импульсов с частотой F₂ равно

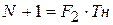(10.2)

Вычтем (10.1) из (10.2):

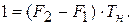(10.3)

Из выражения (10.3) определим дискрет квантования частоты, определяющий точность преобразования частоты в код

= .

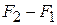
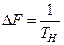Уменьшение дискрета квантования обеспечивается при использовании принципа периодомера, при котором определяется интервал времени соответствующий фиксированному числу периодов входного сигнала посредством заполнения этого интервала счетными импульсами высокой частоты. Затем этот интервал сравнивается с эталонным, соответствующим переходной частоте дискриминатора.

10.6. Цифровые фильтры

Синтез передаточной функции цифрового фильтра. Для синтеза передаточной функции цифрового фильтра часто используется метод дискретизации аналогового фильтра-прототипа.

На основе теории аналоговых фильтров определяется передаточная функция, удовлетворяющая заданным требованиям. Затем производится дискретизация в соответствии с приведенной схемой (рис. 10.18). Непрерывный фильтр преобразуется в дискретную систему путем включения на его входе импульсного элемента и формирующего фильтра. Включение на входе импульсного элемента и формирующего фильтра обеспечивает подобие процессов на выходе цифрового фильтра и аналогового фильтра-прототипа.

Рис. 10.18. Схема дискретизации аналогового фильтра-прототипа

Передаточная функция цифрового фильтра определяется как z-изображение передаточной функции полученного соединения звеньев:

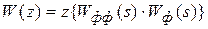
При использовании в качестве формирующего фильтра фиксатора:

; .

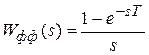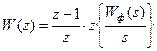Второй метод синтеза на основе использования передаточной функции аналогового фильтра-прототипа состоит в замене операций непрерывного дифференцирования и интегрирования операциями дискретного дифференцирования и интегрирования.

Аналоговое интегрирование производится в соответствии с выражением 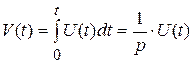, (10.4)

где 1/р ─ оператор интегрирования;

а дискретное интегрирование по методу прямоугольников ─ в соответствии с выражением

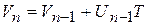, (10.5)

где T – основание прямоугольника (рис. 10.19).

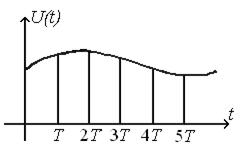
Рис. 10.19. Дискретное интегрирование по методу прямоугольников

Введем оператор запаздывания с, в результате выражение (10.6) запишется в виде:

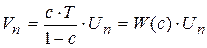, (10.6)

где .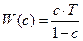

Сравнив (10.4) и (10.6) определим эквивалентные операторы интегрирования и дифференцирования.

Чтобы определить передаточную функцию цифрового фильтра необходимо произвести следующие замены:

- операция дифференцирования ─ ;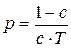

- операция интегрирования ─ .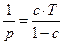

Произведя замену операторов ( 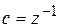), получим соответствие:

.

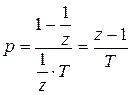Аналогично производится замена переменной s на переменную z в соответствии с равенством

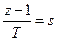
Интегрирование методом трапеций, выполняемое в соответствии с равенством

,

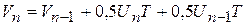также позволяет определить соответствующие операторы.

Реализация цифровых фильтров.Цифровые фильтры могут быть реализованы в прямой, канонической, параллельной и последовательной формах.

Прямая форма базируется на разностном уравнении

,

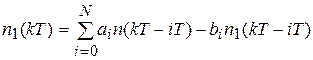где 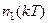– код числа на выходе фильтра; 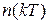– код числа на входе фильтра;

a_i, b_i – коэффициенты.

Структурная схема фильтра представлена на рис. 10.20.

Каноническая форма отличается тем, что для задержки входной и выходной последовательностей используется одна линия задержки.

При последовательной форме реализации сложные звенья или сложная передаточная функция разбивается на ряд простых звеньев, так чтобы каждое звено описывалось дифференциальным уравнением не выше второго порядка. Передаточные функции этих звеньев, включенных последовательно, образуют необходимую передаточную функцию фильтра.

При параллельной форме реализации сложные передаточные функции фильтров формируются как сумма передаточных функций звеньев, включенных параллельно; каждое звено описывается дифференциальным уравнением не выше второго порядка. Каждое из таких элементарных звеньев реализуется по прямой или канонической форме.

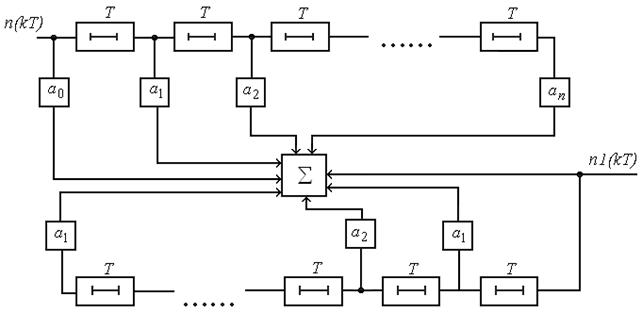
Рис.10.20. Схема цифрового фильтра

В качестве фильтров часто используют реверсивные или обычные двоичные счетчики. При этом используются следующие схемы включения:

- реверсивный счетчик без сброса;

- реверсивный счетчик со сбросом после переполнения;

- реверсивный счетчик с накоплением и сбросом

. Реверсивный счетчик без сброса является цифровым интегратором. Определим его передаточную функцию и операторный коэффициент передачи.

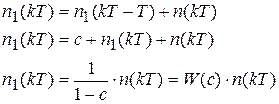
где .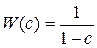

Произведя замену переменной

,

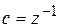получим передаточную функцию

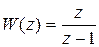
На счетчик с накоплением и сбросом за время 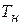на вход поступает r чисел с периодом Т, затем содержимое счетчика сбрасывается. Эквивалентная схема счетчика представляет последовательное соединение элемента с конечной памятью T_H и дискретного элемента (рис. 10.21).

Разностное уравнение, описывающее работу счетчика:

;

,

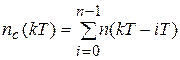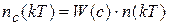где W(c) – передаточная функция:

.

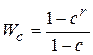Дискретный элемент замыкается через время T_H.

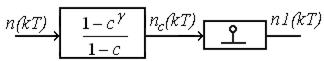
Рис. 10.21. Эквивалентная схема реверсивного счетчика с накоплением и сбросом

10.7. Цифровые генераторы опорного сигнала

Генератор опорного сигнала в цифровых системах фазовой и частотной синхронизации реализует функцию синтезатора частот. Синтезируемая частота определяется выражением

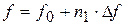, (10.7)

где f – частота выходного сигнала генератора; f₀ – номинальная частота генератора; Δf – дискрет перестройки по частоте;n₁ – код управления, поступающий с выхода фильтра.

Такой генератор может реализован с использованием цифро-аналогового преобразователя и генератора, управляемого напряжением. Недостатком такого генератора, называемого генератором с непосредственным управлением, является невысокая стабильность при обеспечении достаточного диапазона перестройки по частоте. Использование для повышения стабильности кварцевой стабилизации существенно снижает диапазона перестройки.

Поэтому широкое применение нашли генераторы с косвенным управлением частотой, позволяющие избавиться от этого недостатка. При этом можно использовать кварцевую стабилизацию частоты и одновременно обеспечить широкий диапазон перестройки частоты.

Генератор на основе управляемого делителя (рис. 10.22).

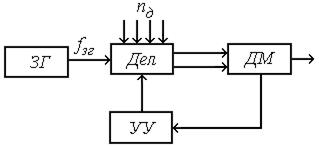
Рис. 10.22. Цифровой управляемый генератор

Дешифратор ДШ определяет нулевое состояние, при этом на выходе формируется импульс, по которому с помощью устройства управления УУ в счетчик записывается число n_д. Если в качестве делителя используется реверсивный счетчик, то импульсы с частотой f_зг поступают на вход вычитания, в результате чего число n_д считывается до нуля. На выходе формируется импульсная последовательность с частотой f:

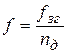. (10.8)

Недостатком является нелинейная зависимость частоты от кода n_д.

Для обеспечения линейной зависимости необходимо производить пересчет управляющего кода. Для определения формулы пересчета приравняем выражения (10.7) и (10.8):

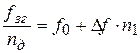. (10.9)

Из выражения (10.9) находим n_д:

.

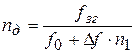Цифровой опорный генератор с управляемым дискретным фазовращателем (рис.10. 23.) Высокостабильный кварцевый задающий генератор формирует последовательность импульсов, которая поступает на вход устройства добавления и исключения импульсов. Исключение или добавление импульса в последовательность приводит к сдвигу фазы на 2π. Уменьшение дискрета подстройки достигается подключением делителя, который формирует опорный сигнал. В результате дискрет подстройки по фазе составит .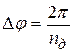

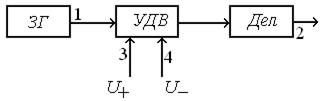
Рис. 10.23. Цифровой опорный генератор с управляемым дискретным фазовращателем

Генератор опорного сигнала для системы слежения за задержкой импульсного сигнала.При использовании в качестве опорного сигнала последовательности следящих импульсов основным элементом опорного генератора является преобразователь код-временная задержка. Этот преобразователь преобразует число n₁ , формируемое в фильтре, во временную задержку следящих импульсов. Преобразование кода во временную задержку реализуется на управляемой линии задержки или счетчике-формирователе. Рассмотрим схему, выполненную на счетчике-формирователе (рис. 10.24).

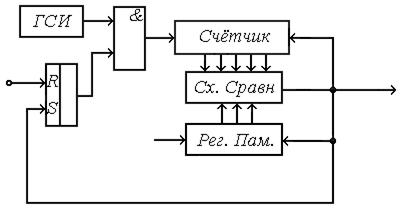
Рис. 10.24. Генератор опорного сигнала для системы слежения за задержкой импульсного сигнала

В регистр памяти записывается код 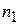, соответствующий оценке задержки.

Синхроимпульсом, связанным по времени с излучением зондирующего импульса, RS – триггер устанавливается в состояние «0». При этом на вход схемы И подается разрешающий уровень напряжения и с генератора счетных импульсов проходят импульсы на вход счетчика. Как только число в счетчике сравнивается с числом 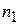(рис.10.25),

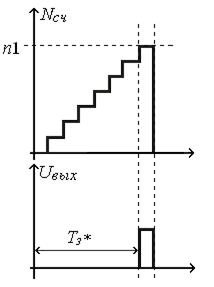
Рис. 10.25. Временные диаграммы

на выходе схемы сравнения формируется импульс запуска генератора следящих импульсов. Этим же импульсом восстанавливается начальное состояние триггера и обнуляется счетчик.

Выходной величиной преобразователя является временной сдвиг запускающих импульсов, равный

Т_з = n₁T_cч,

где T_cч ─ период счетных импульсов, определяющий шаг квантования и точность преобразователя ( см. рис. 10.25).

Цифровой опорный генератор на линии задержки с отводами.Рассмотренные выше схемы опорных генераторов требуют для обеспечения необходимого (достаточно малого) дискрета подстройки, определяющего точность слежения, чтобы частота задающего генератора существенно превышала частоту входного сигнала. Это ограничивает применение схемы при высокой частоте входного сигнала, вследствие ограниченного быстродействия элементной базы. Ниже рассматриваются схемы опорных генераторов, позволяющие расширить частотный диапазон применения.

Опорный генератор на линии задержки с отводами (рис. 10.26) обеспечивает формирование опорного сигнала с частотой, равной частоте задающего генератора.

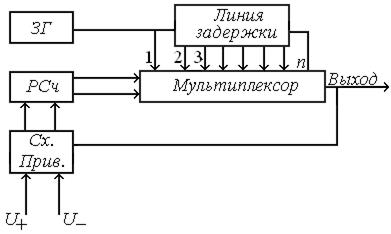
Рис. 10.26.

Параметры линии задержки определяются соотношениями:

;

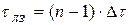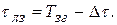
Дискрет подстройки фазы равен .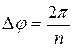

На выходах линии задержки формируется многофазная импульсная последовательность (рис. 10.27).

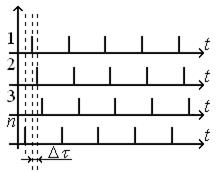
Рис. 10.27. Многофазная импульсная последовательность

Мультиплексор коммутирует импульсную последовательность в соответствии с адресом, поступившим с реверсивного счетчика. Схема привязки обеспечивает привязку момента смены показаний счетчика к выходному сигналу (для предотвращения их совпадения).

В анализируемой схеме задержка формируется по закону унитарного кода

Рассмотрим схему, в которой формирование задержки производится по принципу позиционной системы счисления. Величина дискрета задержки в разрядах (вес разряда) определяется положением разряда, а количество дискретов задержки в разряде – выбранным основанием (базисом).

Пусть = ,

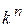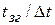где 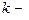выбранный базис системы счисления; n ─ число разрядов позиционного кода. Суммарная задержка ( 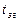- 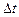) может быть набрана с помощью последовательно включенных n линий задержки. Дискрет задержки каждой последующей линии возрастает пропорционально выбранному базису 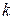. Дискрет коррекции фазы опорного сигнала определяется величиной дискрета задержки 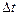первой линии, образующей младший разряд. Задержка первой линии равна 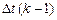. Дискрет задержки второй линии ─ 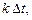а суммарная задержка ─ 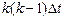и т.д. Дискрет задержки n-й линии равен 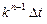, а суммарная величина задержки ─ 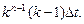Необходимая величина относительной нестабильности линии задержки составляет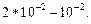

Схема дискретного фазовращателя приведена на рис.10.28.

Задающий генератор генерирует сигнал стабильной частоты. С помощью элементов задержки и переключателей производится задержка сигнала задающего генератора по закону управляющего кода. В качестве переключателей могут быть использованы элементы 2И-ИЛИ. Реверсивный счетчик предназначен для формирования управляющего кода. Запоминающее устройство обеспечивает хранение управляющего кода и привязку моментов его изменения к выходным сигналам элементов задержки, что исключает возможность переключения входов и выходов элементов задержки в момент присутствия на входах переключателей сигналов.

Дискрет подстройки фазы управляемого сигнала равен 2 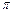/ 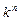. Объем оборудования, необходимый для построения цифрового фазовращателя, определяется в основном числом отводов, являющихся входами мультиплексоров. Число входов определяет сложность мультиплексоров, коэффициенты пересчета счетчиков, формирующих управляющий код. В соответствии с этим критерием оптимальным является дискретный фазовращатель с линией задержки сформированной по принципу формирования двоичного кода.

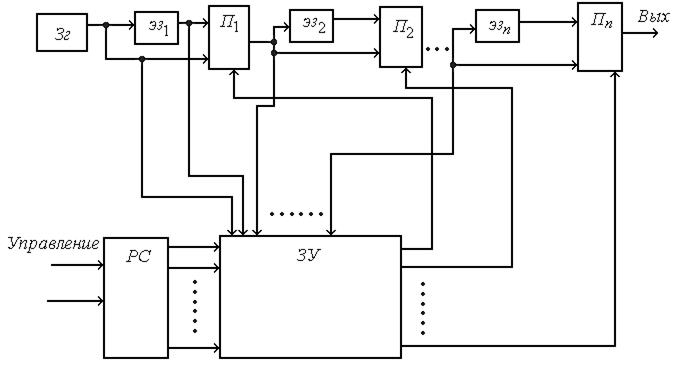
Рис.10.28. Функциональная схема дискретного фазовращателя:

Зг - задающий генератор; Эз1,…,Эзn – элементы задаржки; П1,…,Пn – переключатели; РС – реверсивный счетчик; ЗУ – запоминающее устройство.

Рассмотренные технические решения обеспечивают работу задающего генератора на частоте входного сигнала, что позволяет существенно расширить частотный диапазон применения ЦСФС . Однако для реализации систем необходимо наличие линий задержки с широким перечнем номиналов. Использование аналоговых линий задержки, кроме того требует применения схем согласования со входами цифровых элементов.

Формирование опорного сигнала методом временной трансформации.Рассмотрим сущность метода, иллюстрируемого схемой (рис.10.29)

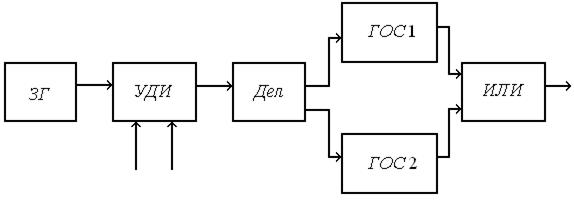
Рис.10.29. Схема опорного генератора: ЗГ – задающий генератор; УДИ – устройство добавления-исключения; Дел – делитель; ГОС 1, ГОС 2 – генераторы опорного сигнала; ИЛИ – логический элемент.

Из высокостабильного сигнала задающего генератора ЗГ делением его частоты формируется управляемый синхросигнал, которым периодически фазируются коммутируемые генераторы опорного сигнала (ГОС). Фаза управляемого сигнала корректируется с помощью УДВ. В качестве ГОС используются генераторы ударного возбуждения, запуск которых производится по срезу управляемого синхросигнала, а гашение колебаний – по фронту. ГОС генерирует сигнал при наличии на управляющем входе уровня логического нуля.

Частоты опорного сигнала (ОС) и сигнала задающего генератора определяются одним из следующих соотношений:

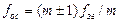(10.10)

или

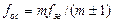, (10.11)

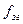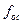где m>>1, число, определяющее величину дискрета подстройки. Пусть соотношения частот и определяются выражением

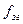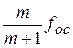= или 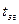= 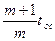, (10.12)

где 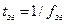─ период сигнала ЗГ; 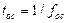─ период ОС.

Период регулирования формируется путем деления импульсной последовательности задающего генератора на 2m. При этом период синхросигнала при отсутствии коррекции равен 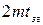, а период регулирования ГОС – 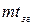, т.е.

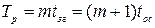(10.13)

Таким образом, при выполнении соотношений (10.3),(10.4) период синхросигнала равен целому числу (m) периодов сигнала ЗГ и целому числу ( 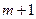) периодов ОС.

Поэтому при отсутствии импульсов коррекции на входе УДИ периодическое фазирование ГОС синхросигналом не приведет к разрыву фазы опорного сигнала.

Добавление с помощью УДИ импульса коррекции в последовательность, формируемую ЗГ, приведет к уменьшению периода регулирования на величину :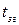

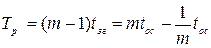. (10.14)

Как следует из соотношения (10.6), уменьшение 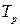в единицах периода ГОС составит:

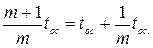(10.15)

Поскольку фаза ОС жестко «привязана» к фронту синхросигнала, то изменение периода следования последнего на величину 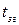приведет к сдвигу на опережение временного положения фронта синхросигнала относительно нулевой фазы ОС, в силу периодичности ОС, как следует из (2.6), на величину:

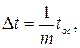
что соответствует сдвигу по фазе опорного сигнала на дискрет, равный .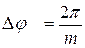

Вычитание импульса из последовательности ЗГ приведет к увеличению периода регулирования на :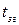

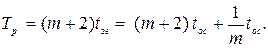
что приведет к сдвигу на отставание временного положения фронта синхросигнала относительно нулевой фазы ОС на величину

-

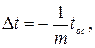
что соответствует сдвигу по фазе опорного сигнала на дискрет, равный .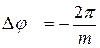

В качестве фазируемых ГОС могут быть использованы генераторы ударного возбуждения, поочередно коммутируемые синхросигналом, генераторы прямоугольных импульсов, в том числе генераторы релаксационного типа. Необходимость фазирования внешним сигналом, обеспечения малой длительности переходных процессов, простоты реализации предполагают использование ГОС с невысокими требованиями к их стабильности.

Требования к стабильности частоты генераторов.Определим требования к стабильности ГОС.

Пусть 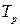определяется выражением (10.5). Тогда на временном интервале, равном 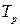ГОС работает в режиме свободных колебаний. При этом «набег» фазы ОС относительно ЗГ 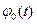обусловленный взаимной нестабильностью частот 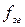и 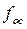растет по линейному закону.

Периодическая функция 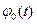может быть определена следующим образом:

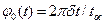, при 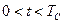, (10.16)

где 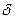- взаимная нестабильность частот 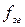и 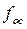. При высокой стабильности задающего генератора величина 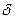определяет относительную нестабильность ГОС.

Максимальный набег фазы на интервале периода регулирования составит величину

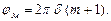
Среднее значение процесса 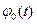и дисперсию 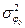найдем усреднением 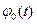по времени.

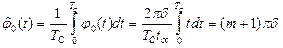; (10.17)

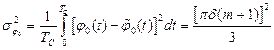. (10.18)

Среднеквадратическое отклонение «набега» фазы:

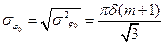. (10.19)

Максимальное отклонение относительно среднего значения равно

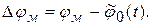
Таким образом, максимальное отклонение набега фазы относительно среднего значения равно

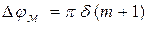
Интенсивность флуктуаций фазы относительно среднего значения в отсутствие шумов на входе определяет ошибку синхронизации в системе, построенной на основе анализируемого цифрового управляемого генератора, поскольку в стационарном режиме система отслеживает среднее значение.

Известно, что максимальная ошибка синхронизации ЦСФС, обусловленная дискретностью коррекции фазы в отсутствие шумов на входе равна величине дискрета подстройки фазы (2 ).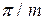

Приняв величину 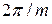за максимально допустимое отклонение относительно среднего значения:

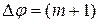
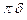
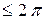/m,

определим допустимую нестабильность частоты ГОС

,

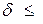
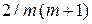где 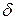– относительная нестабильность частот ЗГ и ГОС.

Выполнение этого условия позволит при расчете динамической ошибки слежения учитывать нестабильность задающего генератора.

Расчетные величины относительной нестабильности представлены в табл. 10.1. Выполнение этого условия позволит в формуле для расчета динамической ошибки слежения учитывать нестабильность задающего генератора.

Результаты расчета показывают, что приемлемая точность может быть достигнута при относительной нестабильности