Дискретные системы радиоавтоматики

9.1. Системы с прерывистым входным сигналом. Функциональные схемы

В радиотехнических системах часто в качестве носителя информации используют импульсный сигнал (импульсные РЛС, сканирование диаграммы направленности или переключение процесса слежения с одного объекта на другой и т.д.). В этом случае на вход дискриминатора поступает периодический импульсный сигнал (рис.9.1).

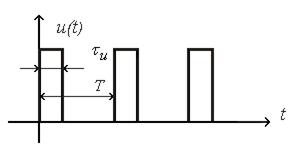
Рис.9.1. Импульсный сигнал на входе дискриминатора

Функциональные схемы следящих систем при наличии прерываний входного сигнала приведены на рис.9.2, 9.3. Схема (рис.9.2) отличается от обобщенной функциональной схемы радиоэлектронной следящей системы наличием ключа Кл, размыкаемого во время пауз. На рис. 9.3 представлена схема с фиксатором, который препятствует пропаданию напряжения на входе фильтра в промежутке между импульсами.

Рис. 9.2. Функциональная схема следящей системы с прерывистым входным сигналом: Дис – дискриминатор; ОГ – опорный генератор

Фиксатор ( экстраполятор нулевого порядка ) состоит из сумматора 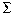, линии задержки на время 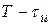и интегратора Инт. В фиксаторе во время действия импульса полезного сигнала на входе интегратор заряжается до некоторого уровня, который сохраняется до прихода очередного импульса. Перед приходом очередного импульса интегратор разряжается задержанным на время 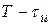отрицательным импульсом, поступающим через линию задержки.

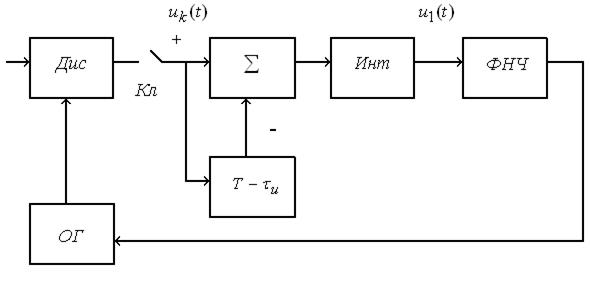
Рис. 9.3. Функциональная схема следящей системы с фиксатором

Временные диаграммы, поясняющие принцип работы фиксатора, приведены на рис.9.4.

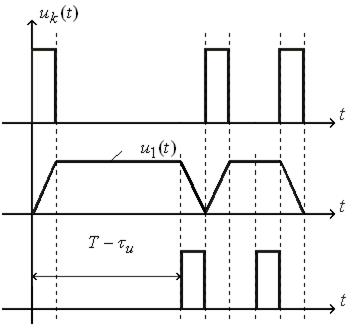
Рис. 9.4. Временные диаграммы, поясняющие принцип работы фиксатора

Использование фиксатора позволяет обеспечить необходимый коэффициент усиления контура.

Передаточная функция фиксатора:

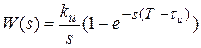(9.1)

Если ,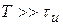

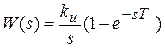, (9.2)

где ─ коэффициент передачи интегратора (величина обратная постоянной времени).

9. 2. Структурные схемы систем

Структурная схема системы с прерывистым входным сигналом без фиксатора отличается от схемы системы с непрерывным входным сигналом наличием ключа перед звеном с передаточной функцией W_ф(р) (рис. 5). При использовании фиксатора схема дополняется звеном с передаточной функцией, определяемой выражениями (9.1) или (9.2).

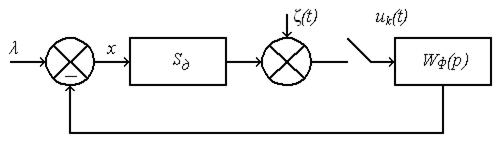
Рис. 9.5. Структурная схема системы с прерывистым входным сигналом:

─ крутизна дискриминационной характеристики; 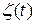─ флюктуационная составляющая

Коэффициент передачи ключа (рис. 9.6)

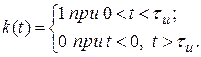
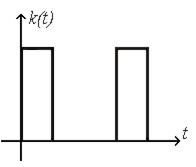
Рис. 9.6. Коэффициент передачи ключа

Наличие ключа делает процесс регулирования прерывистым, а системы – системами с переменными во времени параметрами.

Анализ таких систем определяется соотношениями между длительностью импульса, полосой пропускания следящей системы и частотой повторения импульсов.

Если частота повторения импульсов много больше полосы системы, то анализ может быть осуществлен методами анализа непрерывных систем.

Если же это условие не выполняется и за время происходит значительное изменение ошибки слежения, то такие системы называют системами с конечным временем съема данных, или импульсными системами. Анализ их осуществляется отдельно в момент отсутствия и наличия сигнала на входе, затем решения сшиваются.

Если же за время 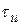ошибка меняется незначительно, анализ системы можно существенно упростить, представив систему прерывистого регулирования как дискретную. Дискретными называют системы, в которых сигналы подвергаются дискретизации по времени.

Рассмотрим методику перехода к дискретной системе на примере системы прерывистого регулирования без фиксатора.

Чтобы получить структурную схему дискретной системы, вместо ключа вводят импульсный элемент (рис. 9.7), коэффициент передачи которого является последовательностью дельта-функций

.

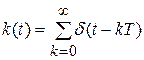Рис. 9.7. Изображение импульсного элемента на структурной схеме

Импульсный элемент преобразует непрерывную функцию в последовательность модулированных по площади дельта-функций:

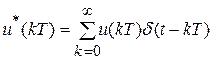, (9.3)

где 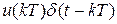─ модулированная по площади дельта-функция (рис. 9.8);

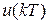─ дискретная функция (рис. 9.9).

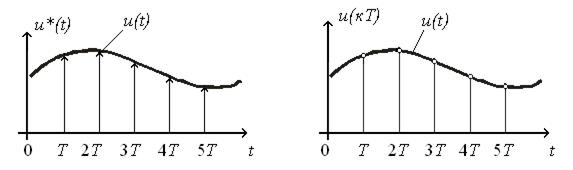
Рис. 9.8. Модулированная Рис. 9.9. Дискретная функция

последовательность дельта-функций

Дискретная функция в тактовых точках равна исходной непрерывной, а в промежутках между тактовыми точками равна нулю (см. рис.9.9).

Импульсный элемент преобразует непрерывную функцию в дискретную и модулирует ее по площади.

Импульсы напряжения на выходе ключа имеют конечную длительность, и коэффициент передачи его равен единице в замкнутом состоянии, а на выходе импульсного элемента формируется последовательность дельта-функций.

Чтобы обеспечить подобие процессов на выходе ключа и выходе заменяющего его импульсного элемента, необходимо последовательно с импульсным элементом включить формирующий фильтр.

Импульсная характеристика формирующего фильтра 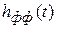─ реакция системы на последовательность дельта-функций. Она должна быть равна коэффициенту передачи ключа:

.

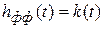Передаточная функция формирующего фильтра является преобразованием Лапласа от импульсной характеристики:

.

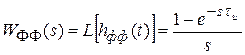Процесс ее формирования можно представить как преобразование Лапласа разности двух ступенчатых функций (разность изображений по Лапласу единичной ступенчатой функции и этой же функции, задержанной на длительность импульса).

Условием эквивалентности ключа и импульсного элемента с формирователем является незначительное изменение ошибки в моменты действия импульса.

С учетом проведенных преобразований структурная схема может быть представлена в виде рис. 9.10.

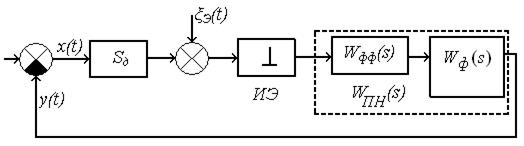
Рис. 9.10. Структурная схема дискретной системы

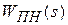называется передаточной функцией приведенной непрерывной части системы:

;

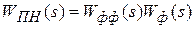при наличии фиксатора передаточная функция звена

.

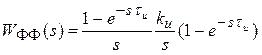Если 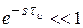, то 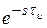можно приближенно записать в виде

;

.

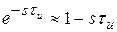Обычно полагают, что .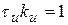

Тогда

.
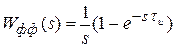Эквивалентная флюктуационная составляющая отличается от флюктуационной составляющей непрерывной системы. Ее дисперсия равна

.

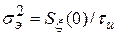Таким образом, в дискретной системе закон изменения параметров определяется только периодом повторения импульсов.

9.3. Математическое описание дискретных систем

9.3.1. Z-преобразование и его свойства

Для описания и анализа дискретных систем используется соответствующий математический аппарат: интегрирование заменяется суммированием, дифференцирование – конечной разностью, вместо дифференциальных уравнений используются разностные уравнения. Наряду с разностными уравнениями при анализе систем используются также дискретные преобразования Фурье и Лапласа, z-преобразование и другие.

Дискретное преобразование Лапласа:

,

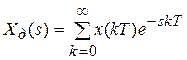где 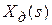─ изображение; 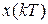─ оригинал.

Для анализа систем преобразование Лапласа неудобно, так как изображение является трансцендентной функцией переменной. Поэтому путем замены переменной

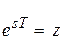
переходят к z-преобразованию:

.

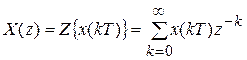Основные свойства z-преобразования определяются рядом теорем:

- теорема обращения, позволяющая по изображению определить оригинал: ;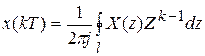

- z-изображение суммы или разности дискретных процессов:

;

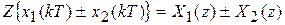- z-изображение произведения постоянной величины и дискретного процесса:

;

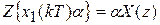- теорема о конечном значении оригинала:

;

- теорема о начальном значении оригинала:

;

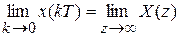- теорема свертки оригиналов:

;

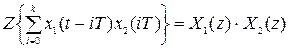- теорема запаздывания: при ненулевых начальных условиях ─

; ;

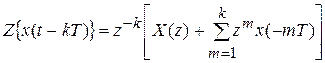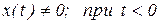при нулевых начальных условиях ─

;

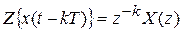- z- преобразование непрерывной функции времени:

,

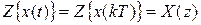где 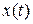─ непрерывная величина.

Z-преобразование изображения по Лапласу непрерывного процесса по определению совпадает с z-преобразованием процесса :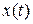

;

,

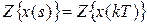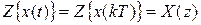где 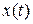─ непрерывная величина.

Таким образом,

.

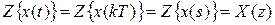9.3.2. Передаточные функции дискретных систем

Передаточная функция дискретной системы определяется как отношение z-изображений выходной и входной величин при нулевых начальных условиях:

; .

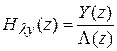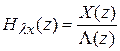Передаточные функции дискретной системы (рис. 9.10) при нулевом значении флюктуационной составляющей определяются выражениями

; (9.4)

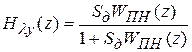. (9.5)

Если в системе используется фиксатор, то передаточная функция приведенной непрерывной части системы определяется выражением

,

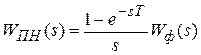где 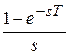─ передаточная функция последовательного соединения фиксатора и формирующего фильтра.

;
.

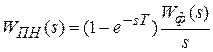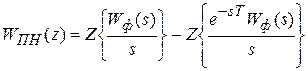Умножение изображения по Лапласу на 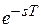соответствует задержке оригинала на величину Т. С учетом теоремы сдвига и обозначения

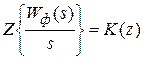(9.6)

получим

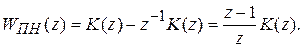(9.7)

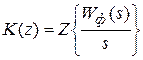─ определяется по таблицам z- изображений.

9.3.3. Разностные уравнения

Разностные уравнения определяют связь между дискретными значениями выходной и входной величин в тактовых точках.

Чтобы составить разностное уравнение, надо представить дискретную передаточную функцию в следующем виде:

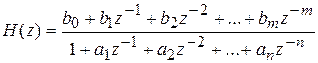. (9.8)

Если ─ значение выходной величины, а 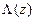─ входной в виде

z-изображения, то связь между ними определяется выражением

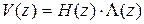. (9.9)

Подставим (9.8) в (9.9):

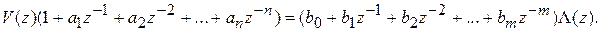
(9.10)

Применим к левой и правой частям уравнения (9.10) теорему обращения. С учетом теоремы запаздывания оригинала можно записать

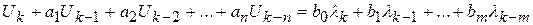, (9.11)

где ;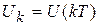

.

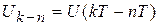Из уравнения (9.11) можно определить значения оригинала в тактовых точках:

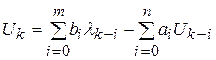. (12)

Уравнение (9.12) является разностным уравнением, определяющим связь между входной и выходной величинами в тактовых точках.

9.3.4. Операторный коэффициент передачи дискретной системы

Для составления операторного коэффициента передачи вводится оператор запаздывания – с.

Действие его на временную функцию приводит ее к сдвигу по времени на величину Т :

;

;

…………………………

.

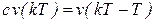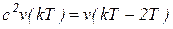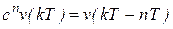При использовании оператора с разностное уравнение записывается в виде

,

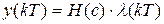где

.

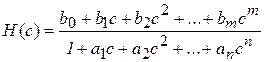Чтобы перейти от дискретной ПФ к операторному коэффициенту передачи, необходимо сделать замену:

.

9.3.5. Комплексный коэффициент передачи дискретной системы

Комплексный коэффициент передачи дискретной системы (частотную передаточную функцию) можно получить из передаточной функции дискретной системы путем замены :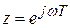

.

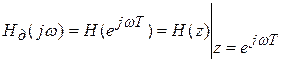Комплексный коэффициент передачи дискретной системы определяется как отношение комплексных амплитуд управляемой величины Y(kT) и задающего воздействия в тактовых точках kT. По формированию значений выходного процесса в тактовых точках дискретная система эквивалентна непрерывной с комплексным коэффициентом передачи H_д(jw).

Комплексный коэффициент передачи является периодической функцией переменной 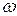с периодом изменения, равным

.

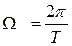9.3.6. Устойчивость дискретных систем

Устойчивость дискретной системы связана с расположением полюсов ее передаточной функции на комплексной плоскости. Если все полюса расположены в левой полуплоскости, система устойчива. Таким образом, заменив в передаточной функции H(z) z на e^sT и решив характеристическое уравнение, можно определить устойчивость.

При переходе от s-плоскости к z-плоскости левая полуплоскость плоскости s трансформируется в круг единичного радиуса. Поэтому дискретная система устойчива, если полюсы ее передаточной функции H(z) расположены внутри окружности единичного радиуса, т.е. удовлетворяют условию

|z_i| < 1 , i = 1,2… n,

где z_i ─ корни характеристического уравнения:

A(z) = a_n zⁿ + a_n-1z ^n-1 + …+ a₀ = 0.

Характеристическое уравнение составляется путем приравнивания к нулю знаменателя передаточной функции:

.

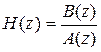Для определения устойчивости дискретных систем используют алгебраические и частотные критерии.

Алгебраический критерий состоит в проверке выполнения системы неравенств, составленных из коэффициентов характеристического уравнения.

При n = 1: .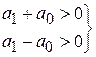

При n = 2: .

При n=3 указанная система неравенств принимает вид

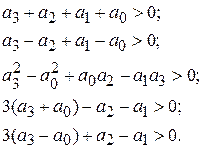
Частотный критерий (критерий Найквиста): если годограф комплексного коэффициента передачи разомкнутой системы при изменении частоты от 0 до 2π/Т не охватывает точку c координатами (-1; j0), то система устойчива.

Проанализируем устойчивость системы, представленной структурной схемой (рис. 9.11).

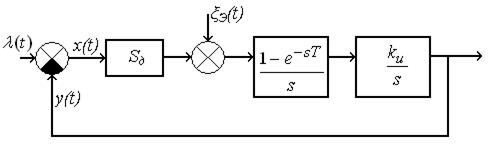
Рис. 9.11. Структурная схема дискретной системы

Передаточная функция от воздействия к ошибке

,

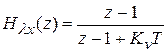Характеристическое уравнение:

.

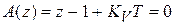Учитывая общую форму записи характеристического уравнения ,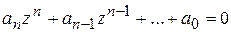

найдем коэффициенты

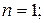
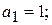
Условие устойчивости для систем с n = 1:

Таким образом, в дискретной системе накладываются ограничения на период дискретизации Т и на коэффициент усиления K_v.

Непрерывная система с одним интегратором не имеет таких ограничений.

Пусть 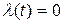при t = 0, а на выходе интегратора имеется напряжение U, равное х(0); тогда при t = 0 получим:

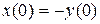– на входе интегратора;

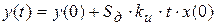– на выходе интегратора.

Соответственно

,

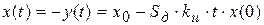а через такт, при t = T:

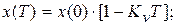
График зависимости х(t) приведен на рис. 9.12.

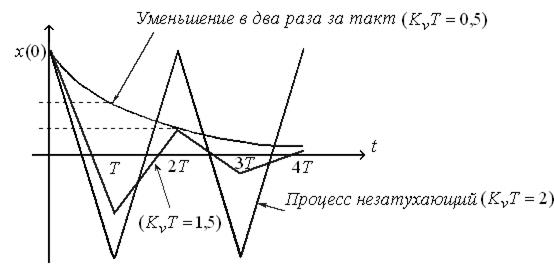
Рис. 9.12. Графики изменения ошибки в переходном режиме

9.3.7.Анализ детерминированных процессов в дискретных системах

Задачей анализа является определение динамической ошибки 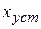или зависимости выходной величины от входной. Анализ может быть произведен с помощью z-преобразований.

Если имеем z-изображение

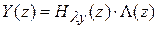
и необходимо определить оригинал по z-изображению выходной величины, то можно воспользоваться теоремой обращения:

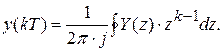
Для вычисления интеграла обращения используют теорему о вычетах, в соответствии с которой для простого полюса

.

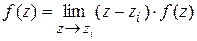Для полюса порядка m:

.

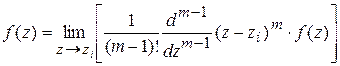Для определения установившегося значения величины используют теорему о предельном значении оригинала:

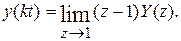
В некоторых случаях можно использовать таблицы, если выражение, определяющее z-изображение, простое, или разложить его на простые слагаемые и затем использовать таблицы.

Для определения реакции системы на детерминированное воздействие можно также использовать разностное уравнение. При высоком порядке разностного уравнения для его решения применяют вычислительные средства.

9.3.8. Анализ случайных процессов дискретных систем

Наиболее часто используемой характеристикой является дисперсия случайного процесса, в частности, дисперсия ошибки слежения. Дисперсия выходного процесса в тактовых точках (t= kT ) и стационарном случайном воздействии u(t) на входе с известной корреляционной функцией и спектральной плотностью S(w) определяется выражением

.

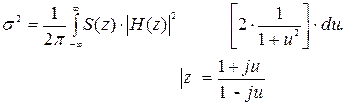Подынтегральное выражение является дробно-рациональной функцией переменной jw. Вычисление интеграла производится по методике, используемой при расчете дисперсии в линейных непрерывных системах.