Анализ качественных характеристик следящей системы
5.1.Показатели качества следящей системы
Качество работы следящей системы оценивается следующими показателями качества: точности, запаса устойчивости и быстродействия.
По переходной характеристике могут быть оценены : быстродействие и перерегулирование, определяющее запас устойчивости.
Перерегулирование определяется как относительная величина максимального отклонения управляемой величины y(t) от установившегося значения в переходном процессе (рис. 5.1):
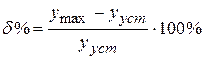 .
.
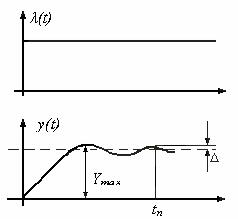
Рис.5.1. Переходная характеристика
Рекомендуемые значения перерегулирования составляют (10…30) %. Дополнительно к величине перерегулирования иногда задается число колебаний на длительности переходного процесса (от 1-2 до 3-4). По числу колебаний может быть качественно оценен запас устойчивости.
Быстродействие системы оценивается длительностью переходного процесса. Длительность переходного процесса – интервал времени от момента подачи на вход системы единичного сигнала, до момента, после которого выполняется неравенство (5.1).
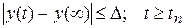 ; (5.1)
; (5.1)
где 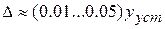 .
.
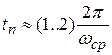 ; (5.2)
; (5.2)
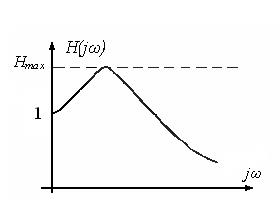
Рис. 5.2. Амплитудно-частотная характеристика замкнутой системы
К частотным показателям качества относятся: запас устойчивости по фазе и амплитуде и показатель колебательности. Показателем колебательности называют абсолютный максимум АЧХ замкнутой системы (рис.5.2), отнесенный к ее значению на нулевой частоте. Для систем, содержащих интегрирующие звенья, у которых Н(0) = 1, показателем колебательности является абсолютный максимум АЧХ (рис. 5.2):
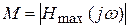 .
.
Рекомендуемые значения показателя колебательности - 1,1…1.5.
5.2. Анализ установившейся (динамической) ошибки
Оценка показателей качества следящей системы производится при следующих типовых воздействиях:
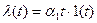 - линейное;
- линейное;
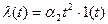 - квадратичное;
- квадратичное;
 - полиномиальное.
- полиномиальное.
Линейное воздействие имеет место, в частности, в системе слежения за задержкой при слежении за объектом, перемещающимся с постоянной радиальной скоростью, в системе ФАПЧ при постоянной частотной расстройке входного и опорного сигналов.
Квадратичное – при слежении за объектом, перемещающимся с ускорением, в системе ФАПЧ – при линейно изменяющейся частотной расстройке и т.д.
При проектировании систем возникает необходимость оценки ошибки слежения в установившемся режиме при полиноминальном входном воздействии, являющемся аппроксимацией реальных воздействий на ограниченном интервале времени. В зависимости от вида передаточной функции фильтра системы эта ошибка может иметь конечное значение или изменяться с течением времени.
Если ошибка имеет конечное установившееся значение, для ее оценки используют теорию преобразований Лапласа, в частности, теорему о предельном значении оригинала:
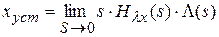 ,
,
где 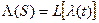 ;
; 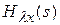 - передаточная функция от воздействия к ошибке.
- передаточная функция от воздействия к ошибке.
Если ошибка изменяется с течением времени, для ее расчета используется метод разложения ошибки по производным входного воздействия. Рассмотрим этот метод.
Величина 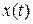 может быть определена с помощью интеграла свертки:
может быть определена с помощью интеграла свертки:
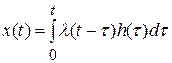 . (5.3)
. (5.3)
Передаточная функция связана с весовой функцией преобразованием Лапласа:
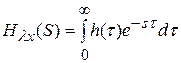 . (5.4)
. (5.4)
Представим задающее воздействие степенным рядом с ограниченным числом членов:

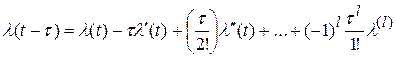 . (5.5)
. (5.5)
Подставив формулу (5.5) в (5.3), получим:
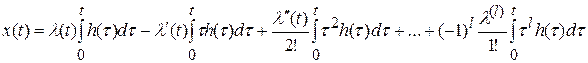 . (5.6)
. (5.6)
Если 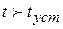 (
( 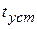 ─ длительность переходного процесса), то в этом случае
─ длительность переходного процесса), то в этом случае 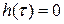 и можно заменить верхний предел интегралов в (5.6) на бесконечность, поскольку увеличение предела не изменяет значения интеграла. Тогда (5.6) можно записать в виде:
и можно заменить верхний предел интегралов в (5.6) на бесконечность, поскольку увеличение предела не изменяет значения интеграла. Тогда (5.6) можно записать в виде:
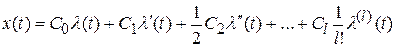 , (5.7)
, (5.7)
где 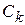 – коэффициенты ошибки:
– коэффициенты ошибки:
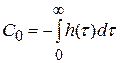 ;
; 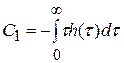 ;
; 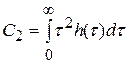 ;
; 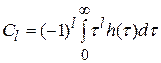 .
.
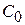 - коэффициент ошибки по положению;
- коэффициент ошибки по положению;
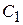 - коэффициент ошибки по скорости;
- коэффициент ошибки по скорости;
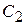 - коэффициент ошибки по ускорению;
- коэффициент ошибки по ускорению;
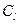 - коэффициент ошибки по l-ой производной входного воздействия.
- коэффициент ошибки по l-ой производной входного воздействия.
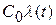 - ошибка по положению;
- ошибка по положению; 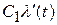 - ошибка по скорости;
- ошибка по скорости;
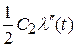 - ошибка по ускорению.
- ошибка по ускорению.
Нетрудно видеть, что
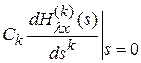 .
.
5.3. Понятие астатизма системы
С величиной коэффициентов ошибки связано понятие астатизма системы
Порядок астатизма системы определяется индексом первого, отличного от нуля коэффициента ошибки. Если 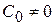 система обладает астатизмом 0-го порядка и называется статической, если
система обладает астатизмом 0-го порядка и называется статической, если 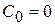 ;
; 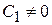 ─ система обладает астатизмом 1-го порядка.
─ система обладает астатизмом 1-го порядка.
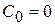 ;
; 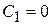 ;
; 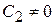 - система с астатизмом 2-го порядка и т. д.
- система с астатизмом 2-го порядка и т. д.
Астатические системы обладают следующим свойством: если на вход системы с астатизмом k-го порядка подается входное воздействие, описываемое полиномом k-ой степени, значение ошибки в установившемся режиме постоянно и не равно нулю.
Если порядок астатизма больше степени полинома, установившееся значение ошибки равно нулю ( 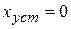 ). Если порядок астатизма меньше степени полинома, определяющего задающее воздействие, ошибка изменяется с течением времени и в пределе будет равна бесконечности.
). Если порядок астатизма меньше степени полинома, определяющего задающее воздействие, ошибка изменяется с течением времени и в пределе будет равна бесконечности.
Порядок астатизма определяется числом интегрирующих звеньев в контуре следящей системы. Следовательно, для уменьшения ошибки необходимо увеличивать количество интегрирующих звеньев. Но это увеличение имеет ограничение, так как с увеличением числа звеньев ухудшается устойчивость системы (каждое интегрирующее звено вносит фазовый сдвиг, равный 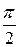 ). Поэтому для систем, имеющих порядок астатизма выше второго, для обеспечения устойчивости необходимо использовать специальные методы коррекции.
). Поэтому для систем, имеющих порядок астатизма выше второго, для обеспечения устойчивости необходимо использовать специальные методы коррекции.
Порядок астатизма также зависит от точки приложения воздействия (рис. 5.3).
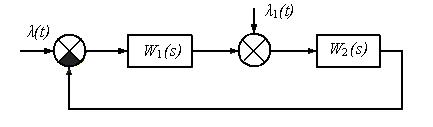
Рис. 5.3. К определению порядка астатизма системы
Если астатизм определяется по отношению к воздействию 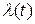 , то его порядок определяется суммой интегрирующих звеньев в
, то его порядок определяется суммой интегрирующих звеньев в 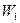 (s)и
(s)и 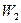 (s).
(s).
Относительно 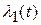 порядок астатизма определяется числом интегрирующих звеньев в
порядок астатизма определяется числом интегрирующих звеньев в 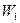 (s) и не зависит от их числа в
(s) и не зависит от их числа в 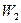 (s). Соответствующие передаточные функции, связывающие задающее воздействие и ошибку слежения, определяются выражениями
(s). Соответствующие передаточные функции, связывающие задающее воздействие и ошибку слежения, определяются выражениями
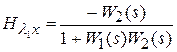 ;
; 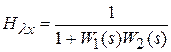 .
.
Таким образом, порядок астатизма системы определяется числом интегрирующих звеньев, включенных в цепь обратной связи между точкой приложения воздействия и точкой измерения ошибки слежения.
5.4. Методы вычисления коэффициентов ошибки
Представим передаточную функцию 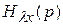 в виде
в виде
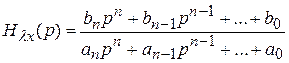 . (5.8);
. (5.8);
В разложении ошибки по производным входного воздействия
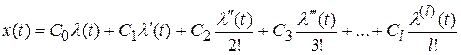
заменим операцию дифференцирования символом р , т.е. 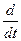 = p и вынесем формально общий множитель
= p и вынесем формально общий множитель 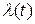 за скобки:
за скобки:
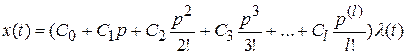 (5.9);
(5.9);
С другой стороны 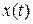 можно определить дифференциальным уравнением, записанным в сокращенной форме:
можно определить дифференциальным уравнением, записанным в сокращенной форме:
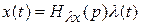 . (5.10)
. (5.10)
Подставив (5.8) в (5.10), приравняем выражения (5.9) и (5.10) 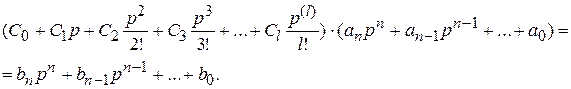 (5.11)
(5.11)
Приравняв слагаемые, имеющие одинаковые степени р в правой и левой частях (5.11), получим:
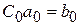 ;
; 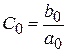 ;
;
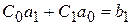 ;
; 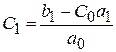
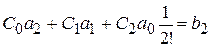 ;
; 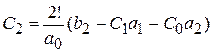 .
.
На основании полученных выражений можно записать формулу для расчета коэффициентов ошибки:
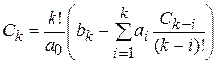 . (5.12)
. (5.12)
Коэффициенты ошибки могут быть также вычислены по формулам, составленным из коэффициентов полиномов числителя и знаменателя передаточной функции разомкнутой системы:
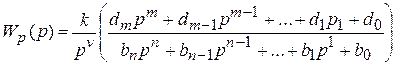 , (5.13)
, (5.13)
где k – добротность системы ; v – порядок астатизма.
Приведенные в табл. 5.1 формулы получены по вышеизложенной методике подстановкой в выражение
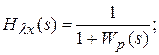
передаточной функции разомкнутой системы в виде (5.13).
5.5. Динамические ошибки в следящих системах с астатизмом различного порядка
Для анализа используем обобщенную структурную схему (рис. 5.4).

Рис. 5.4. Обобщенная структурная схема следящей системы
В качестве фильтров используем пропорционально-интегрирующий фильтр (рис. 5.5) с последовательно включенным интегратором:
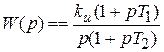 (5.14)
(5.14)
и фильтр с двумя интеграторами, обеспечивающий системе астатизм второго порядка:
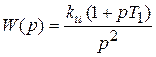 . (5.15)
. (5.15)
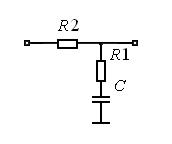
Рис. 5.5. Схема пропорционально-интегрирующего фильтра
( 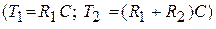
Таблица. 5.1
Значения коэффициенов ошибки
| V | 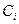
| Расчетные формулы |
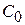
| 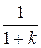
| |
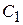
| 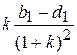
| |
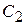
| 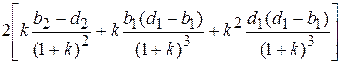
| |
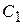
| ||
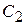
| 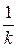
| |
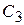
| 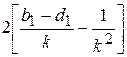
| |
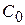
| ||
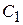
| ||
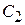
| 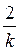
|
Это достаточно распространенный тип фильтра (на ВЧ – делитель, на НЧ – интегрирующая цепь); звено обеспечивает запаздывание по фазе.
Второй фильтр – соединенные последовательно форсирующее звено и два интегратора.
Пусть задающее воздействие определяется выражением
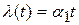 ,
,
а в качестве фильтра используем фильтр с передаточной функцией (5.14).
Величину установившейся ошибки определим по теореме о предельном значении оригинала
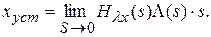
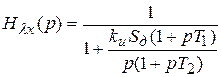 ;
;
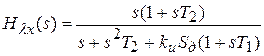 ; (5.16)
; (5.16)
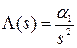 ─ изображение входного воздействия определяем по таблицам.
─ изображение входного воздействия определяем по таблицам.
Обозначим 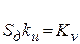 (добротность по скорости).
(добротность по скорости).
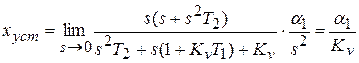 .
.
Таким образом, динамическая ошибка прямо пропорциональна скорости 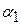 изменения задающего воздействия и обратно пропорциональна коэффициенту усиления разомкнутой системы.
изменения задающего воздействия и обратно пропорциональна коэффициенту усиления разомкнутой системы.
Для ФАПЧ 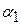 ─ значение расстройки номинальной частоты генератора и входного сигнала, следовательно,
─ значение расстройки номинальной частоты генератора и входного сигнала, следовательно,
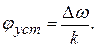 .
.
Для нахождения 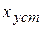 можно использовать и другие методы.
можно использовать и другие методы.
Известно, что
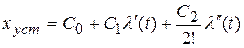 .
.
В системе с астатизмом первого порядка 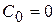 ;
; 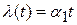 ;
; 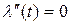 .
.
Следовательно,
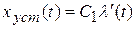 .
.
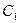 можно определить, используя передаточную функцию замкнутой системы
можно определить, используя передаточную функцию замкнутой системы 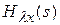 (5.16):
(5.16):
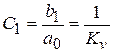 .
.
Следовательно, 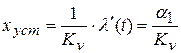
Используя передаточную функцию разомкнутой системы, 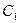 можно также определить по табл. 5.1.
можно также определить по табл. 5.1.
С фильтром (5.15) система является астатической с астатизмом 2-го порядка и при линейном воздействии 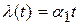 установившаяся ошибка равна нулю.
установившаяся ошибка равна нулю.
Пусть 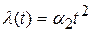 .
.
Определим величину установившейся ошибки, используя ее разложение по производным входного воздействия:
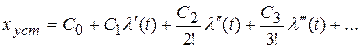 ;
;
Поскольку 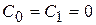 ;
; 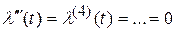 ,
,
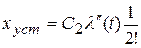 .
.
по табл. 4.1 определяем 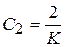 и вычисляем
и вычисляем 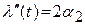
Таким образом,
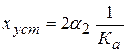 ,
,
где 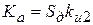 .
.
Дата добавления: 2020-10-25; просмотров: 811;











