Нелинейные системы радиоавтоматики
8.1. Методы исследования нелинейных систем
К нелинейным относят системы, описываемые нелинейными дифференциальными уравнениями.
Система является нелинейной вследствие наличия в ее составе звеньев, описываемых нелинейными дифференциальными уравнениями, или имеющих нелинейную статическую характеристику (например, дискриминационную).
Нелинейный режим работы имеет место в системе при выходе ошибки слежения за пределы линейного участка (переходной режим, срыв слежения, большой уровень помех и т.д.).
Методы анализа нелинейных систем:
Метод кусочно-линейной аппроксимации. Нелинейная характеристика разбивается на ряд линейных участков, в пределах каждого из которых система описывается линейным дифференциальным уравнением. Далее на каждом из этих участков система исследуется линейными методами; находятся решения, описывающие работу системы, которые затем «сшиваются». Метод удобен при небольшом числе участков разбиения. Недостаток метода в громоздкости вычислений при увеличении количества участков.
Метод гармонической линеаризации. Нелинейный элемент (НЭ) заменяется его линейным эквивалентом. Критерий эквивалентности состоит в равенстве первой гармоники напряжения на выходе НЭ и его линейного эквивалента по амплитуде и фазе при подаче на входы НЭ и его эквивалента гармонического сигнала. Метод эффективен, когда все высшие гармоники подавляются последующими цепями.
Метод фазовой плоскости. Применяется для исследования нелинейных систем, описываемых дифференциальными уравнениями первого и второго порядков. Состоит в построении и исследовании фазового портрета системы в координатах исследуемой величины и ее производной.
Используется для анализа переходных режимов работы, оценки устойчивости системы, возможности возникновения периодических колебаний
Моделирование на аналоговых и цифровых вычислительных машинах.Не имеет ограничений на количество и вид нелинейностей, порядок дифференциального уравнения, позволяет исследовать поведение системы при детерминированных и случайных воздействиях.
Отсутствие возможностей найти аналитические зависимости для исследуемых явлений является недостатком метода.
Метод статистической линеаризации. Состоит в замене НЭ его статистическим линейным эквивалентом. Используется для исследования нелинейных систем, описываемых дифференциальными уравнениями произвольного порядка. Метод является приближенным. Имеет место неоднозначность в решениях при использовании различных критериев эквивалентности замены.
Метод, основанный на использовании марковской теории случайных процессов позволяет исследовать системы, описываемые дифференциальными уравнениями первого и второго порядков, работающие в условиях действия случайных возмущений, и получить аналитические выражения для этих систем, что является его достоинством.
На практике используют комбинацию различных методов.
8.2.Анализ нелинейного режима работы системы ЧАП
Для определения некоторых характеристик системы, произведем качественный анализ системы ЧАП (рис. 8.1)
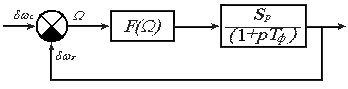
Рис. 8.1. Структурная схема нелинейной системы
Исходные данные:
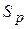 ─ крутизна регулировочной характеристики генератора;
─ крутизна регулировочной характеристики генератора;
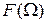 ─ дискриминационная характеристика;
─ дискриминационная характеристика;
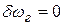 ─ нестабильность частоты генератора;
─ нестабильность частоты генератора;
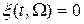 ─ флюктуационная составляющая;
─ флюктуационная составляющая;
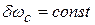 ─ отклонение от частоты от номинального значения..
─ отклонение от частоты от номинального значения..
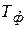 ─ постоянная времени фильтра.
─ постоянная времени фильтра.
Составим ДУ описывающее поведение системы:
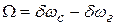 (8.1)
(8.1)
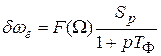 ; (8.2)
; (8.2)
Подставив (8.2) в (8.1), получим
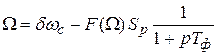 ;
;
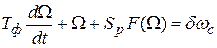 . (8.3)
. (8.3)
В установившемся режиме 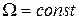 ;
; 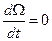 , следовательно,
, следовательно,
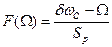 . (8.4);
. (8.4);
Решение уравнения (8.4) может быть найдено графическим способом (рис. 8.2).
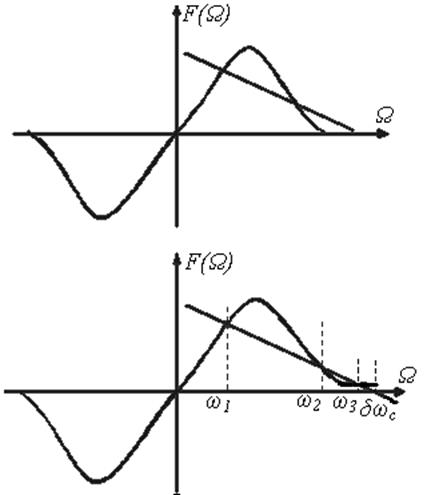
Рис.8.2
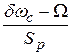 - прямая проходящая через точку
- прямая проходящая через точку 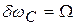 , с наклоном
, с наклоном 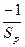 .
.
Абсциссы точек 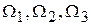 и есть решение этого ДУ.
и есть решение этого ДУ.
Исследуем на устойчивость в «малом» систему в точках 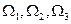 .
.
С этой целью линеаризируем дискриминационную характеристику в окрестности точек равновесия системы и представим ее зависимостью
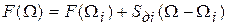 ; (8.5)
; (8.5)
где 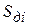 - крутизна дискриминационной характеристики;
- крутизна дискриминационной характеристики;
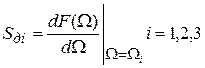 .
.
Подставим (8.5) в (8.3) и введем новую переменную 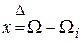 ; в результате получим дифференциальное уравнение следующего вида:
; в результате получим дифференциальное уравнение следующего вида:
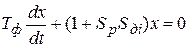 . (8.6)
. (8.6)
Уравнение (8.6) описывает поведение системы в окрестности точек равновесия системы. Определим исходя из алгебраического критерия условия устойчивости системы:
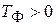 ;
; 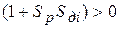 .
.
В точке, соответствующей решению 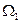 ,
, 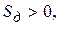 следовательно,
следовательно,
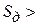
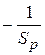
Таким образом 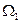 соответствует устойчивому состоянию равновесия.
соответствует устойчивому состоянию равновесия.
В точке, соответствующей 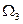 ,
, 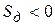 , но
, но 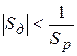 , поэтому
, поэтому 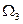 соответствует устойчивому состоянию равновесия.
соответствует устойчивому состоянию равновесия.
В точке, соответствующей 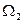 ,
, 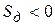 и
и 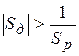 , здесь условие устойчивости не выполняется.
, здесь условие устойчивости не выполняется.
Если задать ряд значений начальной частотной расстройки, можно получить ряд решений, определяющих ошибку 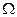 , и построить зависимость установившегося значения ошибки от величины начальной расстройки по частоте (рис. 8.3).
, и построить зависимость установившегося значения ошибки от величины начальной расстройки по частоте (рис. 8.3).
Для разомкнутой системы эта зависимость линейна.
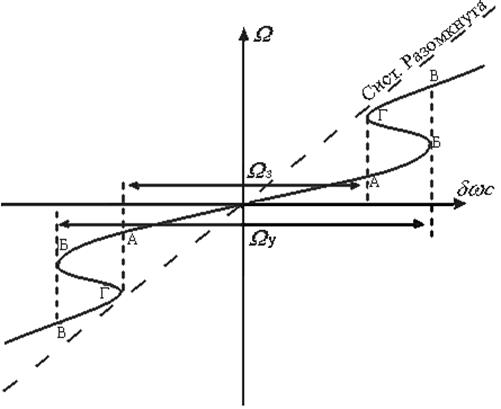
Рис. 8.3. Зависимость частотной ошибки от первоначальной частотной расстройки
Для замкнутой системы при увеличении 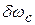 увеличивается и
увеличивается и 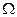 , и в точке Б система скачком переходит в точку В: происходит срыв слежения. При дальнейшем увеличении
, и в точке Б система скачком переходит в точку В: происходит срыв слежения. При дальнейшем увеличении 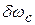 система будет вести себя как и разомкнутая. При уменьшении
система будет вести себя как и разомкнутая. При уменьшении 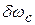 система войдет в режим синхронизма в точке Г, ошибка скачком уменьшится, при этом
система войдет в режим синхронизма в точке Г, ошибка скачком уменьшится, при этом 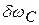 будет меньше, чем при срыве слежения.
будет меньше, чем при срыве слежения.
Диапазон первоначальных расстроек частот входного сигнала и генератора, в пределах которого сохраняется режим слежения называют полосой удержания. Диапазон первоначальных расстроек, в пределах которого система выведенная из синхронизма способна войти в режим синхронизма называют полосой захвата 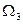 .
.
Участок В– Г соответствует решению типа 3 (устойчивому состоянию).
Участок Б – Г соответствует решению типа 2 (неустойчивому состоянию).
Участок Б – Б соответствует решению типа 1(устойчивому состоянию).
Аналогичную зависимость можно получить для системы ФАПЧ (рис. 8.4),
Где 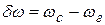 - расстройка между частотой входного сигнала и частотой собственных колебаний опорного генератора;
- расстройка между частотой входного сигнала и частотой собственных колебаний опорного генератора;
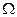 - ошибка слежения по частоте.
- ошибка слежения по частоте.
Не для всех систем 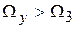 . Это определяется типом фильтра и дискриминатора. Для цифровых следящих систем
. Это определяется типом фильтра и дискриминатора. Для цифровых следящих систем 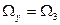 и называется полосой синхронизации.
и называется полосой синхронизации.
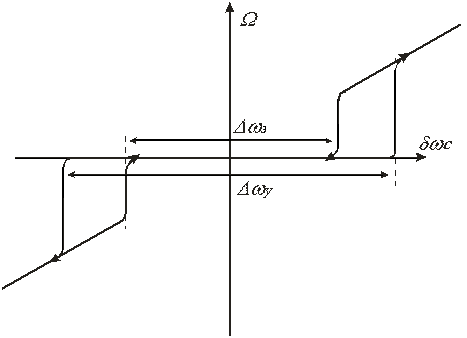
Рис. 8.4. Зависимость частотной ошибки от первоначальной частотной расстройки
8.3. Метод фазовой плоскости
Предположим, что поведение следящей системы описывается нелинейным дифференциальным уравнением второго порядка
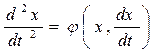 . (8.7)
. (8.7)
Обозначим
х = х1;
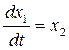 ;
;
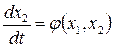 . (8.8)
. (8.8)
Состояние системы, описываемой уравнениями (8.8), определяется в каждый момент времени величинами 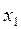 и
и 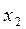 т.е. величиной координаты
т.е. величиной координаты 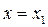 и скоростью ее изменения. Это состояние системы можно отобразить точкой на плоскости с координатами
и скоростью ее изменения. Это состояние системы можно отобразить точкой на плоскости с координатами 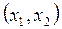 , называемой фазовой плоскостью. При изменении состояния системы изображающая точка перемещается на фазовой плоскости по кривым, которые называют фазовыми траекториями. Совокупность фазовых траекторий для различных начальных условий называют фазовым портретом.
, называемой фазовой плоскостью. При изменении состояния системы изображающая точка перемещается на фазовой плоскости по кривым, которые называют фазовыми траекториями. Совокупность фазовых траекторий для различных начальных условий называют фазовым портретом.
Чтобы получить уравнение фазовых траекторий, исключим из (2) время, поделив для этого второе из них на первое:
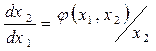 . (8.9)
. (8.9)
Его решение 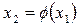 . Каждой комбинации начальных условий
. Каждой комбинации начальных условий 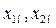 соответствует свое решение уравнения (3) и своя фазовая траектория.
соответствует свое решение уравнения (3) и своя фазовая траектория.
В качестве примера рассмотрим затухающий колебательный процесс, показанный на рис.8.5.
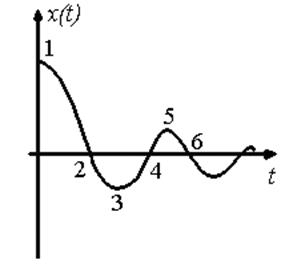
Рис.8.5. Затухающий колебательный процесс
Цифрами отметим характерные точки кривой и сопоставим их с фазовой траекторией. В точке 1 х 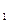 (0)
(0) 
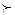 0, х
0, х 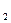 (0)=0, поэтому фазовая траектория начинается на положительной полуоси абсцисс (рис.8.6). В точке 2 х
(0)=0, поэтому фазовая траектория начинается на положительной полуоси абсцисс (рис.8.6). В точке 2 х 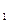 =0, х
=0, х 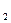
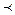 0, поэтому эта точка расположена на отрицательной полуоси абсцисс. В точке 3 х
0, поэтому эта точка расположена на отрицательной полуоси абсцисс. В точке 3 х 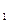
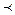 0, х
0, х 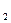 (0)=0, и на фазовой плоскости она расположена на отрицательной части горизонтальной оси и т.д. В результате для затухающего колебательного процесса фазовая траектория имеет вид сходящейся спирали.
(0)=0, и на фазовой плоскости она расположена на отрицательной части горизонтальной оси и т.д. В результате для затухающего колебательного процесса фазовая траектория имеет вид сходящейся спирали.
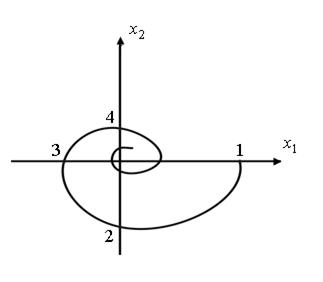

Рис.8.6. Фазовая траектория затухающего колебательного процесса
Для затухающего монотонного процесса (рис.8.7а) фазовая траектория приведена на рис.8.7б.
Eсли в системе возникают периодические колебания, на фазовой плоскости они отображаются в виде замкнутой кривой, называемой предельным циклом. Предельный цикл является устойчивым, если при некоторых отклонениях от него фазовая траектория вновь стремится к предельному циклу. При расхождении фазовых траекторий предельный цикл называется неустойчивым.
Построение фазовых траекторий позволяет судить о свойствах нелинейных систем по переходному процессу.
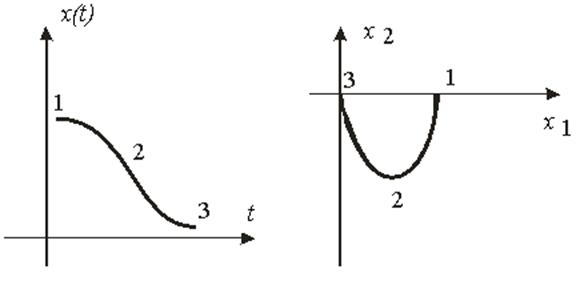
Рис.8.7. Апериодический процесс и его фазовая траектория
Построение фазового портрета системы обычно начинают с определения его характера вблизи точек равновесия системы, в которых производные 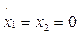 . Координаты точек равновесия
. Координаты точек равновесия 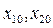 определяются, как
определяются, как
следует из (8.8), равенствами 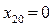 ,
, 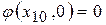 . Точки равновесия при построении фазового портрета системы называют особыми.
. Точки равновесия при построении фазового портрета системы называют особыми.
Поведение фазовых траекторий вблизи особых точек зависит от характера корней 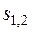 соответствующего характеристического уравнения
соответствующего характеристического уравнения
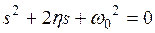 ,
,
где
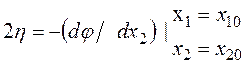 ,
, 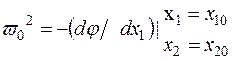 ;
;
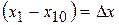 - отклонение от состояния равновесия.
- отклонение от состояния равновесия.
Если 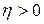 и
и 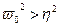 , то процесс
, то процесс 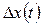 является затухающим гармоническим колебанием
является затухающим гармоническим колебанием
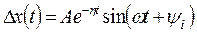 , (8.10)
, (8.10)
где 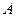 и
и 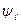 - амплитуда и начальная фаза колебания;
- амплитуда и начальная фаза колебания; 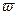 - его частота, равная
- его частота, равная
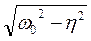 .
.
Продифференцировав выражение (8.10) для 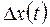 по времени, получим
по времени, получим
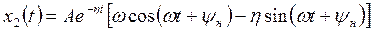 . (8.11)
. (8.11)
Фазовая траектория, построенная по приведённым выражениям для процессов 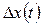 и
и 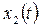 , имеет вид скручивающейся спирали (см. рис. 8.8), получившей название – устойчивый фокус.
, имеет вид скручивающейся спирали (см. рис. 8.8), получившей название – устойчивый фокус.
При 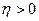 и
и 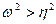 процесс
процесс 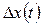 является гармоническим колебанием с нарастающей амплитудой. Особая точка соответствует при этом неустойчивому состоянию равновесия и называется неустойчивым фокусом (см. рис. 8.9).
является гармоническим колебанием с нарастающей амплитудой. Особая точка соответствует при этом неустойчивому состоянию равновесия и называется неустойчивым фокусом (см. рис. 8.9).
При выполнении условия 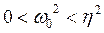 корни
корни 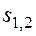 действительные и имеют одинаковый знак. Если они отрицательны, то особая точка является устойчивым узлом (см. рис. 8.10). Положительным корням
действительные и имеют одинаковый знак. Если они отрицательны, то особая точка является устойчивым узлом (см. рис. 8.10). Положительным корням 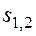 соответствует особая точка типа неустойчивого узла (см. рис.8.11 ). При
соответствует особая точка типа неустойчивого узла (см. рис.8.11 ). При 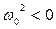 корни
корни 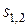 действительные и имеют разные знаки. Особая точка называется седлом (см. рис. 8. 12).
действительные и имеют разные знаки. Особая точка называется седлом (см. рис. 8. 12).
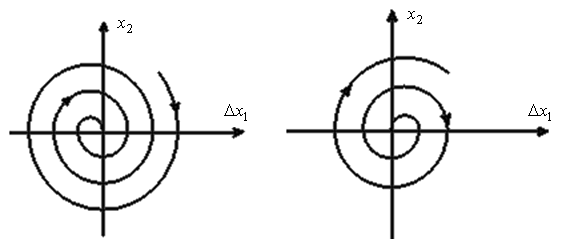
Рис.8.8. Устойчивый фокус Рис.8.9. Неустойчивый фокус
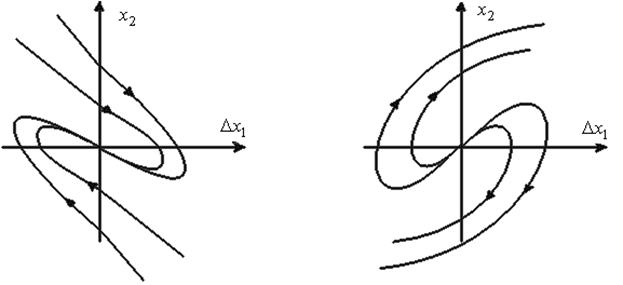
Рис.8.10. Устойчивый узел Рис.8.11. Неустойчивый
фокус
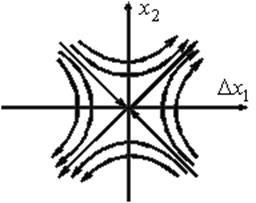
Рис.8.12. Особая точка типа седла
Для построения фазового портрета необходимо определить изоклины. Изоклиной называют геометрическое место точек в котором касательные к фазовым траекториям имеют постоянный наклон.
Уравнение изоклины:
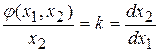 .
.
Для горизонтальных касательных уравнение изоклины:
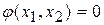 ;
;
для вертикальных:
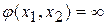 .
.
Ось абсцисс является изоклиной вертикальных касательных. Для особых точек типа узла и седла существуют изоклины, совпадающие с фазовыми траекториями: ( 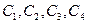 ). Они называются сепаратрисcами.
). Они называются сепаратрисcами.
Рассмотрим пример.
Определим условия вхождения в синхронизм системы, представленной структурной схемой (рис.8.13), если задающее воздействие изменяется по линейному закону 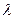 (t) = at и в момент включения системы при t = 0 начальная ошибка имеет конечное значение х(0) = х
(t) = at и в момент включения системы при t = 0 начальная ошибка имеет конечное значение х(0) = х 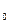 .
.


а)
б)
Рис.8.14. Дискриминационная характеристика (а) и фазовый портрет (б)
Обозначим ошибку слежения
х(t)= х 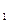 =
= 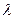 (t) – y(t).
(t) – y(t).
Тогда производная этой функции


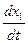 =
= 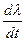 –
– 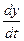 = a –
= a – 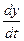 .
.
Так как в качестве фильтра системы используется интегрирующее звено, то
y(t) = k F(x 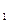 )/p.
)/p.
В результате уравнение ошибки примет вид
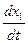 = а – k F(x
= а – k F(x 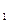 ).
).
Обозначим
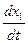 = х
= х 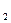
и, пользуясь уравнением
х 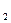 = а – k F(x
= а – k F(x 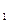 ),
),
построим фазовый портрет системы в координатах (x 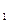 , х
, х 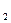 ) для различных значений скорости изменения задающего воздействия а.
) для различных значений скорости изменения задающего воздействия а.
При различных значениях а кривая х 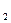 =f(x
=f(x 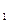 ) перемещается параллель-
) перемещается параллель-
но самой себе. На рис.8.14 изображено семейство кривых для положительной скорости а. Обозначим максимальное значение функции F(x) = F 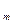 . Направление движения изображающей точки обозначим в соответствии с правилами: в верхней полуплоскости слева направо; в нижней – справа налево. Проанализируем фазовый портрет.
. Направление движения изображающей точки обозначим в соответствии с правилами: в верхней полуплоскости слева направо; в нижней – справа налево. Проанализируем фазовый портрет.
При а=0 ошибка слежения х 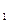
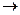 0 при начальных значениях | х
0 при начальных значениях | х 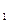 (0)|
(0)| 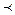
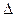 , что следует из направления движений на фазовой траектории. Если 0
, что следует из направления движений на фазовой траектории. Если 0 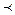 а
а 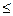 k F
k F 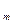 , то x
, то x 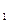 стремится к устойчивой точке 1, если начальное рассогласование х
стремится к устойчивой точке 1, если начальное рассогласование х 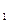 (0) меньше величины
(0) меньше величины 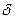 , соответствующей точке 2. Когда х
, соответствующей точке 2. Когда х 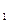 (0)
(0) 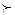
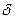 , захвата не происходит, так как x
, захвата не происходит, так как x 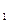 неограниченно растет. Если скорость /а/
неограниченно растет. Если скорость /а/ 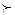 k F
k F 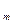 , то захвата не будет ни при каких начальных условиях, поскольку нет устойчивых точек на фазовой траектории. Таким образом, условия захвата сигнала, изменяющегося с постоянной скоростью а, состоят в выполнении неравенства kF
, то захвата не будет ни при каких начальных условиях, поскольку нет устойчивых точек на фазовой траектории. Таким образом, условия захвата сигнала, изменяющегося с постоянной скоростью а, состоят в выполнении неравенства kF 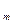
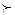 а. При этом область захвата х(0)
а. При этом область захвата х(0) 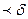 . Величина
. Величина 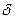 находится из уравнения а – kF(
находится из уравнения а – kF( 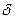 ) =0. Первый корень этого уравнения соответствует точке 1 устойчивого равновесия, а второй корень, соответствующий точке 2, является искомой величиной
) =0. Первый корень этого уравнения соответствует точке 1 устойчивого равновесия, а второй корень, соответствующий точке 2, является искомой величиной 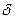 .
.
8.4. Метод статистической линеаризации
Метод основан на замене нелинейного преобразования процессов статистически эквивалентными им линейным преобразованиями. Нелинейный элемент заменяется линейным эквивалентом (рис. 8.15). В результате замены система линеаризуется, что позволяет использовать методы исследования линейных систем.
Замена нелинейного преобразования линейным является приближенной и справедливой лишь в некоторых отношениях. Поэтому не существует однозначной эквивалентности при использовании различных критериев.
В частности, если нелинейность определяется безынерционной зависимостью вида
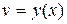 , (8.12)
, (8.12)
используется два критерия эквивалентности.
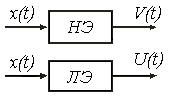
Рис. 8.15
Первый критерий предполагает равенство на выходе нелинейного элемента и его линейного эквивалента математических ожиданий и дисперсий процессов.
Второй критерий – минимум среднего квадрата разности процессов на выходе нелинейного элемента и его линейного эквивалента.
Процесс на входе и выходе нелинейного элемента представим в виде:
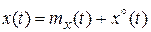 ; (8.13)
; (8.13)
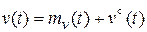 , (8.14)
, (8.14)
где 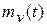 ─ математическое ожидание процесса на выходе НЭ;
─ математическое ожидание процесса на выходе НЭ;
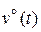 ─ центрированная случайная составляющая.
─ центрированная случайная составляющая.
Процесс на выходе линейного эквивалента представляется в следующем виде:
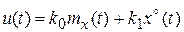 , (8.15)
, (8.15)
где 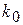 ─ коэффициент передачи линейного эквивалента по математическому ожиданию;
─ коэффициент передачи линейного эквивалента по математическому ожиданию; 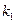 ─ коэффициент передачи по центрированной случайной составляющей.
─ коэффициент передачи по центрированной случайной составляющей.
Воспользуемся первым критерием эквивалентности:

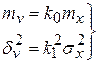 . (8.16)
. (8.16)
Из этих уравнений находим
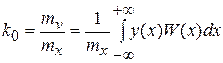 ;
;
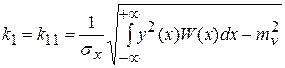 ,
,
где 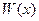 ─ плотность вероятности процесса на входе нелинейного элемента.
─ плотность вероятности процесса на входе нелинейного элемента.
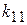 - коэффициент передачи линейного эквивалента по центрированной случайной составляющей (по первому критерию).
- коэффициент передачи линейного эквивалента по центрированной случайной составляющей (по первому критерию).
По второму критерию эквивалентности:
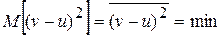 ;
;
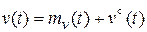 ;
;
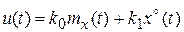 ;
;
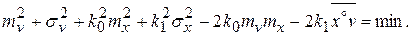 ;
;
Для определения 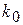 и
и 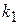 , при которых выполняется условие эквивалентности, найдем частные производные и приравняем их нулю:
, при которых выполняется условие эквивалентности, найдем частные производные и приравняем их нулю:
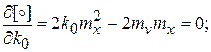
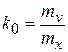 ;
;
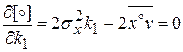 ;
; 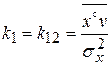 ;
; 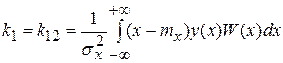 .
.
При расчете этих коэффициентов полагают, что распределение на входе нормальное:
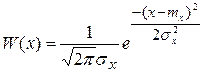 ;
;
Определив величины
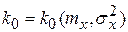 ;
; 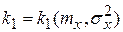 .
.
для типовых нелинейностей, заменяют последние коэффициентами передачи линейного эквивалента и анализируют систему линейными методами.
.
Для основных типов нелинейностей и нормальном распределении входного процесса коэффициенты рассчитаны и представлены в виде табличных значений. В частности, для характеристики релейного типа (рис.8.16)
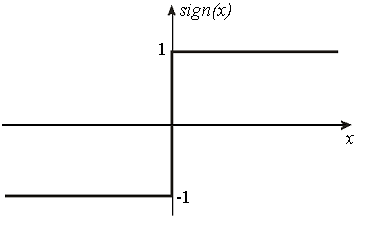
Рис.8.16. Характеристика релейного типа:
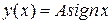 ;
; 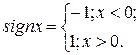
коэффициенты равны:
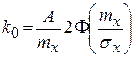 ;
; 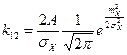 ;
; 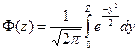 ;
;
8.5. Метод гармонической линеаризации
8.5.1. Основы метода
Метод используется для исследования нелинейных систем, описываемых дифференциальными уравнениями различного порядка. Эффективен для расчета параметров собственных колебаний в системе, используется также для анализа точности при гармоническом задающем воздействии.
Рассмотрим метод применительно к расчету параметров собственных колебаний в нелинейной системе.
Разделим систему на линейную часть и нелинейное звено (рис.8.17).
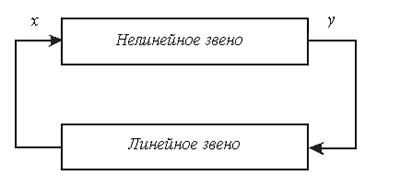
Рис.8.17. Модель нелинейной системы
Уравнение линейной части:
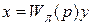 , (8.17)
, (8.17)
При возникновении автоколебаний процесс 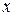 на выходе линейной части не является строго гармоническим, но мы будем полагать, что линейное звено является фильтром нижних частот и подавляет все гармоники, за исключением первой. Это предположение называется гипотезой фильтра. Если она не подтверждается, то ошибки при применении гармонической линеаризации могут быть значительными.
на выходе линейной части не является строго гармоническим, но мы будем полагать, что линейное звено является фильтром нижних частот и подавляет все гармоники, за исключением первой. Это предположение называется гипотезой фильтра. Если она не подтверждается, то ошибки при применении гармонической линеаризации могут быть значительными.
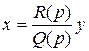 .
.
Пусть
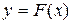 ;
; 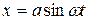 . (8.18)
. (8.18)
Представим 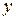 в виде ряда Фурье:
в виде ряда Фурье:
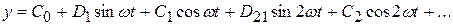 ;(8.19)
;(8.19)
Полагаем, что
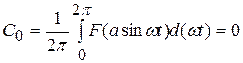 .
.
Это справедливо, если 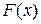 симметрична относительно начала координат и отсутствует внешнее воздействие. Полагая, что высшие гармоники подавляются, будем искать только
симметрична относительно начала координат и отсутствует внешнее воздействие. Полагая, что высшие гармоники подавляются, будем искать только 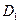 и
и 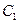
Из уравнения (8.18) находим:
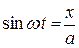 ;
; 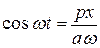 . (8.20)
. (8.20)
Подставив (8.20) в (8.19) и ограничив ряд слагаемыми первой гармоники, получим:
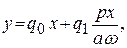 (8.21)
(8.21)
где

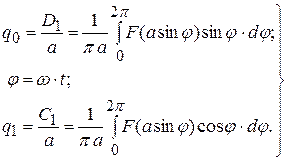 (8.22)
(8.22)
Таким образом, нелинейное уравнение для 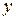 заменили приближенным линейным уравнением (8.21) для первой гармоники.
заменили приближенным линейным уравнением (8.21) для первой гармоники.
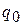 и
и 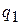 называют гармоническими коэффициентами передачи нелинейного звена. Коэффициенты
называют гармоническими коэффициентами передачи нелинейного звена. Коэффициенты 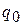 и
и 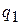 в рассматриваемом случае зависят от амплитуды, при более сложной нелинейной зависимости зависят еще и от частоты.
в рассматриваемом случае зависят от амплитуды, при более сложной нелинейной зависимости зависят еще и от частоты.
Рассчитанные значения коэффициентов гармонической линеаризации для типовых нелинейностей можно найти в учебниках и справочной литературе.
Передаточная функция разомкнутой системы может быть представлена в следующем виде:
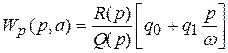 ;
; 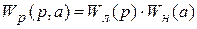 ;
;
где 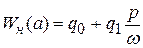 ─ эквивалентная передаточная функция нелинейно- го звена.
─ эквивалентная передаточная функция нелинейно- го звена.
Частотная передаточная функция разомкнутой системы
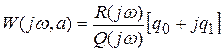 .
.
Характеристическое уравнение
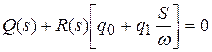 .
.
Модуль частотной передаточной функции нелинейного звена
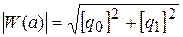 .
.
Фазочастотная характеристика
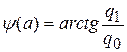 ; (
; ( 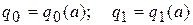 )
)
Модуль определяет отношение амплитуд, а 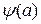 фазовый сдвиг на выходе относительно входного сигнала.
фазовый сдвиг на выходе относительно входного сигнала.
Если 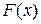 симметрична относительно начала координат, однозначна и не имеет гистерезиса, то
симметрична относительно начала координат, однозначна и не имеет гистерезиса, то 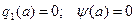 и тогда
и тогда
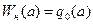 .
.
Часто при анализе используется величина обратная 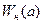 . Она называется гармоническим импедансом нелинейного звена:
. Она называется гармоническим импедансом нелинейного звена:
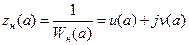 .
.
8.5.2. Расчет автоколебаний по критерию Найквиста
В соответствии с критерием Найквиста строится годограф частотной передаточной функции разомкнутой системы
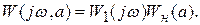
Условием возникновения в системе колебаний является прохождение амплитудно-фазовой характеристики через точку (-1,j0) комплексной плоскости. Для определения условий прохождения годографа через эту точку приравняем
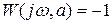 .
.
Чтобы решить это уравнение можно, задавая значение амплитуды, строить амплитудно-фазовую характеристику(рис. 8.18)Значение амплитуды а=А, при которой АФХ пройдет через точку (-1,j0) будет соответствовать амплитуде собственных колебаний. Значение частоты определяют по частоте в точке (-1,j0).
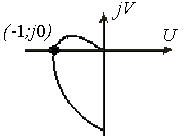
Рис. 8.18. Амплитудно-фазовая характеристика нелинейной системы
Тогда искомое колебание
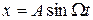 .
.
При нелинейной зависимости вида 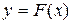 передаточную функцию разомкнутой системы можно представить в виде
передаточную функцию разомкнутой системы можно представить в виде
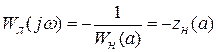 . (8.23)
. (8.23)

Рис.8.19. Графический метод решения уравнения (8.23)
Это уравнение решается графическим методом (рис.8.19).
Строим амплитудно-фазовую характеристику линейного звена и кривую импеданса нелинейного звена. Определяем точку пересечения. Частоту 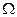 определим по АФХ линейного звена в точке пересечения. Амплитуду А определим по кривой импеданса нелинейного звена.
определим по АФХ линейного звена в точке пересечения. Амплитуду А определим по кривой импеданса нелинейного звена.
Чтобы определить являются ли колебания устойчивыми автоколебаниями, нужно задать приращение амплитуды 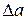 ; при этом точка на импедансе смещается влево вниз. Это будет соответствовать уменьшению
; при этом точка на импедансе смещается влево вниз. Это будет соответствовать уменьшению 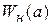 , следовательно, кривая годографа ПФ разомкнутой системы не будет охватывать точку с координатами
, следовательно, кривая годографа ПФ разомкнутой системы не будет охватывать точку с координатами 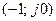 . Поэтому амплитуда колебаний начнет уменьшаться, и система вернется в исходное состояние. То же будет и при отрицательном приращении.
. Поэтому амплитуда колебаний начнет уменьшаться, и система вернется в исходное состояние. То же будет и при отрицательном приращении.
Критерий устойчивости периодического режима сводится к тому, чтобы часть кривой 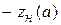 соответствующая меньшим амплитудам, охватывалась амплитудно-фазовой характеристикой линейной части.
соответствующая меньшим амплитудам, охватывалась амплитудно-фазовой характеристикой линейной части.
При отсутствии в системе периодических режимов (решения уравнения (8.23)) можно предположить, что система будет устойчива.
Условие устойчивости равновесного состояния (отсутствия автоколебаний): при устойчивой или нейтральной в разомкнутом состоянии линейной части её АФХ не охватывает годограф 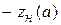 .
.
Дата добавления: 2020-10-25; просмотров: 666;











