Устойчивость радиоэлектронных следящих систем

4.1 Понятие устойчивости

Устойчивость - способность системы возвращаться в состояние равновесия после прекращения возмущающего воздействия, которым система была выведена из состояния равновесия.

Устойчивость является одним из основных показателей качества следящих систем. Система, не обладающая устойчивостью, практически неработоспособна. Устойчивость определяется характером собственных колебаний в системе при отсутствии внешних воздействий.

Дифференциальное уравнение, описывающее работу следящей системы:

, (4.1)

где 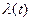- задающее воздействие; y(t) – управляемая величина.

Решение дифференциального уравнения представляется суммой общего решения однородного дифференциального уравнения и частного решения неоднородного дифференциального уравнения:

,

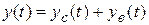где 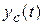- общее решение однородного дифференциального уравнения, определяющее характер собственных колебаний в системе при отсутствии внешних воздействий; 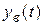- частное решение неоднородного дифференциального уравнения, определяющее реакцию системы на внешнее воздействие.

Таким образом, характер собственных колебаний определяется решением уравнения, которое имеет вид:

,

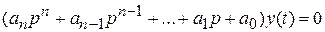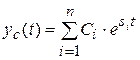, (4.2)

где 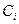- коэффициенты, определяемые начальными условиями ( начальные условия – значения выходной величины и её n-1 производных при t=0 ); 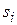- корни характеристического уравнения, получаемого из знаменателя передаточной функции:

.

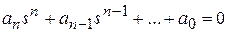Если все вещественные корни характеристического уравнения отрицательные, а комплексные корни имеют отрицательные вещественные части, то, как следует из (3.2), собственные колебания системы являются затухающими и система является устойчивой.

Таким образом, для оценки устойчивости системы следует решить характеристическое уравнение и определить положение его корней на комплексной плоскости. Если все корни принадлежат левой полуплоскости комплексной плоскости – система устойчива. Если хотя бы один из корней находится в правой полуплоскости – система неустойчива. Однако вследствие сложности выражений для корней характеристических уравнений высоких порядков этот метод практически непригоден для анализа устойчивости. В связи с этим разработаны критерии устойчивости, позволяющие оценить устойчивость без решения характеристического уравнения. Существуют алгебраические и частотные критерии устойчивости.

4.2.Алгебраические критерии устойчивости

Алгебраически критерии устойчивости состоят в проверке системы неравенств, составленных из коэффициентов характеристического уравнения.

Для систем, описываемых дифференциальными уравнениями не выше 2-го порядка, необходимым и достаточным условием устойчивости является положительность коэффициентов характеристического уравнения:

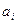>0; ; ,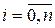

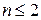где n ─ порядок характеристического уравнения.

Для n > 2 это условие является необходимым, но не достаточным. В этом случае из коэффициентов характеристического уравнения необходимо составить матрицу Гурвица, из матрицы составить определители и вычислить.

Если все n определителей, составленных из матрицы Гурвица. положительны при положительном значении коэффициента 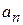, система устойчива.

Если хотя бы один из определителей отрицательный – система не устойчива. Система находится на границе устойчивости, если n-й определитель равен нулю.

Достоинством метода является его простота, недостатком – необходимость всякий раз при изменении параметров системы составлять матрицу и вычислять определители. Метод не позволяет также определить запасы устойчивости.

Рассмотрим пример. Пусть n=5.

Матрица составляется по следующему правилу.

По главной диагонали записывают коэффициенты от 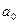до 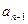. Затем заполняются строки

коэффициентами в порядке возрастания индексов слева направо от элемента, стоящего на главной диагонали и в порядке убывания индексов справа налево от элемента, стоящего на главной диагонали. Если индекс больше n или меньше нуля, то на соответствующей позиции записывают нуль.

После составления матрицы вычисляют определители Гурвица, симметричные относительно главной диагонали. Фактически необходимо вычислить n-2 определителя:

; ;

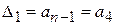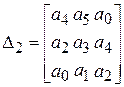и т.д. ( , .

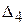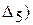При этом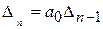

Если 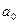> 0 то определяется .

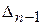4.3.Частотные критерии устойчивости

К частотным критериям ним относятся критерии Михайлова и Найквиста.

Критерий Михайлова базируется на исследовании характеристического комплекса замкнутой системы - знаменателя частотной передаточной функции замкнутой системы.

Как всякая комплексная функция, характеристический комплекс может быть представлен вектором на комплексной плоскости. При изменении частоты конец вектора описывает кривую, называемую годографом характеристического комплекса.

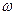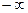При изменении от до 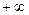аргумент характеристического комплекса приобретает приращение, величина которого определяется порядком характеристического комплекса и устойчивостью системы.

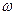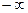Если при изменении от до 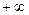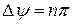,то система является устойчивой. Если 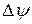< то система неустойчива.

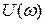- содержит четные степени. При изменении 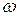от 0 до 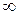система будет устойчива, если и не устойчива, если .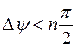

Применительно к поведению годографа характеристического комплекса критерий может быть сформулирован следующим образом: замкнутая система устойчива, если при изменении частоты 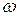от 0 до 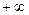годограф характеристического комплекса последовательно прочерчивает n – квадрантов. Если последовательность нарушается, система неустойчива. Если годограф проходит через начало координат, система находится на границе устойчивости (рис. 4.1).

Практическое применение критерия на обязательно требует построения годографа.

Пример.

Пусть порядок характеристического комплекса n=6. Разделим характеристический комплекс на действительную и мнимую части, действительная содержит коэффициенты с четными индексами, а мнимая – с нечетными:

;

.

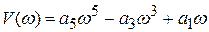Рис. 4.1. Годографы характеристического комплекса

Находим корни мнимой части характеристического комплекса, приравнивая его нулю: Im( 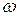) = 0. Найденные значения корней подставим в действительную часть и вычислим ее. Если действительная часть меняет знак при последовательной подстановке корней в порядке увеличения их значений, то система устойчива. Иначе говоря, в устойчивой системе корни мнимой и действительной частей характеристического комплекса перемежаются.

Поскольку в замкнутой системе все передаточные функции, связывающие входные и выходные величины, не отличаются знаменателем, то для определения устойчивости можно использовать характеристический комплекс любой частотной передаточной функции замкнутой системы.

Коэффициент ( 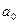) является коэффициентом усиления разомкнутой системы 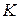, при увеличении 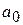годограф смещается вправо и при критическом значении 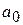пройдет через начало координат. Поэтому величина А (рис. 4.1) определяет запас устойчивости по амплитуде.

Критерий Найквиста базируется на исследовании поведения годографа частотной передаточной функции (амплитудно-фазовой характеристики) разомкнутой системы.

Рис.4.2. Годографы частотной передаточной функции

разомкнутой системы

Если годограф частотной передаточной функции разомкнутой системы, устойчивой в разомкнутом состоянии, при изменении частоты 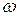от 0 до 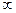не охватывает точку с координатами (-1;j0), то система устойчива, в противном случае система не устойчива (рис. 4.2).

Если годограф проходит через точку с координатами (-1;j0), то система находится на границе устойчивости. Это означает, что на некоторой частоте фазовый сдвиг равен 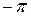,а модуль частотной передаточной функции А(ω)=1. Поскольку в замкнутой системе имеет место отрицательная обратная связь, то при таком фазовом сдвиге обратная связь становится положительной и выполняются условия самовозбуждения.

Для систем, содержащих интегрирующие звенья, годограф уходит в «бесконечность» при 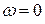. Тогда, чтобы решить охватывает или нет годограф точку с координатами (-1;j0),его дополняют дугой бесконечно большого радиуса, которая начинается на положительной полуоси вещественных чисел и заканчивается на пересечении с годографом. Дуга проводится в направлении по часовой стрелке.

Необходимость в дополнении годографа дугой обусловлена следующим. Вывод критерия Найквиста базируется на критерии устойчивости Михайлова, из которого следует: если в точку с координатами (-1;j0),поместить начало вектора, соединяющего эту точку с кривой АФХ разомкнутой системы (рис.4.3), то для устойчивой системы этот вектор при изменении частоты 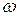от 0 до 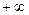, описав АФХ этой системы, не должен совершить ни одного оборота вокруг точки с координатами (-1;j0). Если же АФХ охватывает эту точку, то полное приращение аргумента вектора составит 360 градусов.

Критерий позволяет оценить запас устойчивости по фазе и амплитуде (рис. 4.4). Запас устойчивости по фазе показывает на какую величину необходимо увеличить запаздывание в системе, чтобы она оказалась на границе устойчивости и рассчитывается по формуле:

,

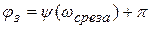где 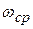─ частота среза определяемая из условия: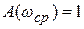

Рис.4.3.Годограф, дополненный дугой

Запас устойчивости по фазе для хорошо демпфированных систем должен составлять .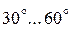

Запас устойчивости по амплитуде В показывает во сколько раз необходимо увеличить усиление в системе, чтобы она оказалась на границе устойчивости:

,

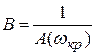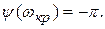
Рис 4.4. Определение запасов устойчивости

4.4.Определение устойчивости с помощью ЛАЧХ разомкнутой системы

Устойчивость минимально-фазовых систем, может быть определена по ЛАЧХ. Необходимым и достаточным условием устойчивости в этом случае является пересечение ЛАЧХ оси частот с наклоном -20дБ/дек.). Запас считается достаточным, если протяженность этого участка не менее одной декады.

Если система не является минимально-фазовой, то для определения устойчивости и запаса устойчивости, необходимо использовать ЛФЧХ.

Условие устойчивости: значение фазы на частоте среза меньше :

.

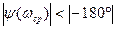Запас устойчивости по фазе:

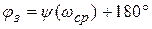или .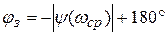

Запас устойчивости по амплитуде определяется на : ;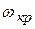

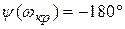Запас устойчивости по амплитуде 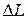показывает на сколько дБ необходимо увеличить усиление в системе, чтобы она оказалась на границе устойчивости (рис. 4.5)

Рис.4.5. Логарифмические характеристики разомкнутых систем: 1 – ЛЧХ устойчивой системы; 2 – ЛЧХ неустойчивой системы.

4.5. Абсолютно и условно устойчивые системы

Проанализируем АФХ разомкнутой системы (рис. 4.6), содержащей в своем составе апериодические и интегрирующие звенья. АФХ соответствует передаточной функции:

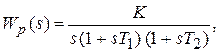
где К – коэффициент усиления или добротность системы.

Система устойчива, так как годограф не охватывает точку c координатами (-1, j0). С увеличением К запас устойчивости уменьшается и при некотором

Рис. 4.6. Годографы передаточной функции абсолютно устойчивых систем

значении коэффициента усиления 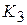( 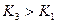на графике, рис.4.6) система теряет устойчивость.

Системы, добротность которых ограничена условиями устойчивости лишь сверху, называются абсолютно устойчивыми: .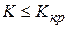

Как правило, величину коэффициента усиления выбирают из условия обеспечения заданной точности, а для достижения устойчивости вводят корректирующие звенья. В результате годограф деформируется (рис. 4.7).

Рис. 4.7. Годограф частотной передаточной функции разомкнутой системы с корректирующими звеньями

При этом .

Если для такой системы увеличивать К, то при некотором его значении система станет не устойчива (рис. 4.8).

При этом .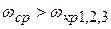

Рис.4.8. Годограф частотной передаточной функции

неустойчивой системы

Если К уменьшать, то годограф сжимается к оси ординат и система также становится неустойчивой (рис. 4.9). При этом

; .

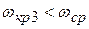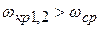Системы, добротность которых ограничена условием устойчивости как снизу, так и сверху называют условно устойчивыми. Для условно устойчивых систем число критических частот, меньших чем 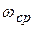, четно.

Рис.4.9. Годограф неустойчивой системы

Рассмотрим логарифмические характеристики систем такого типа (рис.4.10).

При увеличении К ЛАХ поднимается вверх, при этом каждая из асимптот перемещается вертикально; критические частоты не изменяются, а частота среза увеличивается. В результате все три значения критических частот оказываются меньше частоты среза и система становится не устойчивой. При уменьшении коэффициента усиления частота среза уменьшается, при этом одно значение критической частоты ( 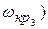становится меньше частоты среза и система станет также не устойчивой.

Рис. 4.10. Логарифмические характеристики условно устойчивой системы