Функции выпуска продукции; функции затрат ресурсов.
Функции зависимости издержек и дохода от объема производства.
Рассмотрим функции издержек C(q) и дохода фирмы R(q) = qp(q) в зависимости от объема производства q. Поведение функции дохода определяется функцией спроса p(q), рассмотренной выше. Поэтому рассмотрим более подробно поведение функции издержек. В типичном случае издержки фирмы велики при небольшом объеме производства q и вначале растут быстрее, чем доход. С увеличением объема производства скорость роста издержек уменьшается, и в какой-то момент они сравниваются с доходом, и фирма начинает получать прибыль. При увеличении объема производства прибыль увеличивается, достигая максимума при оптимальном значении q. При дальнейшем увеличении объема производства издержки снова начинают расти быстрее дохода (исчерпаны эффективные ресурсы, нужны дополнительные помещения, сырье, квалифицированная рабочая сила) и прибыль фирмы уменьшается, достигая отрицательных значений при достаточно больших объемах производства. Им, например, могут соответствовать функции R(q) = aq – bq2, C(q)=cq – dq2 + eq3 . Постройте графики функций дохода, издержек и прибыли.
Распределение налогового бремени.
Пусть р – цена товара на некотором рынке, S(p) – его предложение при цене р, D(p) – спрос. Равновесная цена р0 определяется уравнением S(р0)=D(р0).
Предположим, что вводится дополнительный налог с производителей в размере t с каждой единицы товара. Так как зависимость предложения от цены определяется прибылью, то St(p) = S(p – t), где St(p) – функция предложения после введения налога. Таким образом, кривая предложения после введения налога сдвигается на t вверх (рис. 1.1.5).
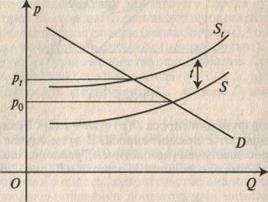 Рис. 1.1.5
Рис. 1.1.5
Пусть рt – новая равновесная цена. Равенство спроса и предложения при цене рt выражается уравнением
S(рt – t)=D(рt).
Так как S(p0) = D(p0), то из последнего равенства следует
S'(p0) (Dp – t)=D'(p0)Dp.
Итак, после введения дополнительного налога на покупку единицы товара затраты потребителя увеличатся на величину Dр, которую можно (приближенно) рассчитать по формуле
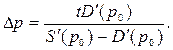
Соответственно, доход производителя (также на единицу продукции) уменьшится на
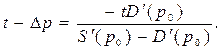
Следовательно, налоговое бремя распределяется между потребителями и производителями продукции в отношении
Dp:[t–Dp]=S'(p0):[ –D'(p0)],
а поскольку в точке р0 спрос равен предложению, то
S'(p0):[ –D'(p0)]= ЕS:[ – ЕD],
где ЕS, ЕD – коэффициенты эластичности спроса и предложения.
Пример1.1.6. Пусть ценовая эластичность спроса равна (–3), ценовая эластичность предложения равна 2, а вводимый налог t = 100. Тогда цена после введения этого налога увеличится на 2/(2+3)•100 = 40, а прибыль производителя от единицы продукции уменьшится на 100 – 40 = 60.
Цена, предельные издержки и объем производства.
Пусть q – выпуск продукции (в натуральных единицах); R(q) – выручка от продаж; C(q) – издержки производства, связанные с выпуском q единиц продукции. Тогда прибыль
П(q)=R(q) – C(q).
Предельной выручкой называется выручка от единицы продукции, предельными издержками – издержки от производства единицы продукции. Эти экономические понятия соответствуют значениям производных R'(q) и C'(q).
Предположим, что максимум прибыли достигается в некоторой точке q*¹0.
Тогда П'(q*) = 0, и в точке q = q* получаем равенство
R'(q*)=C'(q*). (1.1.11)
В экономической теории это равенство вводится как правило, согласно которому фирма, максимизирующая свою прибыль, устанавливает объем производства таким образом, чтобы предельная выручка была равна предельным издержкам.
В случае, когда объем производства q не влияет на цену продукции p, имеем R(q) =pq, R'(q) =p. Равенство (1.1.11) принимает вид
р=C'(q*). (1.1.12)
(для максимизации прибыли необходимо устанавливать такой объем производства, при котором цена была бы равна предельным издержкам).
Пример 1.1.7. Найти оптимальный объем производства, если р=15, C(q)=q3+3q.
Решение. Прибыль при производстве q единиц продукт будет
П(q) = l5q – q3– 3q =q(l2 – q2).
Используя равенство (1.2.2), получим
l5=C'(q*)=3(q*)2+3, откуда q*= 2.
Рассмотрим теперь более общий случай, когда цена продукции является функцией p=p(q) от объема выпуска q.
Из (1.1.11) получим уравнение для цены
R'(q*)=p'(q*)q*+ p(q*)= p(q*)(Epq(q*)+1)= C'(q*), откуда
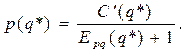 (1.1.13)
(1.1.13)
Так как Epq(q) < 0, то из равенства (1.1.13) следует, что цена р(q*) больше предельных издержек C '(q*).
Предположим теперь, что фирма является монополией. В этом случае при цене р фирма будет производить столько единиц продукции, сколько требуется покупателям, т.е. q = D(p), где D(p) – функция спроса. Таким образом, функция D(p) будет обратной функцией для функции p(q). Из свойств эластичности следует что Epq (q*)= 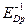 (p(q*)).
(p(q*)).
Пусть p*=p(q*) цена, соответствующая выпуску q*. Тогда уравнение (1.1.13) приобретает вид
 (1.1.14)
(1.1.14)
Пусть, например, ED = –1.2. Тогда ( 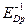 +1)–1=(–5/6+1)–1=6, т.е. цена монополиста р* в 6 раз (!) выше его предельных издержек.
+1)–1=(–5/6+1)–1=6, т.е. цена монополиста р* в 6 раз (!) выше его предельных издержек.
При неэластичном спросе монополия, стремящаяся увеличить свою прибыль, будет снижать объем выпуска. При этом издержки будут снижаться, а цена и прибыль – увеличиваться. В некоторый момент начнется массовый отказ (из-за отсутствия средств) потребителей от продукции данной монополии. Спрос снова станет эластичным.
Пример 1.1.8. Пусть C(q)=0.5q2 – издержки фирмы-монополиста, D(p) = 40 – 2p – функция спроса. Найдем зависимость цены р от количества произведенной продукции q. Так как q=D(p) = 40 – 2p, то p=20 – 0.5q. Итак, для функции D(p) мы нашли обратную функцию p(q). Прибыль имеет вид
П(q)=(20 – 0.5q)q – 0.5q2=20q – q2.
В точке q* максимума прибыли выполняется равенство П'(q*)=20 – 2q*=0. Находим оптимальный (для монополии) объем производства q*=10. Соответствующая цена будет р* = p(q*)=20 – 0.5q* =15. При этом предельные издержки С'(q*)= 10. Таким образом, цена, наиболее выгодная дли монополии, в полтора раза выше ее предельных издержек. Этот же результат можно получить и по формуле (1.1.14). Проверьте самостоятельно.
1.1.6. Экономические примеры производственной деятельности фирм.
Пусть z – количество продукции, выпущенной некоторой фирмой; х, у – затраты ресурсов двух видов; z=Q(x,у) – дифференцируемая функция, устанавливающая связь х, у и z. Предположим, что величины х, у, z заданы в натуральных единицах, и рx, рy, рz – соответствующие этим единицам постоянные цены. Тогда выручка (валовой доход) будет R(x, у) =рzQ(x, у), а функция прибыли запишется следующим образом:
p(x,y)= R(x, у) – рx x – рy y. (1.1.15)
Пусть z* – оптимальный (с точки зрения прибыли) выпуск продукции; х*, у* – соответствующие этому оптимальному количеству затраты ресурсов. Тогда точка М(х*,у*) является точкой локального максимума функции p(х, у). Согласно необходимому признаку локального экстремума, в точке М обращаются в нуль частные производные первого порядка:
p¢x(М)= R¢x(М) – рx = 0, p¢у(М) = R¢у(М) – ру = 0,
или R¢x(М) = рx, R¢x(М) = рx.
Вывод: в точке локального максимума прибыли предельная выручка от каждого ресурса совпадает с его ценой. Этот вывод сохраняется и в более общем случае, когда цена рz зависит от объема выручки: рz=рz(Q).
Рассмотрим теперь фирму-монополию, которая продает свою продукцию на двух независимых рынках. Пусть рi, qi – соответственно цена и количество продукции, проданной монополией на i-м рынке (i =1, 2). Из независимости рынков вытекает, что цена р1 не зависит от q2, т.е. р1 = р1(q1). Аналогично р2=p2(q2). Пусть С(q) – дифференцируемая функция издержек. Тогда функция прибыли имеет вид: p= р1q1 + р2q2 –С(q1+ q2).
В точке локального максимума прибыли имеем
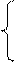
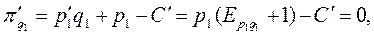
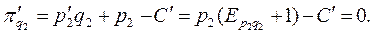
Отсюда получаем отношения цен:
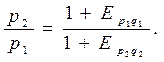 (1.1.16)
(1.1.16)
Так как рынки по предложению независимы, то, используя свойства эластичности функции одной переменной, имеем 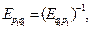
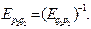
Пример1.1.9. На сколько процентов цена на втором из двух независимых рынков выше, если эластичность спроса на первом рынке (–2), а на втором – (–1,5)?
Решение. Используя формулу (1.1.16), находим 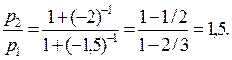
Следовательно,на втором рынке цена на 50% больше.
Практический блок
Пример 1.Пусть в результате корреляционно-регрессионного анализа (см. дисциплину «Эконометрика») получены следующие зависимости себестоимости продукции (у) от определяющих факторов (табл. 1.1.1.):
Таблица 1.1.1.
| Объем производства (х1) | у(х1)=0,62+58,74∙(1/х1) (гипербола) |  2,64 2,64
|
| Трудоемкость единицы продукции (х2) | у(х2)=9,3+9,83∙х2 (линейная функция) | 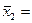 1,38 1,38
|
| Оптовая цена за 1т. энергоносителя (х3) | у(х3)=11,75+х31,6281 (степенная функция) | 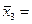 1,503 1,503
|
| Доля прибыли, изымаемая государством (х4) | у(х4)=14,87∙1,016х4 (показательная функция) | 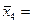 26,3 26,3
|
Тогда получаем:
a) для гиперболы у=b+a/x
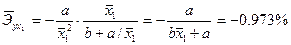
b) для линейной функции у=b+ax
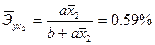
c) для степенной функции у=bxа

d) для показательной функции у=bах
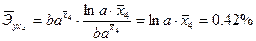
Из примера видно, что в наибольшей степени себестоимость зависит от оптовой цены за 1т. энергоносителя (1.63), затем от объемов производства (-0.973, т.е. с ростом объемов производства на 1% себестоимость падает почти на 1%).
Пример 2. При заданном бюджете М и ценах факторов производства rL и rK фирма работает по технологии, отображаемой функцией Q = LαKβ.
1. При каких объемах труда и капитала объем выпуска фирмы будет максимальным?
2. Как изменится капиталовооруженность труда, если:
а – бюджет фирмы возрастет в 1,5 раза;
б – цена труда возрастет в 1,5 раза?
Решение.
1. Из условия равновесия фирмы следует, что
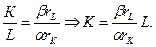
В соответствии с бюджетным ограничением
М= rLL+ rKK=rLL+ rK 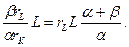
Отсюда максимальныe объемы труда и капитала будут:
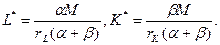
2а. Из условия равновесия фирмы следует, что капиталовооруженность труда не зависит от бюджета фирмы.
2б. Капиталовооруженность труда возрастет в 1,5 раза.
Пример 3. Продукция производится по технологии, отображаемой функцией Q = L0,25 K0,5. Цены факторов производства равны: rL = 1; rK = 3.
Определить минимум средних затрат в коротком периоде при использовании следующих объемов капитала: K = 10; 15; 20. Построить функции АС для каждого из указанных объемов капитала.
Решение.
При заданной технологии L =Q4/K2. Поэтому суммарные издержки TC=1∙Q4/K2 +3K, откуда следует, что средние затраты будут равны
AC= Q3/K2 +3K/Q.
Минимум АС определяется из условия
AC'= 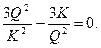
При K=10 АСmin =7,11; при K=15 АСmin=7,87; при K = 20 АСmin = 8,46.
Функции АС для каждого из указанных объемов капитала определяются по формулам:
АС10 = Q3/100 +3K/10, АС15 = Q3/225 +K/5, АС20 = Q3/400 +3K/20.
Графики этих функций предлагается построить самостоятельно.
Пример 4. Бюджет потребителя 120 ден. ед., а его функция полезности
U= 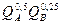 .
.
Продукт А производится по технологии, отображаемой функцией QA= 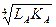 , а продукт В – QB=
, а продукт В – QB= 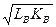 . Факторы производства фирмы покупают по неизменным ценам rL = 2; rK = 8.
. Факторы производства фирмы покупают по неизменным ценам rL = 2; rK = 8.
Какую максимальную полезность в этих условиях может достичь потребитель?
Решение.
Воспользуемся вторым законом Госсена (1.1.9). При заданной функции полезности получим 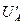 =0.5U/QA,
=0.5U/QA, 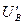 =0.25U/QB и 0.5QB/0,25QA= PA /PВ, бюджетное ограничение QA∙PA + QВ∙PВ =120. Откуда функции спроса индивида на блага получают следующий вид:
=0.25U/QB и 0.5QB/0,25QA= PA /PВ, бюджетное ограничение QA∙PA + QВ∙PВ =120. Откуда функции спроса индивида на блага получают следующий вид: 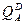 =80/PA;
=80/PA;  =40/PB.
=40/PB.
При заданной технологии и ценах факторов производства фирма А имеет  а в соответствии с условием равновесия фирмы 8KA = 2LA → KA = 0,25LA.
а в соответствии с условием равновесия фирмы 8KA = 2LA → KA = 0,25LA.
Из этих двух уравнений находим, что для производства продукции с минимальными затратами фирма А должна использовать LA = 2  и KA = 0,5
и KA = 0,5  . При этом общие затраты равны TCA = 2∙2
. При этом общие затраты равны TCA = 2∙2  + 8∙0,5
+ 8∙0,5  = 8
= 8  ; предельные затраты MCA = 16QA = PA, откуда
; предельные затраты MCA = 16QA = PA, откуда 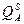 = PA/16, а фирма В имеет:
= PA/16, а фирма В имеет:
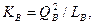 также KВ = 0,25LВ. Из этих двух уравнений находим, что для производства продукции с минимальными затратами фирма В должна использовать LВ = 2
также KВ = 0,25LВ. Из этих двух уравнений находим, что для производства продукции с минимальными затратами фирма В должна использовать LВ = 2  и KВ = 0,5
и KВ = 0,5  . При этом общие затраты равны TCВ = 2∙2
. При этом общие затраты равны TCВ = 2∙2  + 8∙0,5
+ 8∙0,5  = 8QB; предельные затраты MCB = 8 = PB.
= 8QB; предельные затраты MCB = 8 = PB.
Равновесие объемов спроса и предложения блага А достигается при
80/PA=PA/16 →PA =35,78; QA =2,236.
Благо В предлагается по неизменной цене РВ = 8, в этом случае индивид купит QВ = 40/8 = 5. Следовательно, потребитель может достичь максимальной полезности U = 2,2360,5 ∙50,25 = 2,236.
Пример 5. Предположим, что необходимо оценить работу некоторой отрасли, если известен объем производства отрасли Y, затраты трудовых ресурсов L и объем используемого капитала К:
| №n/n | Y | K | L |
| 104.8 | |||
| 117.2 | |||
| 121.9 | |||
| 115.6 | |||
| 134.2 | |||
| 139.9 | |||
| 123.2 | |||
| 142.7 | |||
| 148.1 | |||
| 156.2 | |||
| 152.2 | |||
| 155.8 | |||
| 197.5 | |||
| 201.1 | |||
| 195.9 | |||
| 194.4 | |||
| 146.4 | |||
| 160.5 |
Исходя из теоретических знаний можем предположить, что зависимость объема производства от труда и капитала описывается ПФ Кобба-Дугласа 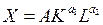 .
.
Задание: необходимо оценить значения параметров A, а1, а2 с помощью средств регрессионного анализа.
Решение:
ПФ приведем к линейному виду путем логарифмирования:
lnХ=lnA+ а1lnK+ а2lnL.
Обозначив Y= lnХ, x1=lnK, x2=lnL, a0=lnA, получим уравнение множественной регрессии: Y= a0+ а1x1+ а2x2.
С помощью сервисного пакета “Анализ данных” EXCEL оценим параметры a0, a1, a2:
a0= -0,04302 , a1=0,245099, a2=0,766056.
Вычислим параметр А. Для этого найдем экспоненту от константы регрессии А=е-0,04302=0.958.
Рассчитаем теоретические значения объема производства по формуле:
Y*=0.958K0.245L0.766 .
С помощью <Мастера диаграмм> EXCEL построим графики фактических Y и теоретических Y* значений объема производства отрасли.
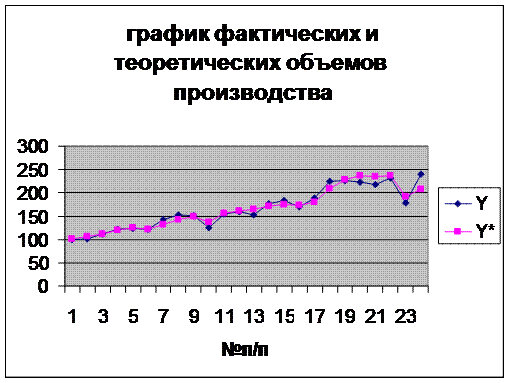
Вывод: полученная функция достаточно хорошо отражает реальные данные. Значение коэффициента детерминации R=0.955 говорит о хорошей функциональной зависимости.
Кроме того, сумма 0.245+0.766=1.011 близка к 1, поэтому можно предположить, что реальная зависимость, возможно, описывается ПФ Кобба-Дугласа.
Контрольные вопросы
1. Эконометрическое моделирование функции спроса.
2. Эконометрическое моделирование функции предпочтения.
3. Эластичность спроса по цене: определение и использование в практике маркетинга.
4. Методы оценивания эластичности спроса по цене.
5. Свойства эластичности спроса по цене.
6. Перекрестные коэффициенты эластичности.
7. Уравнение Слуцкого.
8. Взаимозаменяемые и взаимодополняемые товары.
9. Ценные и малоценные товары.
10. Графическая иллюстрация компенсированного изменения цены.
11. Один товар: кривая спроса и предложения.
12. Один товар: понятие равновесной цены, дефицит и излишек.
13. Один товар: индивидуальный и рыночный спрос.
14. Один товар: эластичный и неэластичный спрос. Определение, свойства.
15. Один товар: спрос постоянной эластичности.
16. Один товар: реакция потребителя на изменение цен в зависимости от коэффициента эластичности.
17. Реакция производителя товара в зависимости от эластичности спроса.
18. Понятие и математическая формализация потребительского выбора.
19. Использование моделей потребительского выбора для принятия управленческих решений.
20. Использование моделей спроса для принятия управленческих решений в условиях недостатка маркетинговых данных.
21. Производственная функция: основные понятия.
22. Производственная функция: экономическое содержание.
23. Производственная функция: закон убывающей доходности.
24. Производственная функция: характер изменения при расширении масштабов производства.
25. Производственная функция: средний и предельный доходы.
26. Характеристика производств в зависимости от соотношения средних и предельных доходов.
27. Предельная норма замены.
28. Производственная функция Кобба-Дугласа. Определение.
29. Производственная функция Кобба-Дугласа. Основные свойства.
30. Производственная функция Кобба-Дугласа. Экономический смысл средних и предельных показателей.
31. Производственная функция Кобба-Дугласа. Свойства показателей эластичности.
32. Производственная функция Кобба-Дугласа. Экономическая и особая области.
33. Производственная функция Кобба-Дугласа. Изокванты.
34. Понятие равновесной цены.
35. Дана производственная функция Кобба-Дугласа: Y = 1,038 K0,655 L0.345. Какова норма замены труда фондами?
36. Какой экономический смысл имеют коэффициенты А, a1, a2 мультипликативной производственной функции F(K,L) =  ?
?
37. Что такое изоклинали? В чем их экономический смысл?
38. Мультипликативная производственная функция и её свойства.
Тесты
1. Предельная производительность (предельный продукт) i – го ресурса рассчитывается по формуле:
а) 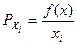 ; б)
; б) 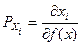 ; в)
; в) 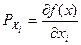 .
.
2. Что показывает коэффициент эластичности:
а) на сколько изменится факторный признак при изменении результативного признака на один процент;
б) на сколько процентов изменится результативный признак при изменении факторного признака на один процент;
в) долю изменения результативного признака под действием факторного признака.
3. Средняя производительность (средний продукт) i – го ресурса рассчитывается по формуле:
а) 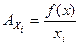 ; б)
; б) 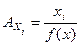 ; в)
; в)  .
.
4. Оценка эластичности потребления ресурса по объему выпускаемой продукции, находиться по формуле:
а) 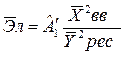 ; б)
; б) 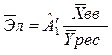 ; в)
; в) 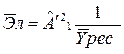 .
.
5. Функцией полезности U(x, у) называется функция
а) задающая степень полезности (для потребителя) набора товаров, состоящего из х единиц товара Х и у единиц товара Y;
б) задающая количество полезных ингридиентов в единице продукта;
в) определяющая степень полезности ресурсов для производства оптимального объема продукции.
6. Эластичность спроса зависит от факторов:
а) наличие товаров-заменителей (одним из самых неэластичных товаров является соль, т.к. ее нельзя ничем заменить);
б) удельный вес стоимости товара в бюджете потребителя;
в) размеры дохода покупателей (при этом цена может не меняться, изменяется платежеспособность – чем дороже товар, тем эластичнее спрос на него);
г) качество товара (чем выше качество, чем менее эластичен спрос);
д) п.п. а-г.
7. Свойством эластичности является:
а) Эластичность суммы у=у1+…+уп положительных функций уi удовлетворяет соотношению Еmin £ Еу £ Еmax, где Еmin(Еmax) – это минимальная (максимальная) эластичность функций уi.
б) Эластичность произведения функций u=u(x) и v=v(x) равна рзности эластичностей функций u и v: Еuv = Еu – Еv.
в) Эластичность частного функций u=u(x) и v=v(x) равна сумме эластичностей функций u и v: Еuv = Еu + Еv..
8. Свойством эластичности является:
а) Эластичность произведения функций u=u(x) и v=v(x) равна произведению эластичностей функций u и v: Еuv = Еu ∙ Еv.
б) Эластичность частного функций u=u(x) и v=v(x) равна разности эластичностей функций u и v: Еuv = Еu – Еv..
в) Для сложной функции у=у(х(t)) эластичность у по t удовлетворяет равенству Еyt = Еyx /Еxt..
9. Свойством эластичности является:
а) Эластичность произведения функций u=u(x) и v=v(x) равна разности эластичностей функций u и v: Еuv = Еu – Еv.
б) Эластичность частного функций u=u(x) и v=v(x) равна сумме эластичностей функций u и v: Еuv = Еu + Еv..
в) Эластичность обратной функции удовлетворяет соотношению Еxy=1/Еyx..
10. Свойством эластичности является:
а) Эластичность произведения функций u=u(x) и v=v(x) равна разности эластичностей функций u и v: Еuv = Еu – Еv.
б) Эластичность частного функций u=u(x) и v=v(x) равна сумме эластичностей функций u и v: Еuv = Еu + Еv..
в) Для сложной функции у=у(х(t)) эластичность у по t удовлетворяет равенству Еyt = Еyx ∙Еxt..
11. Производственная функция типа Кобба-Дугласа записывается в виде:
а) у=Ах 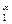 +Вх
+Вх 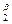 ; б) у=Ах
; б) у=Ах 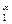 х
х 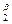 ; в) у=Ах
; в) у=Ах 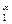 /Вх
/Вх 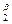 .
.
12. Производственная функция записывается в виде Y=f (x1,x2), где
а) x1 –стоимость основных производственных фондов, x2 – объём выпускаемой продукции, Y– численность промышленно-производственного персонала;
б) x1 – стоимость товарной продукции, x2 – численность промышленно-производственного персонала, Y– стоимость основных производственных фондов;
в) x1 –стоимость основных производственных фондов, x2 – численность промышленно-производственного персонала, Y– стоимость товарной продукции.
13. К характеристикам производственной функции относятся:
а) предельная производительность ресурса;
б) предельная производительность ресурса;
в) эластичность замещения ресурсов;
г) средняя норма замещения ресурсов;
14. При росте объема производства изокванта будет смещаться:
а) вверх и вправо; в) вверх и влево;
б) вниз и вправо; г) вниз и влево.
15. Эластичность спроса на ресурс зависит от:
а) эластичности спроса на продукт;
б) соотношения издержек на труд и общих издержек;
в) верны а) и б);
г) ни один из перечисленных факторов не влияет на эластичность спроса на ресурс.
16. Дана производственная функция Q(L,K)=5L0,3K0,5. Для нее характерна:
а) возрастающая экономия от масштаба;
б) постоянная экономия от масштаба;
в) убывающая экономия от масштаба;
г) ничего определенного сказать нельзя.
17. Предельная норма технического замещения труда капиталом равна 1/2. Для того чтобы обеспечить предельный объем производства при увеличении капитала на 4 единицы, необходимо сократить использование труда:
а) на 2 единицы; в) на 8 единиц;
б) на 4 единицы; г) необходима дополнительная информация.
18. Когда предельная производительность падает, экономия от масштаба:
а) возрастает; в) постоянна;
б) убывает; г) данных недостаточно.
19. Изокванта объединяет точки:
а) равных издержек;
б) одинакового выпуска продукции;
в) устойчивого равновесия производителя;
г) равенства спроса и предложения.
20. Когда предельная производительность растет, экономия от масштаба:
а) возрастает; в) постоянна;
б) убывает; г) данных недостаточно.
Ответы к тестам
| 1) в | 6) д |
| 2) б | 7) а |
| 3) а | 8) б |
| 4) б | 9) в |
| 5) а | 10) в |
| 11) б | 16) в |
| 12) в | 17) а |
| 13) в | 18) г |
| 14) а | 19) б |
| 15) г | 20) г |
Задания и задачи
Задача 1. Функция полезности индивида: u =(QA + 4)(QB + 5), где QA, QB – количества двух различных благ, его бюджет: М = 64, а цены благ pA = 1, pB = 1.5. Запишите уравнение кривой безразличия, на которой находится потребитель в момент равновесия.
Задача 2. Функция спроса на газ имеет вид QD = 3.75pn – 5pg, а функция его предложения – QS = 14 + 0.25pn + 2pg, где pn, pg – соответственно цены нефти и газа. При каких ценах на данные энергоносители объемы спроса и предложения газа будут равны 20 ед.?
Задача 3. В условиях задачи 2 определить, на сколько процентов изменится объем продажи газа при увеличении цены нефти на 25%.
Задача 4. На рынке данного товара функция спроса описывается уравнением: QD = 6 – P, функция предложения: QS = –3 + 2P, где QD – объем спроса, млн. шт. в год; QS – объем предложения, млн. шт. в год;
а) определите равновесную цену и равновесный объем продажи;
б) если цена данного товара будет составлять 2 ден. ед., что образуется на рынке: излишек или дефицит товара? В каком размере?
в) какая ситуация будет на рынке, если цена возрастет до 4 ден. ед.?
Задача 5. Опытным путем установлены функции спроса q = (p+8)/(p+2) и предложения s = p + 0,5 , где q и s – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени, p – цена товара. Найти: а) равновесную цену, т.е. цену, при которой спрос и предложение уравновешиваются; б) эластичность спроса и предложения для этой цены; в) изменение дохода при увеличении цены на 5% от равновесной.
Задача 6. Функции спроса q и предложения s от цены p выражаются соответственно уравнениями q = 7 – p и s = p + 1. Найти: а) равновесную цену; б) эластичность спроса и предложения для этой цены; в) изменение дохода (в процентах) при увеличении цены на 5% от равновесной.
Задача 7. Как связаны предельные и средние полные затраты предприятия, если эластичность полных затрат равна 1?
Задача 8. Спрос на товар А (яблоки) описывается уравнением QdА=100 – 2РА + РВ; спрос на товар В (груши) – уравнением QdВ =100–2PВ+PА. Предложение товара А описывается уравнением QsА = –50 + РА; предложение товара В – уравнением QsB = –50 + PB.
Задача 9. Определите параметры рыночного равновесия на двух рынках; как изменятся параметры рыночного равновесия, если на товар В (груши) будет введен налог в размере 10 ден. ед. за единицу товара; выгодно ли государству это делать. Рассчитайте изменение общественного благосостояния. Сравните потери общественного благосостояния в случае, если такой налог будет введен на двух рынках одновременно.
Задача 10. Потребитель выделил на приобретение двух товаров 3300 д.е. Цена первого товара 15 д.е., второго – 22 д.е. Функция полезности потребителя – U(x,y) = 60x + 90y. Записать задачу потребителя.
Задача 11. Потребитель выделил на приобретение двух товаров 3300 д.е. Цена первого товара 15 д.е., второго – 22 д.е. Функция полезности потребителя – U(x,y) = 60x + 90y. Изобразить геометрически бюджетное множество, отметить бюджетную линию.
Задача 12. Потребитель выделил на приобретение двух товаров 3300 д.е. Цена первого товара 15 д.е., второго – 22 д.е. Функция полезности потребителя – U(x,y) = 60x + 90y. Изобразить геометрически кривую безразличия U(x,y) = 4500.
Задача 13. Потребитель выделил на приобретение двух товаров 3300 д.е. Цена первого товара 15 д.е., второго – 22 д.е. Функция полезности потребителя – U(x,y) = 60x + 90y. Какова предельная полезность потребителя по каждому товару?
Задача 14. Потребитель выделил на приобретение двух товаров 3300 д.е. Цена первого товара 15 д.е., второго – 22 д.е. Функция полезности потребителя – U(x,y) = 60x + 90y. Решить задачу потребителя.
Задача 15. Потребитель выделил на приобретение двух товаров 3300 д.е. Цена первого товара 15 д.е., второго – 22 д.е. Функция полезности потребителя – U(x,y) = 60x + 90y. Определить максимальную полезность потребителя от потребления этих двух товаров.
Задача 16. Спрос потребителя на некоторый товар в зависимости от цены определяется функцией d(p) = –0,3p + 60. Определить коэффициент ценовой эластичности при p = 120, p = 60.
Задача 17. Спрос потребителя на некоторый товар в зависимости от цены определяется функцией d(p) = –0,3p + 60. При какой цене коэффициент эластичности равен единице?
Задача 18. Спрос потребителя на некоторый товар в зависимости от цены определяется функцией d(p) = –0,3p + 60. Эластичен ли спрос при p = 120, p = 60?
Задача 19. Исследовался спрос на товар двух групп потребителей. Функции спроса в зависимости от цены, предъявляемые каждой группой, имеют вид: d1(p) = –0,2p + 80, d2(p) = –0,4 + 60. Построить совокупную функцию спроса.
Задача 20. Исследовался спрос на товар двух групп потребителей. Функции спроса в зависимости от цены, предъявляемые каждой группой, имеют вид: d1(p) = –0,2p + 80, d2(p) = –0,4 + 60. Чему равен совокупный спрос при p = 100 д.е., p = 200 д.е.?
Задача 21. Исследовался спрос на товар двух групп потребителей. Функции спроса в зависимости от цены, предъявляемые каждой группой, имеют вид: d1(p) = –0,2p + 80, d2(p) = –0,4 + 60. Изобразить геометрически спрос каждой группы и совокупный спрос.
Задача 22. Для трех видов продукции А, В и С модели зависимости удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом: yA = 600, yВ = 80 + 0,7х, yС= 40х0,5. Определить коэффициенты эластичности по каждому виду продукции.
Задача 23. Фирма работает в условиях совершенной конкуренции: выпускает один вид продукции, используя при этом два вида ресурсов. Производственная функция фирмы равна f(x,y) = 80xy, цена реализации продукции – 120 д.е., ресурсы приобретаются по ценам W1 = 20 д.е., W2 = 15 д.е. соответственно.
а) Записать функцию прибыли.
б) Записать условия максимума прибыли.
в) Решить задачу фирмы максимизации прибыли.
г) Построить изокванту f(x,y) = 6400.
д) Построить изокосту C(x,y) = 3000.
Задача 24. Предприятие вырабатывает игрушки, которые продает на совершенно конкурентном рынке по 5 ден. ед. за штуку. Производственная функция задана уравнением Q = 30L – 0,5L2, где Q – количество игрушек за месяц; L – количество рабочих, чел. Напишите формулу для вычисления стоимости предельного продукта труда на данном предприятии. Если текущая ставка заработной платы составляет 50 ден. ед. в месяц, сколько рабочих наймет предприятие? Если заработная плата в данном регионе увеличится до 100 ден. ед. и предприятие вынужденное будет и себе повысить ставку заработной платы, как в результате изменятся экономические показатели предприятия: объем производства, прибыль, занятость. При какой ставке заработной платы предприятие вынужденное будет остановиться?
Задача 25. Рассмотрим ПФ X = 2.341K0.264L0.678 и показатели экономики некоторой страны: валовой продукт возрос с 2000 по 2009 г. в 1.47 раза, ОПФ за этот же период увеличились в 1.88 раза, а число занятых – в 1.24 раза. Вычислить по ней масштаб и эффективность производства.
Задача 26. Для ПФ Кобба-Дугласа (Задача 3) найти в явном виде нормы замещения фондов трудовыми ресурсами и трудовых ресурсов фондами.
Задача 27. Производственная функция фирмы описывается функцией Кобба-Дугласа 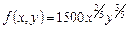 , где x – затраты капитала, y – затраты труда. а) Рассчитать выпуск при x = 243, y = 32.
, где x – затраты капитала, y – затраты труда. а) Рассчитать выпуск при x = 243, y = 32.
б) Рассчитать предельную и среднюю производительность труда при x= 243, y = 32.
в) Рассчитать предельную и среднюю фондоотдачу при x = 243, y = 32.
Задача 28. Производственная функция фирмы имеет следующий вид:
X= –4 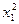 +24х1+ 2x1x2+6x2 –
+24х1+ 2x1x2+6x2 – 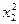 ,
,
где x1, x2 – затраты ресурсов. Определить максимальный выпуск и обеспечивающие этот выпуск затраты ресурсов.
Задача 29. Производственная функция вида:
X=5 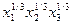 описывает зависимость между затратами ресурсов x1, x2, x3 и выпуском X. Определить максимальный выпуск, если x1+ x2+ x3=9. Каковы предельные продукты в оптимальной точке?
описывает зависимость между затратами ресурсов x1, x2, x3 и выпуском X. Определить максимальный выпуск, если x1+ x2+ x3=9. Каковы предельные продукты в оптимальной точке?
Задача 30. Производственная функция фирмы имеет следующий вид:
X=3 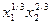 .
.
Определить предельные продукты по ресурсам и построить изокванту Х=3. Найти норму замены первого ресурса вторым в точке x1+ x2=1.
Дата добавления: 2020-10-25; просмотров: 653;











