Перекрестные коэффициенты эластичности.
В 1.1.2 было введено понятие эластичности функции одной переменной. Аналогично вводится понятие эластичности функции нескольких переменных. Пусть, например, z =f(x, у) – функция двух переменных.
Еzx –коэффициент эластичности z по х показывает, на сколько процентов изменится z при увеличении х на один процент. Еzу – коэффициент эластичности z по у показывает, на сколько процентов изменится z при увеличении y на один процент.
Из определения вытекают следующие формулы:
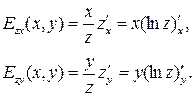 (1.1.2)
(1.1.2)
Пример1.1.2. Найти коэффициенты эластичности по х и по у функции z= xy в точке (2;3).
Согласно формулам (1.1.2) имеем
Еzx(х,у) = x(lnz)'x = x(ylnx)'x= у,
Ezy(x,y) = y(lnz)'y = y(ylnx)'y =уlnх.
Следовательно, Еzx(2,3) =3, Еzy(2;3) = 3ln 2.
Формулы (1.1.2) полностью аналогичны формулам, которые использовались при выводе свойств 1–3 эластичности в 1.1.2. Поэтому первые три свойства эластичности справедливы и в случае функции нескольких переменных. Четвертое и пятое свойства также сохраняются, но формы их записи становятся сложнее. Остановимся подробнее на этих свойствах.
Свойство 4'. Для функций z =f(x, у), х = j(t) и у = y(t) эластичность z no t в точке t0 находится по формуле
Еzt = ЕzxЕxt + ЕzyЕyt , (1.1.3)
где Еzx, Еzy – эластичности z по х и у в точке (j(t0), y(t0)), а Еxt, Еyt –эластичности х и у по t в точке t0.
Для любой пары функций у1=f1(х1, х2), y2=f2(x1, x2) имеем 4 коэффициента эластичности, которые запишем в матрицу размера 2х2:
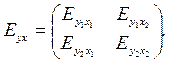
Элементы этой матрицы, расположенные вне главной диагонали, называютсяперекрестными коэффициентами эластичности.
Свойство 5'.Пусть х1=g1(y1, y2), x2=g2(y1, y2) – пара обратных функций для функций у1=f1(х1, х2), y2=f2(x1, x2). Тогда матрица коэффициентов эластичности Еxy является обратной к матрице Еyx.
Коэффициенты эластичности используются при анализе функций спроса при любом числе различных товаров. В качестве примера рассмотрим случай с двумя товарами. Пусть хi – количество i-го товара, рi – его цена (i= 1,2). Для пары дополняющих товаров (например, чай и сахар) или заменяющих товаров (например, масло и маргарин) естественно считать, что спрос на каждый товар зависит от обеих цен р1 и р2:
х1=D1(p1, p2), x2=D2(p1, p2) (1.1.4)
Предположим, что не только цены определяют спрос, но и, напротив, спрос определяет цены. Иными словами, будем считать, что систему (1.2.4) можно разрешить относительно р1 и р2 в следующем виде:
p1=p1(х1, х2), p2=p2(x1, x2). (1.1.5)
Системы (1.1.4) и (1.1.5) определяют две пары взаимно обратных функций. Согласно свойству 5' матрица коэффициентов эластичности цен по спросу может быть найдена как обратная матрица коэффициентов эластичности спроса по цене.
Пример1.1.3. Пусть х1=10p1-1.2 p20.8, x2=12p1-0.9p2-0.7. (x1 – маргарин, x2 – масло). Коэффициенты эластичности составят матрицу
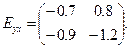
Спрос на маргарин неэластичный, на масло – эластичный, перекрестные коэффициенты эластичности показывают, что маргарин заменяет масло – повышение цены на масло на 1% ведет к повышению спроса на маргарин на 0.8%. Чтобы получить коэффициенты эластичности цены по спросу Еху,достаточно найти обратную матрицу Еуx-1.
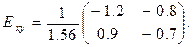
Дата добавления: 2020-10-25; просмотров: 600;











