Основные положения теории БЭТ

1. поверхность энергетически однородна

2. адсорбция локализована

3. теплота адсорбции во 2 ,3 ……n слоях постоянна и равна теплоте конденсации: ∆Н_{адс 2 ,3 ……n} = const и = ∆Н_конд

_А

1 Р/Р_о

Теория предполагает образование полислоя на поверхности адсорбента, но из понятия однородности поверхности следует, что друг с другом молекулы адсорбата не должны взаимодействовать. Можно заранее сказать, что уравнение БЭТ строго описывает адсорбцию только в монослое.

Вывод уравнения ( не даю)

В теории БЭТ сделано предположение т образовании на поверхности адсорбента последовательных комплексов центров адсорбции с 1,2,3 и т.д. молекулами адсорбата.

Процесс адсорбции можно представить в виде последовательных квазихимических реакций:

А + В = АВ АВ + В = АВ₂ АВ₂ + В = АВ₃

Константы равновесия для этих реакций соответственно равны:

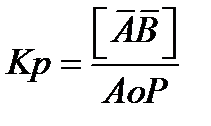
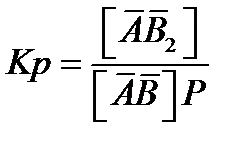
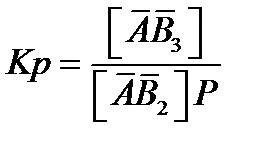(2.80)

где А_о — концентрация свободных центров.

Для концентрации соответствующих комплексов можно записать:

[АВ] = К_р А_о Р (2.81)

[АВ₂] = К₁ [АВ] Р = К₁ К_р А_о Р² (2.82)

[АВ₃] = К₂ [АВ₂] Р = К₁ К₂К_р А_о Р³ (2.83)

Авторы приняли, что во всех слоях, кроме 1-го, молекулы адсорбата взаимодействуют между собой как при конденсации, и следовательно:

k₁ = k₂ = k_L = A_ж/A_п = 1/P_о (2.84)

Для упрощения введем обозначение:

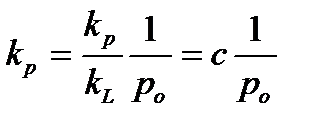, х=р/р_о (2.85)

постоянная с характеризует разность ∆G (энергии Гиббса) процессов адсорбции и конденсации.

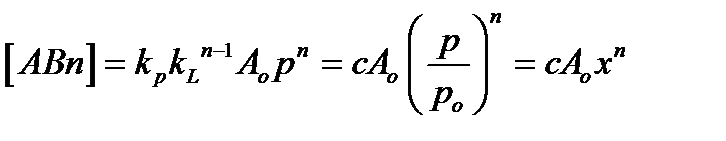
(2.86)

или возвращаясь к предыдущему:

[АВ] = А_о с х (2.87)

[АВ₂] = А_о с х² (2.88)

[АВ₃] = А_о с х³ … и т.д. (2.89)

Общее число центров:

А_∞= А_о + [АВ] + [АВ₂] + [АВ₃] …= А_о + А_о с х + А_о с х² + А_о с х³ …= А_о [1 + сх + (1 + х + х²…) ] (2.90)

В круглых скобках имеем геометрическую прогрессию, которую при х<1 равна

∑ = 1/(1—х), отсюда:

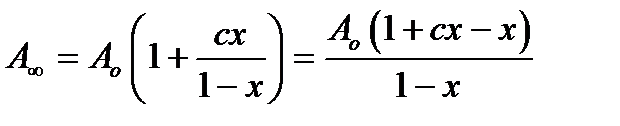(2.91)

Величина адсорбции молекул адсорбата :

А = [АВ] + 2[АВ₂] + 3[АВ₃] +…= А_о с х (1 + 2х + 3х²…) ] (2.92)

Ряд 1 + 2х + 3х² можно представить как производную от выражения (1 + х + х²…):

1 + 2х + 3х² = (1 + х + х²…)′ (2.93)

∑ 1 + 2х + 3х² = 1/(1—х)² (2.94)

подставляя в 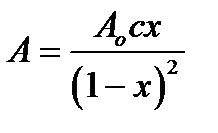значения для А_о и с, получаем выражение,

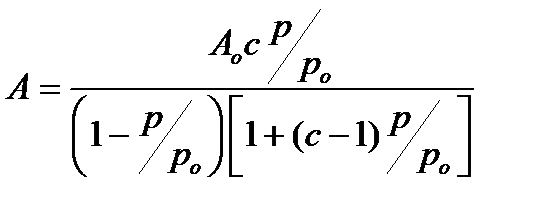(2.95)

Обычно уравнение БЭТ представляют в следующем виде:

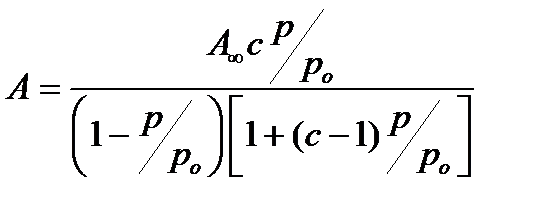(2.96)

оно содержит две константы А_∞ — фактически емкость монослоя и с, которая равна отношению констант адсорбции к константе конденсации (с= k _адс/ k _конд.).

Анализ уравнения приводит к следующим выводам:

При р/р_о много <1 получаем А= А_∞с р/р_о — линейная зависимость, предельный случай, закон Генри. (Уравнение БЭТ переходит в уравнение Ленгмюра, а затем в закон Генри).

Экспериментальные данные по адсорбции согласуются с теорией тем лучше, чем больше значения с и теплоты адсорбции. Этому способствует увеличение сродства адсорбата к адсорбенту и уменьшению взаимодействия между молекулами адсорбата.

Уравнение БЭТ лучше описывает адсорбцию в интервале давлений адсорбата: 0,05 < р/р_о <0,3. Меньшая величина связана с искажениями, вносимыми неоднородностью поверхности, большая — связана с взаимодействиями между молекулами адсорбата. Поэтому уравнение, выведенное для полимолекулярной адсорбции газов, лучше всего описывает мономолекулярную адсорбцию.

Для точного определения А_∞ и с используют линейную форму уравнения: 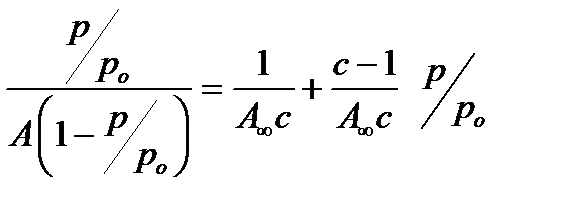(2.97)

следовательно, графически экспериментальные данные в соответствующих координатах описываются линейной зависимостью:

\

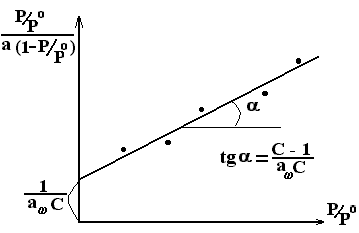
Рис. 2.27. Линейный график уравнения БЭТ

Из системы двух уравнений с двумя неизвестными легко определить искомые величины А_∞ и С.

На теории БЭТ основан стандартный метод измерения удельной поверхности адсорбентов, катализаторов, порошков и т.д.

В качестве адсорбатов используют с этой целью инертные газы (N₂, Kr, Ar), которые проявляют слабое межмолекулярное взаимодействие на поверхности адсорбента. Для увеличения адсорбции таких газов ее ведут при низких температурах (низкотемпературная адсорбция).

Предложено много модификаций теории БЭТ, но они описывают только частные варианты. Трудно исправить недостатки, не нарушив простоты вывода и пользования — явных достоинств этой теории.