Репрезентативность при изучении качественных признаков
Качественные признаки обычно не могут иметь градаций проявления: они или имеются, или не имеются у каждой из особей, например пол, комолость, наличие или отсутствие каких-нибудь особенностей, уродств, выдающихся качеств, хромосомных перестроек, точечных мутаций, заболеваний, исходов болезней и т. д.
Принципиальной разницы между количественными и качественными признаками нет. Степень проявлений большинства качественных признаков при более тщательном исследовании может быть измерена, и тогда качественный признак становится количественным. И, наоборот, любой количественный признак может быть выражен в альтернативной форме (например, больше средней и меньше средней) и тогда он для исследователя превратится в качественный признак.
При изучении групповых свойств по качественным признакам характеристика группы заключается в указании числа плюсовых и минусовых объектов, т. е. объектов, имеющих и не имеющих признак.
Основные сводные показатели: средняя величина и стандартное отклонение качественных признаков имеют, конечно, свои специфические особенности и по технике их расчета и по способам использования в биологических работах.
Средняя величина качественного признака в группе – это доля плюсовых объектов, определяемая по формуле:
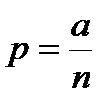 ; (10.21)
; (10.21)
где р – выборочная доля плюсовых объектов (имеющих изучаемый качественный признак);
а – количество плюсовых объектов в группе;
n – объем группы.
Если группа состоит из 200 особей, из которых 120 самок, то доля самок в группе:
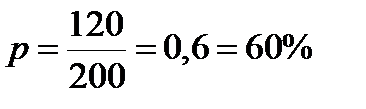 .
.
Если долю умножить на 100, то получится характеристика, выраженная в процентах.
В генеральной совокупности доля плюсовых объектов выражается такой формулой:
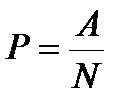 , (10.22)
, (10.22)
где Р – доля плюсовых объектов в генеральной совокупности;
А – количество плюсовых объектов;
N – объем генеральной совокупности.
Сумма квадратов центральных отклонений или дисперсия качественных признаков определяется по формулам:
В выборках – C = npq; (10.23)
В генеральных совокупностях – 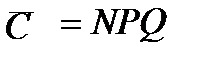 ; (10.24)
; (10.24)
где q = 1 – p; Q = 1 – P – доля минусовых объектов в выборке и в генеральной совокупности.
При n = 200, а = 120, p = 0,6, q = 0,4
С = 200 × 0,6 × 0,4 = 48.
Стандартное отклонение качественных признаков определяется по формулам:
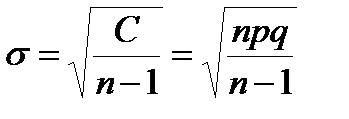 ; (10.25)
; (10.25)
 . (10.26)
. (10.26)
Стандартное отклонение качественных признаков имеет принципиальное отличие от сигмы количественных признаков. Произведение pq = p (1 – р) не может быть больше одной четверти:
max [pq] = 0,25 (10.27)
Эта максимальная величина произведения доли на свое дополнение до единицы получается при р = 0,5 и равна 0,5 × 0,5 = 0,25. Всякое другое произведение дает уже меньшую величину, например при р = 0,4; рq = 0,4×0,6 = 0,24.
Поэтому и стандартное отклонение качественных признаков не может быть больше определенного предела: в выборках:
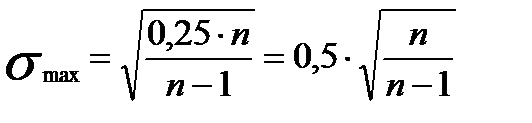 . (10.28)
. (10.28)
В генеральных совокупностях:
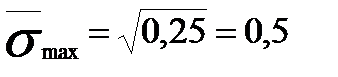 (10.29)
(10.29)
Наличие верхнего предела сигмы значительно упрощает планирование достаточной численности выборки при изучении качественных признаков.
Ошибка репрезентативности доли аналогична ошибке средней и определяется по формуле:
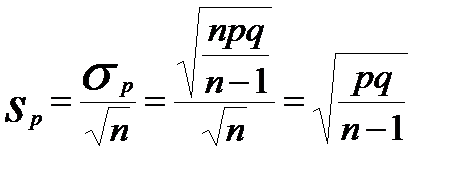 , (10.30)
, (10.30)
Например: при n = 200, а = 120, p = 0,6, q = 0,4
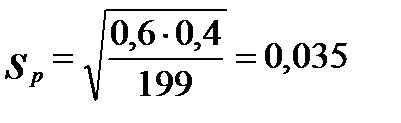 .
.
Максимально возможное значение ошибки:
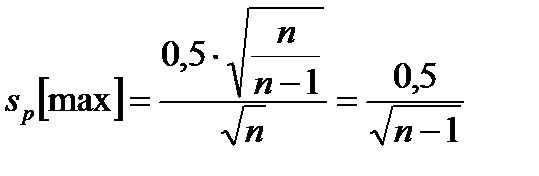 .
.
Если в выборке получены крайние значения доли (или 0 или 1, т. е. когда в выборке нет ни одного плюсового объекта или, наоборот, вся выборка состоит из одних плюсовых объектов), то ошибка таких долей определяется по формуле:
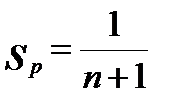 ,
, 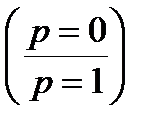 (10.31)
(10.31)
Если в выборке из 9 объектов не оказалось ни одного плюсового, то р = 0, а sр = 1/10 = 0,1.
В некоторых биологических исследованиях генеральные доли известны или предполагаются известными и все же требуется определить ошибку выборочной доли для выборок разного объема. В таких случаях ошибка доли определяется по точной формуле:
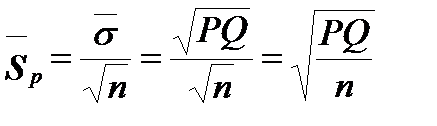 , (10.32)
, (10.32)
где в числителе подкоренного выражения стоит произведение генеральной доли на ее дополнение до единицы, а в знаменателе – полный объем выборки (а не число степеней свободы).
Оценка генеральной доли, или определение ее доверительных границ, производится так же, как и оценка генеральной средней:
Р = р ± D; D = t × sp (10.33)
где Р, р – генеральная и выборочная доли;
D = tst × sp – возможная максимальная погрешность при прогнозе генерального параметра;
tst – критерий надежности для трех порогов вероятности безошибочных прогнозов (b1=0,95, b2=0,99, b3=0,999) устанавливается так же как и при оценке генеральной средней; или по таблице стандартных значений критерия Стьюдента или по приближенным формулам;
sр – ошибка репрезентативности выборочной доли (показатель точности).
Пример
При исследовании 200 особей одного вида у 60 из них сказалась повышенная способность выдерживать сильное понижение температуры среды обитания. Как часто такие особи могут встретиться среди всей популяции?
Для решения этого вопроса достаточно определить доверительные границы генеральной доли; при сходных данных
n = 200, a = 60, 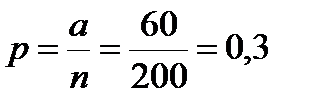 ;
; 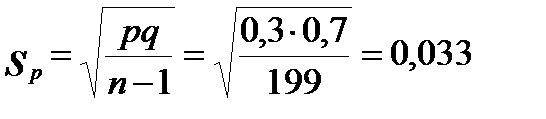 ;
;
b1 = 0,95; n = 199; tst = 2,0; D = tst × sp=2,0 × 0,033=0,066;
p = 0,3 ± 0,066 [не более 0.3 + 0,066 = 0,366 ~ 37%; не менее
0.3 – 0,066 = 0,234 ~ 24%.
Дата добавления: 2020-10-25; просмотров: 564;











