Теорема о среднем значении
Теорема о среднем значении: Пусть функции 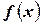 и
и 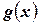 непрерывны на отрезке
непрерывны на отрезке 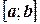 и
и 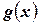 знакопостоянна на этом отрезке. Тогда
знакопостоянна на этом отрезке. Тогда 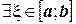 , такая что
, такая что
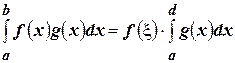 . (4.24)
. (4.24)
Доказательство:
Пусть для определённости 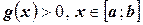 . Функция
. Функция 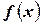 на отрезке
на отрезке 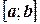 удовлетворяет условиям теоремы Вейерштрасса. Следовательно, на этом отрезке она достигает своих наибольшего и наименьшего значений, т. е.
удовлетворяет условиям теоремы Вейерштрасса. Следовательно, на этом отрезке она достигает своих наибольшего и наименьшего значений, т. е. 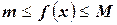 . Умножим это неравенство на
. Умножим это неравенство на 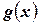 . В результате получим
. В результате получим 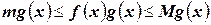 . Теперь проинтегрируем это неравенство:
. Теперь проинтегрируем это неравенство:
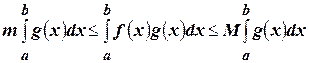 . (4.25)
. (4.25)
Анализируя (4.25), приходим к выводу, что 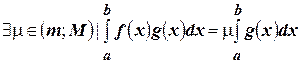 . По теореме о принятии функцией, непрерывной на отрезке, любого промежуточного значения:
. По теореме о принятии функцией, непрерывной на отрезке, любого промежуточного значения: 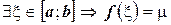 . Подставим вместо
. Подставим вместо 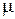 значение
значение 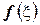 , получим
, получим
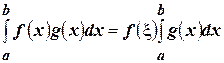 . ☻
. ☻
Замечания:
1). Если 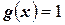 , то соотношение (4.24) принимает вид
, то соотношение (4.24) принимает вид
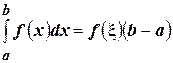 .
.
Следовательно,
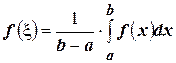 . (4.26)
. (4.26)
Значение функции 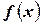 , вычисленное по формуле (4.26), принято называть средним значением функции
, вычисленное по формуле (4.26), принято называть средним значением функции 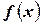 на отрезке
на отрезке 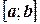 .
.
2). Если 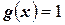 , то неравенство (4.25) принимает вид
, то неравенство (4.25) принимает вид
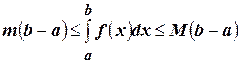 . (4.27)
. (4.27)
Неравенство (4.27) может использоваться для оценки значения определённого интеграла. Например, требуется оценить значение интеграла 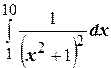 . Легко определить, что наибольшее на отрезке
. Легко определить, что наибольшее на отрезке 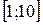 значение подынтегральной функции равно 0,25, а наименьшее -
значение подынтегральной функции равно 0,25, а наименьшее - 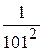 . Поэтому
. Поэтому 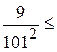
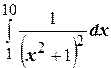
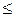
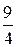 .
.
Дата добавления: 2020-10-25; просмотров: 531;











