Определенный интеграл с переменным верхним
Пределом. Теорема Барроу
Пусть 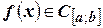 и
и 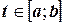 . Рассмотрим определённый интеграл с переменным верхним пределом
. Рассмотрим определённый интеграл с переменным верхним пределом
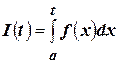 . (4.28)
. (4.28)
Теорема Барроу: Интеграл (4.28) является первообразной для подынтегральной функции, т.е. 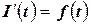 .
.
Доказательство:
По определению производной:
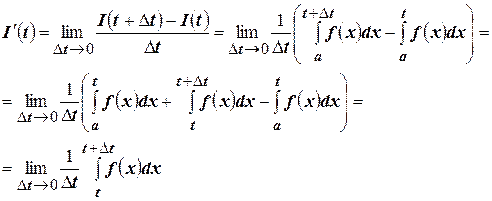
Воспользуемся теоремой о среднем значении:
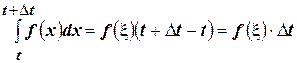
Так как 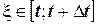 , то при
, то при 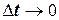 и
и 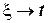 . Тогда
. Тогда
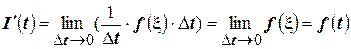 ,
,
что и требовалось доказать. ☻
Замечание:
Пусть 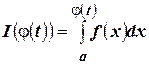 , тогда по теореме о дифференцировании сложной функции
, тогда по теореме о дифференцировании сложной функции 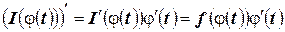 . Например, производная от интеграла
. Например, производная от интеграла 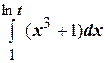 равна
равна 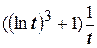 .
.
Формула Ньютона-Лейбница
Пусть 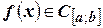 и
и 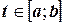 . И пусть
. И пусть 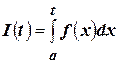 . Если функция
. Если функция 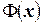 - некоторая первообразная для подынтегральной функции, то по теореме об общем виде первообразных:
- некоторая первообразная для подынтегральной функции, то по теореме об общем виде первообразных: 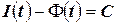 . Положим
. Положим 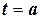 , тогда
, тогда 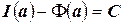 . Но
. Но 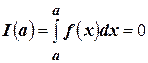 , следовательно,
, следовательно, 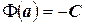 . Получили соотношение
. Получили соотношение 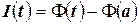 . Положим теперь в этом выражении
. Положим теперь в этом выражении 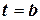 . В итоге получаем формулу
. В итоге получаем формулу
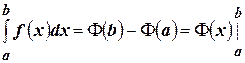 . (4.29)
. (4.29)
Формулу (4.29) называют формулой Ньютона-Лейбница. Эта формула является основной при вычислении определённых интегралов.
Пример: 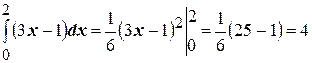
Замена переменных в определенном интеграле
 ,
,
где функция 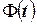 является первообразной для подынтегральной функции
является первообразной для подынтегральной функции 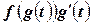 .
.
Дата добавления: 2020-10-25; просмотров: 590;











