РАСЧЕТ ПРОСТРАНСТВЕННЫХ УГЛОВ И РАДИУСОВ ИСКРИВЛЕНИЯ СТВОЛА СКВАЖИНЫ

Для определения положения ствола скважины в подземном пространстве, степени искривления ствола и его направления при дальнейшем бурении проводят инклинометрию. По данным инклинометрии вычерчивают планы, профили или изометрические графики ломаной линии, которая изображает модель ствола скважины в пространстве (рис. 22). По данным инклинометрии в точках замеров можно рассчитать также пространственные углы, а по ним - радиусы искривления ствола.

Для вывода формулы, по которой можно определить про­странственные углы искривления ствола скважины, вводятся обозначения из рис. 22, где АОВ - модель участка ствола скважины, построенная в масштабе по данным инклинометрии; α₁ - угол отклонения от вертикали отрезка ствола скважины АО; α₂ - угол отклонения от вертикали отрезка OB; ∆φ - из­менение азимута между направлениями отрезков АО и ОВ; α₀ -пространственный угол искривления модели ствола скважины в точке 0 [25].

Для треугольника АОД имеем

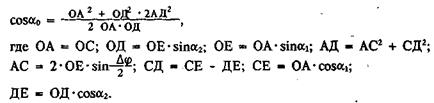
После преобразований получаем

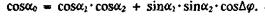
Достаточно точно пространственный угол между двумя прямыми отрезками можно определить по формуле

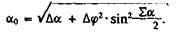
На рис. 23 представлена номограмма, с помощью которой можно определить пространственные углы искривления ствола скважин (левая часть номограммы). Ключ для вычислений при­веден с левой стороны номограммы.

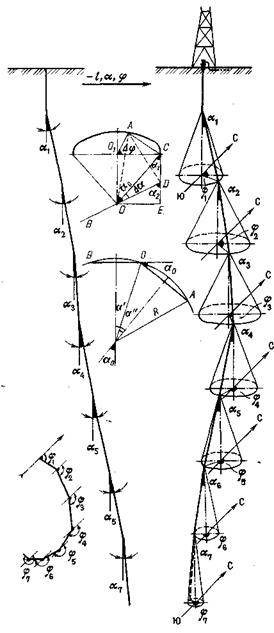
Рис. 22. Траектория ство­ла ННС по данным инклинометрии

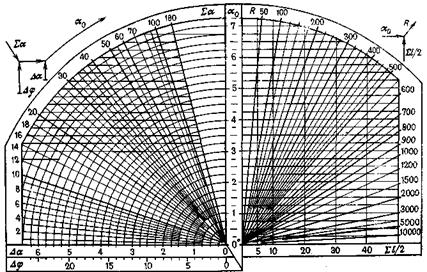
Рис. 23. Номограмма для определения пространственного угла и радиуса искривления скважины

Для определения радиуса кривизны ствола скважины между точками АОВ (см. рис. 22) составляем уравнения

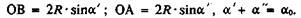
Принимая ОВ = l₁, ОА = l₂, находим

По правой части номограммы можно определить радиус кри­визны участка ствола скважины. Ключ для решения приведен с правой стороны номограммы.