Турбулентный пограничный слой на плоской пластине
Турбулентное течение является наиболее распространенной формой движения теплоносителя в теплообменных аппаратах. Теплообмен между стенкой и потоком осуществляется через пограничный слой, который оказывает основное сопротивление теплопереносу. Процессы, протекающие в нем, сводятся к переносу импульса и тепла, что непосредственно отражается на закономерностях распределения осредненной скорости и температуры. Поэтому по ним можно судить не только об интенсивности переноса импульса и тепла, но и об особенностях вихревой структуры.
Турбулентный пограничный слой на пластине можно рассчитать на основании приведенных ниже уравнений так же, как ламинарный пограничный слой, если знать выражения для mТ и lТ:
| уравнение неразрывности | 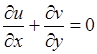 ; (2.25) ; (2.25)
|
| уравнение движения | 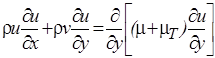 ; (2.26) ; (2.26)
|
| уравнение энергии | 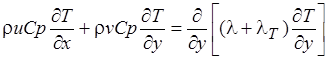 , (2.27) , (2.27)
|
причем граничными условиями будут:
u = v = 0, T=Tw при у = 0; (2.28)
u = U∞, T=T¥ при y®¥.
 |
Для замыкания данной системы уравнений применяются различные модели турбулентности.
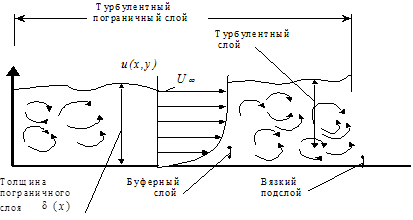
Рис. 2.2.Турбулентный пограничный слой на плоской пластине
В основу анализа закономерностей переноса импульса и тепла положено общепринятое разделение течения в турбулентном пограничном слое на пластине на две области: пристенную, или внутреннюю, часть пограничного слоя и его внешнюю часть (рис. 2.2). Пристенная область занимает около 0,2 толщины всего пограничного слоя, и течение в ней описывается так называемым законом стенки. Обычно принимают, что распределение средней скорости в пристенной области определяется величиной касательного напряжения на стенке 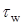 , плотностью r, кинематической вязкостью n и расстоянием от стенки y и может быть выражено законом подобия
, плотностью r, кинематической вязкостью n и расстоянием от стенки y и может быть выражено законом подобия 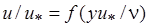 , (2.29)
, (2.29)
где 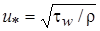 - динамическая скорость,
- динамическая скорость, 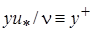 - безразмерное расстояние.
- безразмерное расстояние.
В пристенной области около самой стенки примерно при y+<7 расположен очень тонкий вязкий подслой, в котором течение определяется молекулярной вязкостью и распределение скорости выражается линейной зависимостью
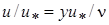 или
или 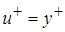 . (2.30)
. (2.30)
За вязким подслоем следует переходная зона, для которой, несмотря на существенные турбулентные пульсации, необходимо учитывать влияние вязкости. Далее, при y+>25 течение приобретает развитый турбулентный характер и распределение скоростей следует логарифмическому закону
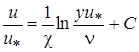 , (2.31)
, (2.31)
где c - универсальная постоянная порядка 0,4; С – постоянная, определяемая экспериментальным путем, С=5,5 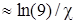 , поэтому формулу (2.31) можем записать в следующем виде:
, поэтому формулу (2.31) можем записать в следующем виде:
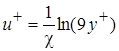 . (2.31а)
. (2.31а)
Поскольку величина 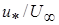 слабо меняется с Re, закон распределения осредненной скорости для плоской пластины может быть выражен зависимостью
слабо меняется с Re, закон распределения осредненной скорости для плоской пластины может быть выражен зависимостью 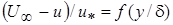 . (2.32)
. (2.32)
Ввиду некоторой неопределенности толщины пограничного слоя было предложено заменить безразмерное расстояние y/d безразмерным расстоянием 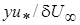 , которое включает в себя более точно определяемую толщину вытеснения
, которое включает в себя более точно определяемую толщину вытеснения 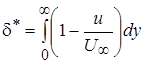 . (2.33)
. (2.33)
Важная качественная характеристика – толщина потери импульса
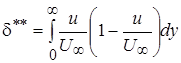 (2.34)
(2.34)
может быть представлена в виде 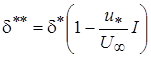 , (2.35)
, (2.35)
где 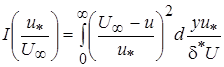 .
.
Основные принципы подобия подтверждаются универсальностью зависимости 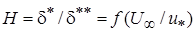 .
.
В дальнейшем под толщиной пограничного слоя d будем подразумевать расстояние от стенки, на котором значение скорости 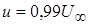 .
.
Переход от ламинарного течения к турбулентному характеризуется сильным ростом толщины пограничного слоя. Если в условиях ламинарного пограничного слоя [1,4]: 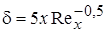 , (2.36)
, (2.36)
то для турбулентного пограничного слоя, согласно известному выражению Шлихтинга: 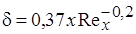 . (2.37)
. (2.37)
Аналогично образованию гидродинамического пограничного слоя над поверхностью, имеющей температуру, отличающуюся от температуры потока, образуется тепловой пограничный слой. Тепловой поток (при 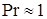 ), преодолев сопротивление вязкого подслоя, распространяется по всему пространству турбулентно движущейся жидкости в пограничном слое. Таким образом, толщины теплового и гидродинамического пограничных слоев совпадают. С увеличением числа Pr перепад температуры, приходящийся на вязкий подслой, становится все больше.
), преодолев сопротивление вязкого подслоя, распространяется по всему пространству турбулентно движущейся жидкости в пограничном слое. Таким образом, толщины теплового и гидродинамического пограничных слоев совпадают. С увеличением числа Pr перепад температуры, приходящийся на вязкий подслой, становится все больше.
Соображения, используемые для установления законов подобия в распределении скорости, могут быть применены и к распределению температуры. В таком случае в пристенной области распределение температур можно выразить законом подобия:
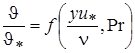 , (2.38)
, (2.38)
где 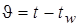 - разность температур жидкости и стенки,
- разность температур жидкости и стенки,
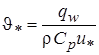 - характеристическая температура.
- характеристическая температура.
Для зоны вязкого подслоя 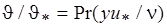 , (2.39)
, (2.39)
а для зоны логарифмического распределения
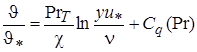 . (2.40)
. (2.40)
Во внешней области пограничного слоя распределение температуры следует закону изменения температуры: 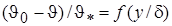 ,
,
где 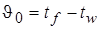 - разность температур потока и стенки. В этой области турбулентного течения изменение температуры не должен зависеть от Pr.
- разность температур потока и стенки. В этой области турбулентного течения изменение температуры не должен зависеть от Pr.
Указанные законы подобия с достаточно хорошим приближением подтверждаются в условиях автомодельного развития пограничного слоя.
При осреднении уравнений турбулентного пограничного слоя [3,9] возникают неизвестные функции турбулентных напряжений трения 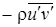 и потоков тепла
и потоков тепла 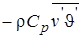 , отыскание связей которых со свойствами осредненного течения составляет основную проблему при решении задач турбулентного переноса. Теория турбулентности развивается, в основном, в двух направлениях. Первое направление связано с идеями Прандтля и Кармана о длине пути перемешивания, а во втором направлении, развитом на гипотезах А.Н. Колмогорова, для замыкания уравнений движения и энергии используются уравнения баланса пульсационных величин с привлечением гипотез относительно неизвестных членов, содержащихся в замыкающих уравнениях.
, отыскание связей которых со свойствами осредненного течения составляет основную проблему при решении задач турбулентного переноса. Теория турбулентности развивается, в основном, в двух направлениях. Первое направление связано с идеями Прандтля и Кармана о длине пути перемешивания, а во втором направлении, развитом на гипотезах А.Н. Колмогорова, для замыкания уравнений движения и энергии используются уравнения баланса пульсационных величин с привлечением гипотез относительно неизвестных членов, содержащихся в замыкающих уравнениях.
Модель пути смешения Прандтля
Основа модели Прандтля: плоское течение с направлением, одинаковым во всех точках пространства, и со скоростью, изменяющейся только при переходе от одной линии тока к другой. Пусть направление главного течения совпадает с осью х. Следовательно [9]: 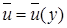 ,
, 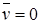 ,
, 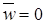 .
.
Такой случай осредненного течения осуществляется, например, при течении в прямоугольном канале. Из касательных составляющих тензора напряжений в рассматриваемом случае имеется только касательное напряжение 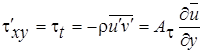 . (2.41)
. (2.41)
Механизм турбулентного течения можно представить в виде следующей упрощенной картины.
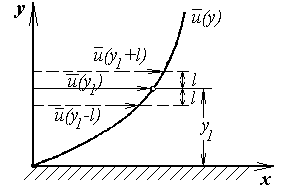
Рис. 2.3.Модель Прандтля
В турбулентном течении возникают жидкие объемы, каждый из которых обладает собственной скоростью и движется на протяжении некоторого расстояния как в продольном, так и в поперечном направлении в виде неразрывного целого с сохранением составляющей своего импульса. Предположим, что один такой жидкий объем, возникший в слое (y1- l) и обладающий скоростью u(y1- l), перемещается на расстояние l в направлении, перпендикулярном к главному течению (рис. 2.3). Назовем расстояние l путем перемешивания. Если рассматриваемый жидкий объем сохраняет x-составляющую своего импульса, то в новом слое он будет иметь меньшую скорость, чем окружающая его новая среда. Разность между новой и старой скоростями 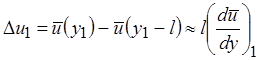 . (2.42)
. (2.42)
Последнее выражение получается в результате разложения скорости u(y1-l) в ряд Тейлора. При таком поперечном течении v' > 0. Аналогичным образом жидкий объем, попадающий в слой y1 из слоя y1+ l, имеет в новом месте большую скорость, чем окружающая его там среда. Разность скоростей
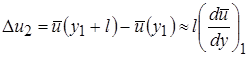 , (2.43)
, (2.43)
причем теперь v' < 0. Каждую из разностей скоростей 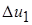 и
и 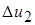 , вызванных поперечным движением, можно понимать как турбулентную пульсацию скорости в слое y1. Следовательно, осредненное во времени значение абсолютной величины этой пульсации
, вызванных поперечным движением, можно понимать как турбулентную пульсацию скорости в слое y1. Следовательно, осредненное во времени значение абсолютной величины этой пульсации
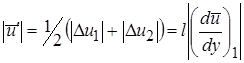 . (2.44)
. (2.44)
Это соотношение позволяет дать пути перемешивания l следующее физическое толкование: путь перемешивания представляет собой то расстояние в поперечном направлении течения, которое частица жидкости, двигаясь со средней скоростью своего первоначального слоя, должна пройти для того, чтобы разность ее скорости и скорости течения в новом месте стала равной осредненному значению абсолютной величины продольной пульсации турбулентного течения.
Величина поперечной скорости v' имеет такой же порядок, как и величина продольной скорости u', и поэтому мы можем написать, что
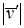 = число-
= число- 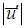 = число
= число 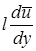 . (2.45)
. (2.45)
Изложенное выше приводит к следующему выводу. Частицы жидкости, приходящие в слой y1 с положительным значением v' (рис. 2.3 - снизу), вызывают «обычно» отрицательную пульсацию u', поэтому для таких частиц произведение u'v' отрицательно. Частицы же жидкости, приходящие в слой y1 с отрицательным значением v' (сверху), вызывают «обычно» положительную пульсацию u', следовательно, для них произведение u'v' также отрицательно. Говоря об «обычно» положительных или «обычно» отрицательных пульсациях, не исключают возможность возникновения пульсации с противоположным знаком, но количество таких пульсаций может быть только очень небольшим. Таким образом, осредненное во времени значение u'v' отличается от нуля, и притом отрицательно. Поэтому можем принять, что
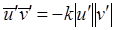 , (2.46)
, (2.46)
где коэффициент k, совпадает с коэффициентом корреляции. Заменяя 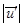 и
и 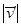
 их выражениями, получим:
их выражениями, получим: 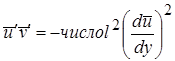 . (2.47)
. (2.47)
«Число» в этом соотношении не совпадает с «числом» в соотношении (2.45), так как включает коэффициент k из равенства (2.46). Если, включить это новое «число» в пока еще неизвестную длину пути перемешивания l, то
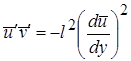 . (2.48)
. (2.48)
Внеся это значение 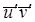 в формулу (2.41) для турбулентного касательного напряжения, получим:
в формулу (2.41) для турбулентного касательного напряжения, получим: 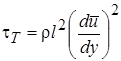 . (2.49)
. (2.49)
Правильнее придать этой формуле следующий вид:
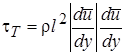 , (2.50)
, (2.50)
так как очевидно, что при изменении знака производной 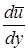 должен меняться знак и касательного напряжения.
должен меняться знак и касательного напряжения.
Из сопоставления формул следует, что коэффициент турбулентного трения равен: 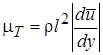 или
или 
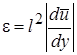 , (2.51)
, (2.51)
где 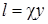 ,
, 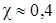 . Это дает возможность в уравнении (2.26) рассчитать величину
. Это дает возможность в уравнении (2.26) рассчитать величину 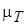 . Из модели Прандтля (2.50) следует логарифмический профиль скорости в турбулентном ядре:
. Из модели Прандтля (2.50) следует логарифмический профиль скорости в турбулентном ядре:
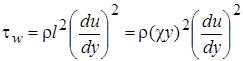 ,
, 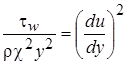 ,
,
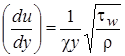 ,
, 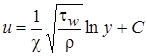 ,
,
так как 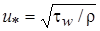 , то получим выражение (2.31).
, то получим выражение (2.31).
Формула Прандтля (2.50) с успехом применяется для расчета турбулентных течений вдоль стенок (в трубе, в канале, вдоль пластины), а также для расчета так называемой свободной турбулентности, т. е. таких турбулентных течений, которые не ограничены стенками.
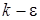 модель турбулентности
модель турбулентности
Для ряда задач достаточно хорошие результаты дает k-eмодель турбулентности. Основным является допущение о том, что свойства турбулентности можно адекватно охарактеризовать двумя величинами: 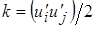 - кинетической энергией турбулентных пульсаций и
- кинетической энергией турбулентных пульсаций и 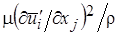 - скоростью диссипации этой энергии.
- скоростью диссипации этой энергии.
Хотя общеизвестно, что это является крайне сильным упрощением действительного, чрезвычайно сложного механизма турбулентного движения, но при таком подходе учитываются его существенные стороны в той степени, которая необходима для создания полезной основы расчётов.
Конечно, само по себе введение в анализ величин k и eне устраняет трудностей определения свойств турбулентного переноса. Необходимо иметь средства расчёта этих параметров. В аппарате турбулентного моделирования k и e рассматриваются как удовлетворяющие транспортным уравнениям, во многом подобным тем, которые управляют переносами импульса и энергии.
Ниже показано транспортное уравнение для турбулентной энергии, во многих аспектах оно подобно уравнению переноса для энтальпии (1.7). В частности, конвективные, нестационарные члены в левой части и диффузионные - в правой полностью идентичны. Диффузионный коэффициент турбулентной энергии по величине предполагается подобным коэффициенту эффективной вязкости:
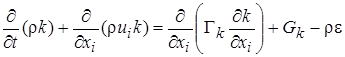 . (2.52)
. (2.52)
Однако уравнение для k отличается от уравнения для h присутствием добавочных членов в конце правой части. Первый из этих членов 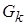 - довольно громоздкая функция турбулентной вязкости и определённых градиентов скорости. Он выражает интенсивность порождения турбулентности в единице объёма за счёт сдвиговых напряжений и градиентов скорости:
- довольно громоздкая функция турбулентной вязкости и определённых градиентов скорости. Он выражает интенсивность порождения турбулентности в единице объёма за счёт сдвиговых напряжений и градиентов скорости: 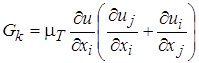 . (2.53)
. (2.53)
Второй член 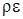 представляет скорость диссипации энергии турбулентности в единице объёма.
представляет скорость диссипации энергии турбулентности в единице объёма.
Турбулентная вязкость, которая для течений с высокими числами Рейнольдса эквивалентна эффективному значению, связывается с турбулентной энергией и диссипацией простой функцией, форму которой можно получить из анализа размерностей. Константа 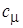 предполагается универсальной:
предполагается универсальной:
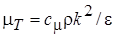 , а
, а 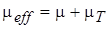 . (2.54)
. (2.54)
Заметим, что существуют и такие версии этой модели турбулентности, которые описывают области потоков с низкими числам Рейнольдса. В этом случае эмпирические константы заменяются функциями местных чисел Re турбулентности 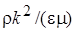 , где m - молекулярная вязкость.
, где m - молекулярная вязкость.
Нужно подчеркнуть, что уравнение (2.52) частично получается из прямого преобразования уравнений турбулентного движения, а частично основано на ряде интуитивных предположений о моделировании его отдельных членов. Сама идея о том, что турбулентная энергия по существу может вести себя как концентрация химической компоненты, т.е. переноситься конвекцией и диффузией, производиться и исчезать, впервые была высказана Колмогоровым на основе чисто феноменологических рассуждений.
Уравнение, которое описывает диссипацию турбулентной энергии, имеет следующий вид:
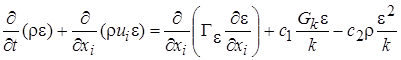 . (2.55)
. (2.55)
Оно очень близко к уравнению для переноса k (2.52). Однако источниковый и стоковый члены в правой части содержат две добавочные константы 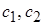 . Предполагается, что они также имеют универсальные значения, которые могут быть получены из некоторых экспериментов и затем остаются пригодными и для других.
. Предполагается, что они также имеют универсальные значения, которые могут быть получены из некоторых экспериментов и затем остаются пригодными и для других.
Численные значения констант, которые можно рекомендовать для расчётов, указаны в табл. 1, включая три числа Прандтля: для энергии турбулентности, температуры, диссипации. Как видим, все они имеют значения, близкие к единице.
Таблица 1
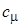
| 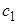
| 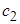
| 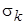
| 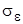
| 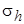
|
| 0,09 | 1,44 | 1,92 | 1,0 | 1,3 | 0,9 |
В настоящее время существуют только два способа учёта закономерностей пристенных областей в численных расчётах турбулентных течений: метод пристенных функций и специальные модификации в математической модели турбулентности для её использования в окрестности стенок. В расчётах наиболее часто применяется первый подход, в основном, из-за соображений экономии компьютерной памяти и времени вычислений.
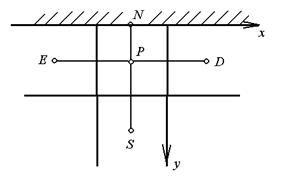 Рис. 2.4.Расположение пристеночных узлов Рис. 2.4.Расположение пристеночных узлов
| 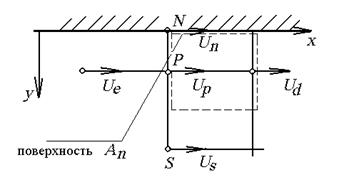 Рис. 2.5.Численная реализация граничного условия для U Рис. 2.5.Численная реализация граничного условия для U
|
Рассмотрим узловые точки N и P конечно-разностной схемы (рис. 2.4). Необходимым условием использования пристенных функций является достаточное удаление узла P от N, для того чтобы первый попал в область турбулентного ядра пограничного слоя.
Предполагается, что изменение скорости в пристенной области определяется логарифмическим законом (2.31) :
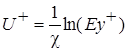 , (2.56)
, (2.56)
где 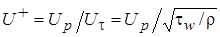 , и
, и 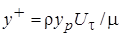 . (2.57)
. (2.57)
Константы E и c полагаются универсальными со значениями: Е=9,0 и c=0,4.
Скорость трения 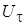 и динамическая безразмерная координата
и динамическая безразмерная координата 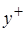 соотносятся друг с другом при помощи функциональной связи, которую можно получить из решения уравнения переноса для кинетической энергии турбулентности при отсутствии влияния конвекции и диффузии. Эти условия реализуются в ядре турбулентного пограничного слоя, где выполняется баланс между порождением и диссипацией турбулентных пульсаций.
соотносятся друг с другом при помощи функциональной связи, которую можно получить из решения уравнения переноса для кинетической энергии турбулентности при отсутствии влияния конвекции и диффузии. Эти условия реализуются в ядре турбулентного пограничного слоя, где выполняется баланс между порождением и диссипацией турбулентных пульсаций.
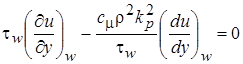 , (2.58)
, (2.58)
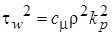 ,
, 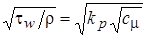 ,
,
где 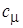 определяется из экспериментальных данных,
определяется из экспериментальных данных, 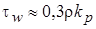 ,
, 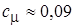 .
.
Результат такого решения  , (2.59)
, (2.59)
и 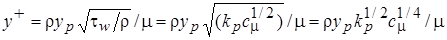 . (2.60)
. (2.60)
Подставляя (2.59) и (2.60) в (2.56), получаем функцию стенки для скорости:
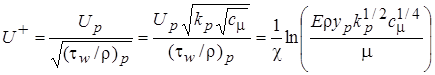 . (2.61)
. (2.61)
Отсюда можно получить выражение для вычисления трения на стенке (предполагается, что между точками N и P оно не меняется):
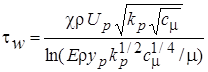 . (2.62)
. (2.62)
Это соотношение используется как граничное условие для скорости U на стенке (рис. 2.5) при использовании 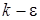 модели.
модели.
Эффект 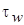 выражается в каждом пристенном контрольном объёме путём:
выражается в каждом пристенном контрольном объёме путём:
1) разрыва связей узлов со стенкой при 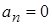 ;
;
2) включением 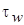 в уравнение баланса для
в уравнение баланса для 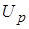 через дополнительный источниковый член
через дополнительный источниковый член 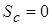 ,
, 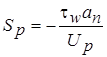 .
.
Скорость диссипации энергии e близи стенки определяется предположением о линейности изменения длины пути смешения от расстояния до стенки: 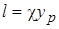 .
.
Это допущение приводит к следующему соотношению:
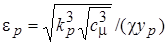 , (2.63)
, (2.63)
которое и выступает как граничное условие для e-уравнения. Наиболее удобно его включить в вычисления через источниковый член уравнения баланса e для пристенного контрольного объёма 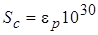 и
и 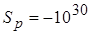 .
.
Величина 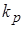 рассчитывается из обычного балансового уравнения для k, но с учётом следующих его модификаций в пристенной области: отсутствия диффузионного переноса кинетической энергии и включения напряжения трения на стенке в источник k. Член диссипации также модифицируется как осреднённая по пристенному контрольному объёму величина:
рассчитывается из обычного балансового уравнения для k, но с учётом следующих его модификаций в пристенной области: отсутствия диффузионного переноса кинетической энергии и включения напряжения трения на стенке в источник k. Член диссипации также модифицируется как осреднённая по пристенному контрольному объёму величина:
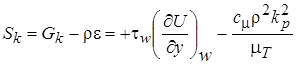 , (2.64)
, (2.64)
или 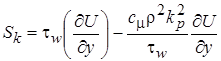 .
.
Тепловые (концентрационные) граничные условия также устанавливаются по известным пристенным законам, связывающим поток теплоты (массы) у стенки с величиной трения:
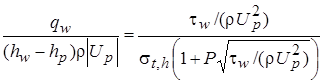 , (2.65)
, (2.65)
где 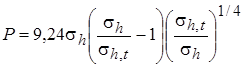 . (2.66)
. (2.66)
Обозначим через SKIN и STAN (пристенные функции):
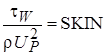 ,
, 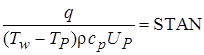 .
.
Тогда мы получим следующее выражение:
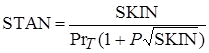 , (2.65а)
, (2.65а)
где в соответствии с уравнением (2.66) коэффициент P
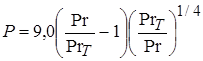 . При Pr=1 STAN=SKIN.
. При Pr=1 STAN=SKIN.
Если необходимо получить значение температуры на стенке или коэффициента теплоотдачи, можно воспользоваться следующими выражениями (считая т.P – 1 КО): 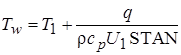 .
.
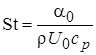 ;
; 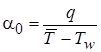 ;
;
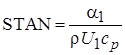 ;
; 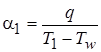 ;
; 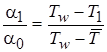 .
.
Значение Стантона можно записать как 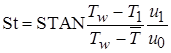 ;
;
значение числа Нуссельта
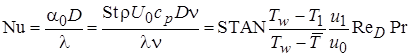 , (2.67)
, (2.67)
где D - характерный размер, 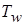 - температура на стенке,
- температура на стенке, 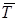 - среднемассовая температура, i=1 - первый контрольный объём.
- среднемассовая температура, i=1 - первый контрольный объём.
Запишем уравнение (2.62) через пристенные функции, в виде:
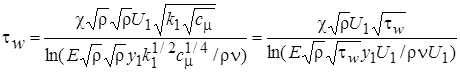 ,
,
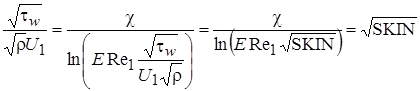 ,
,
где Е=9,0, c=0,41. Для турбулентного течения
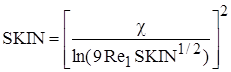 , при
, при 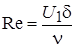 . (2.68)
. (2.68)
Коэффициент трения: 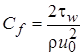 ;
; 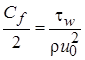 ;
; 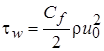 .
.
Перепишем через пристенные функции, тогда  ,
,
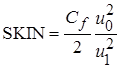 ,
, 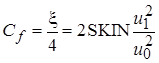 ,
, 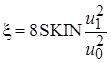 .
.
Определение гидродинамического сопротивления и теплоотдачи является конечной и основной задачей при рассмотрении конвективного переноса в теплообменнике.
Дата добавления: 2020-10-25; просмотров: 1130;











