Характеристика шкал
| Наименование шкал (классификация по виду допустимых преобразований j) | Допустимые преобразования j | Допустимые действия | Статистики на шкалах | Примеры исследования | ||
 
Направление возможного перевода шкалы
| Нечисловые (неметрические шкалы) | Номинальные (назывные, наименований, классификации) | ∞ – эквивалентность (различия) шкала, единственная до однозначного преобразования | Операции логического сравнения (над текстами) | Частоты, распределение частот, средняя тенденция | Для однозначной идентификации объекта, классификации документов, функций, подразделений и т.д. |
| Порядковая (ранговая, интенсивности) | 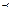 порядка
шкала, единственная до монотонного преобразования
| Операции логического сравнения и возведение в степень, извлечение корня | Ранговые статистики, ранговая корреляция по Спирмену и Кенделу | Для упорядочения объектов временная шкала, шкала твердости минералов Мосса, иерархия уровней, баллы | ||
| Числовые (количественные, метрические) шкалы | Интервалов |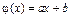 
шкала, единственная с точностью до линейного преобразования (х – значение числа)
| Операции сложения, умножения, деления (все операции над действительными числами) | Все методы классической математической статистики. Коэффициент парной корреляции Пирсона | Различие между свойствами объектов (шкалы температур, полезности). имеется точка отсчета и масштаб | |
| Частные случаи шкалы интервалов | Отношений | j(х) = ах частный случай шкалы интервалов при выборе нулевой точки | - « - | Свойства объекта – мас-сы, длины, веса (во сколько раз) | ||
| Разностей | j(х) = х + b частный случай шкалы интервалов при выборе единичного масштаба | - « - | Свойства объекта (на сколько больше или меньше) | |||
| Абсолютная | j(х) = х частный случай шкалы интервалов для нулевой точки и единичного масштаба. Шкала единственная до тождественного преобразования | - « - | Для определения количества объектов единственным образом с помощью натуральных чисел |
Т а б л и ц а 1.19
Дата добавления: 2020-10-25; просмотров: 344;
Поиск по сайту
Узнать еще
- Cодержание субшкальных диагностических концептов
- I. Общая характеристика категории состояния как часть речи
- II. Лексико-грамматические разряды имен числительных. Их характеристика.
- II. Лексико-грамматические разряды местоимений. Их общая характеристика
- II. Шкала порядка (шкала рангов)
- III. Шкала интервалов (разностей)
- IV. ОБЩАЯ ХАРАКТЕРИСТИКА ВИРУСОВ
- U - образная характеристика
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
