Определение абсолютной значимости функции
| Идентификатор функции | Идентификатор функции | Количество предпочтений | Значимость функций | |||
| F1 | F2 | F3 | F4 | |||
| F1 | F1 | F1 | F1 | 3/6 | ||
| F2 | F1 | F2 | F2 | 2/6 | ||
| F3 | F1 | F2 | F4 | |||
| F4 | F1 | F2 | F4 | 1/6 | ||
| Итого |
При определении значимости функций в графе 7 табл. 1.13 необходимо выполнять нормирующее условие: равенство единице суммы абсолютных значимостей вершин, исходящих из одной и той же вершины. В целом, для всей ФМ нормирующее условие можно записать в виде правила: 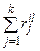 =1, где
=1, где 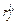 – вес (значимость) узла ФМ, l – номер узла на i-м уровне иерархии, j – номер функции в l-м узле i-го уровня ФМ, j = 1…k.
– вес (значимость) узла ФМ, l – номер узла на i-м уровне иерархии, j – номер функции в l-м узле i-го уровня ФМ, j = 1…k.
Найденная абсолютная значимость функции j для l-го узла дерева на i-м уровне иерархии позволяет определить ее относительную важность для объекта в целом. Относительную важность любой функции для объекта в целом можно определить из соотношения
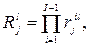 где i = 1…, I; I – количество уровней иерархии ФМ, функция
где i = 1…, I; I – количество уровней иерархии ФМ, функция 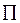 – произведение абсолютных значимостей по любой (а в целом для ФМ по каждой) ветке дерева ФМ.
– произведение абсолютных значимостей по любой (а в целом для ФМ по каждой) ветке дерева ФМ.
Полученные относительные значения важности каждой функции в ФМ позволяют осуществить функционально-стоимостную диагностику объекта в целом и определить степень соответствия между затратами и относительной важностью и полезностью функций, т. е. выявить технико-экономический дисбаланс и наличие противоречий исследуемого или вновь проектируемого объекта.
Метод расстановки приоритетов. Этот метод (МРП), как и метод МПС, является методом экспертного оценивания, позволяющим получить количественную оценку качественного признака. Однако его используют в случаях, когда нельзя выявить явное предпочтение одного варианта перед другим.
Схема работы МРП. Имеется некоторый критерий k, в соответствии с которым необходимо расставить приоритеты исследуемых вариантов или функций fi, i = 1…n. Пусть n = 4, тогда мы имеем 4 функции для упорядочения по критерию k: f1, f2, f3, f4.
Строится матрица для сравнения функций (табл. 1.14).
Т а б л и ц а 1.14
Дата добавления: 2020-10-25; просмотров: 476;











