Определение приоритетов функций

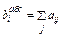
I	j	Абсолютный приоритет	Относительный приоритет
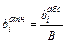
f1	f2	f3	f4
f1		0,5		0,5		3/16 = 0,19
f2	1,5		1,5	0,5	4,5	4,5/16 = 0,28
f3		0,5		0,5		3/16 = 0,19
f4	1,5	1,5	1,5		5,5	5,5/16 = 0,34

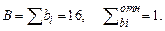
Метод решающих матриц Г.С. Поспелова (1960-е гг.). Впервые он был применен для анализа проблемы распределения ассигнований на фундаментальные исследования. При проведении ФСА метод может быть использован для определения значимости функции в случае, если невозможно получить ФМ объекта строго иерархической структуры. Иногда ФМ можно представить только матричной структурой (табл. 1.16), например, в случае анализа матричных организационных структур.

Т а б л и ц а 1.16

Определение значимости функций для матричной ФМ

			Задачи (цели)
			а1	а2	aj …	am	J = 1…m
	Функции b	b1 i = 1...n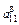
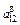
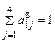
	b2					. . .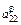
	bi			. . .	. . .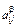
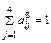
	b4
	bn
			a1	a2	aj	am
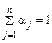		– взвешивание целей (условие нормализации),   aj – вес задачи

По каждой строке необходимо найти вклад каждой функции в достижение j-й цели, нормируя его: 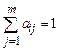. Теперь можно найти вес каждой функции в общей структуре ФМ: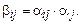

Элементы теории измерений

Основные понятия Шкалы измерений

«Наука начинается с тех пор, как начинают измерять», – эти знаменитые слова Д.И. Менделеева ясно определяют необходимость измерений.

При анализе сложных экономических информационных систем исследователи и проектировщики выходят за границы привычного теоретико-множественного подхода к описанию объектов и вынуждены использовать системный подход (логико-методологическую концепцию) как альтернативу традиционным методам эконометрики. Однако необходимость в измерениях объясняется тем, что аналитики для строгости и рациональности обоснования своих выводов используют теоретико-множественную математику как привычный всем язык доказательств, так как недостаток ощутимой, измеримой информации приводит к безличности логики и прямой потере строгости. Чтобы вообще что-нибудь определенное сказать о системах, необходимо владеть теоретико-множественным аппаратом во всей его строгости и математической мощи [8].

Аналитики изучают наблюдаемый объект, осуществляют его первоначальное, формальное описание и вводят необходимые измерители свойств, отношений, признаков и т.д.

Для формального описания системы как множества объектов и отношений между ними вводится понятие эмпирической системы с отношениями [8].

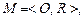где М – система, 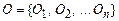– множество объектов (предметов, явлений, событий, решений и т. д.), 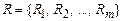– множество отношений между объектами. Запись 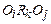означает, что объект О_i находится в отношении R_k к объекту О_j. Отношение называется двухместным, если оно связывает два объекта; если оно связывает три объекта, оно называется трехместным и т.д.

Основные свойства отношений. Отношение R рефлексивно, если 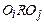истинно. Отношение R антирефлексивно, если 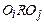ложно. Отношение R симметрично, если из 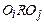следует 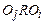. Отношение R антисимметрично, если из 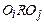и 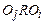следует 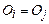. Отношение R несимметрично, если из истинности 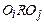следует, что 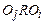ложно. Отношение R транзитивно, если из 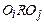и 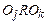следует 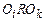, где 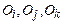суть элементы множества О. Отношение, которое обладает свойствами рефлексивности, симметричности и транзитивности называется отношением эквивалентности .

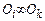Отношение порядка О_i предпочтительнее О_j, обозначается 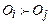. Оно обладает свойствами антирефлексивности и транзитивности (оно означает, например, «больше чем», «раньше чем», «предпочтительнее чем»).

Разнообразие возможных объектов и видов отношений в наблюдаемых реальных системах привело к необходимости введения универсальной системы с отношениями. В качестве такой системы используют числовую систему 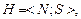где N – множество действительных чисел; 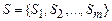– множество отношений между числами.

Основными проблемами теории измерений являются проблемы представления и единственности. Проблема представления заключается в доказательстве того, что для наблюдаемой системы 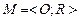можно построить подобную числовую систему 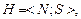такую, чтобы она была изоморфной, или, по крайней мере, гомоморфной наблюдаемой системе.

Подобными называются две системы 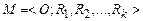и 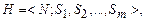если число отношений в них одинаково:
k = m и местность отношений одинакова (например, 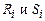– двухместные отношения).

Числовая система 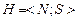изоморфна эмпирической системе 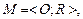если эти системы подобны и существует взаимно однозначное отображение (функция) f между системами. Это означает, что любые изменения в системе Н должны быть учтены в системе М и наоборот, любые изменения в системе М должны быть учтены в системе Н.

Условие взаимной однозначности отображения является слишком жестким и не всегда необходимым. Поэтому чаще используют условие гомоморфности отображения. Числовая система 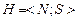гомоморфна эмпирической системе 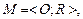если эти системы подобны и существует однозначное отображение системы М в Н.

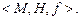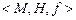Проблему единственности можно сформулировать как проблему определения типа шкалы. Шкалой называется совокупность эмпирической и числовой систем и отображения, т. е. Пусть и 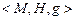– две шкалы с разными отображениями f и g, тогда возникает вопрос о взаимосвязи числовых значений, полученных этими отображениями, например, 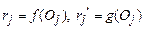. Связь между числами 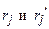запишем с помощью функци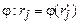и или 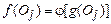. Функция 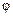называется допустимым преобразованием шкалы. Смысл этого определения состоит в том, что свойства функции 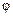устанавливают связи между всеми числовыми системами, выбираемыми для описания эмпирической системы. Свойства функции 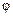определяют тип шкалы и позволяют классифицировать шкалы измерения по виду допустимого преобразования 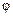. Описание типов шкал удобно представить в виде таблицы (табл. 1.18). Правильное использование методов обработки данных определяется типом данных. Исследователь (эксперт) должен работать в тесном контакте с математиками при выборе методов обработки экспертной информации.

Построение шкал измерений – ответственный и трудоемкий процесс [10]. Прежде всего, необходимо оценить надежность шкалы. Содержание деятельности по проверке надежности шкал характеризуется табл. 1.19.

Т а б л и ц а 1.18