Определение медианы

<6 7 8910 11 12 >

Медиана(Me)– средняя, относительно которой ряд распределения делится на 2 половины (в обе стороны от медианы) одинаковое количество вариант.

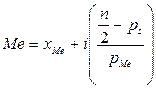где: X_Me – нижняя граница интервала, в котором находится Ме или полусумма соседних классовых вариант; i – величина классового интервала; n – объем выборки; p_s – число накопленных частот, стоящее перед медианным классом; p_Me – частота медианного класса.

´Задача 2.16[5]. (см. Задачу 2.4) Вычислить Ме ряда распределения Са (мг%) в сыворотке крови павианов гамадрилов

Классы по содержанию Са в сыворотке крови	Срединные значения классов	Частоты (p_i)	Накопленные частоты (p_s)
8,6 – 9,3	9,0
9,4 – 10,1	9,8
10,2 – 10,9	10,6
11,0 – 11,7	11,4
11,8 – 12,5	12,2
12,6 – 13,3	13,0
13,4 – 14,1	13,8
14,2 – 14,9	14,6

Вариант 1.i = 0,8.Величина n/2= 50находится между p_s = 46 и p_s = 71.

Границы интервала для (p_s = 71) – 11,8 ÷ 12,5 т. е. p_Me = 25.

По формуле: Ме = 11,8 + 0,8 (50 – 46) / 25 = 11,93.

Вариант 2.По формуле: Ме = (11,4 + 12,2) / 2 + 0,8 (50 – 46)/25 = 11,93.

´Задача 2.17[5](см. задачу 2.6). Вычислить Ме ряда распределения численности поросят.

Классы (x_i)	Частоты (p_i)	Накопленные частоты	Величина n/2= 32находится между p_s = 24 и p_s = 39. То x_Me = (7+8)/2 = 7,5; p_Me = 15. По формуле: Ме = 7,5 + 1 (32 – 24)/15 = 7,5 + 0,53 = 8,03.








	Σp_i= 64

Определение моды

Мода(Mo)– наиболее часто встречающаяся, в данной выборке, величина. Класс с наибольшей частотой называется модальным.

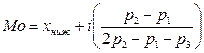где: X_ниж – нижняя граница модального класса; i – величина классового интервала; p₁ – частота класса, предшествующего модальному; p₂– частота модального класса; p₃ – частота класса, следующего за модальным.

´Задача 2.18[5](см. задачу 2.4). Вычислить (используя MS Excel) Мо ряда распределения Са (мг%) в сыворотке крови павианов гамадрилов. i = 0,8. По формуле Мо = 11,8 +0,8 (25-23) / (2×25-23-17) = 11,8+0,16 = 11,96.	Классы по содержанию Са в сыворотке крови	Срединные значения классов	Частоты (p_i)	Накопленные частоты (p_s)
8,6 – 9,3	9,0
9,4 – 10,1	9,8
10,2 – 10,9	10,6
11,0 – 11,7	11,4
11,8 – 12,5	12,2
12,6 – 13,3	13,0
13,4 – 14,1	13,8
14,2 – 14,9	14,6

Хи-квадрат

Хи-квадрат (χ²) – это непараметрический статистический показатель, используемый для определения того, отличается ли наблюдаемая частота результатов от ожидаемой частоты. Поскольку для подсчета χ² необходимы частоты, можно использовать как количественные, так и качественные переменные. Формула для χ², где О соответствует наблюдаемой (эмпирической) частоте, а Е – ожидаемой (теоретической):

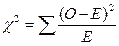Степени свободы df для χ², где R – число строк, а С – число столбцов в таблице распределения частот, находят с помощью формулы .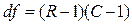

´Задача 2.19 [9]. Наблюдается ли различие между уровнем знаний женщин и мужчин? При вычислении χ² желательно пользоваться таблицами распределения частот, помогающими упорядочить О и Е частоты. В таблице распределения эмпирических частот подсчитываются суммы по столбцам, по строкам и общая сумма n. Чтобы подсчитать значение для каждой клетки в таблице распределения теоретических частот, умножьте сумму всей строки на сумму столбца и разделите полученный результат на общую сумму n. Затем эти величины О и Е используются в формуле для вычисления критерия хи-квадрат

Таблица распределения эмпирических частот (O)

Пол	Низкий	Высокий	Итого
Женщины
Мужчины
Итого			п = 17

Таблица распределения теоретических частот (E)

Пол	Низкий	Высокий	Итого
Женщины	(9×8)/17 = 4,24	(9×9)/17 = 4,76
Мужчины	(8×8)/17 = 3,76	(8×9)/17 = 4,24
Итого			п = 17

Х2	Х9
категория	Уровень знаний	O	Е	(O – Е)	(O – Е)²	(O – Е)²/Е
Женщины	Низкий		4,24	1,76	3,11	0,74
	Высокий		4,76	– 1,76	3,11	0,65
Мужчины	Низкий		3,76	– 1,76	3,11	0,83
	Высокий		4,24	1,76	3,11	0,74

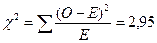В нашем примере R = 2 и С = 2; таким образом, df = 1. Чтобы определить, превышает ли полученная нами величина χ² (2,95) желаемое критическое значение, мы обращаемся к табл. П 3.З. Критическое значение при df = 1 и уровне значимости 0,05 равно 3,84. Полученная нами величина 2,94 меньше этого критического значения; следовательно, между мужчинами и женщинами отсутствует статистически значимое различие в уровне знаний.