С БОЛЬШИМИ ОБЪЕМАМИ ВЫБОРОК

ЭКСПЕРИМЕНТАЛЬНЫЕ ПЛАНЫ С МАЛЫМИ ОБЪЕМАМИ ВЫБОРОК

Исследование, базирующееся на одиночном испытуемом или малой выборке, называется планом с малым n, или малым числом испытуемых. Большинство исследований в психологии базируется на большой совокупности испытуемых, которая позволяет получить большое количество данных. Соответствующие им планы экспериментов иногда называют планами с большим n [9].

Данные, полученные в ходе этих экспериментов, подлежат статистическому анализу, в котором могут быть сделаны вероятностные заключения и широкие обобщения. В силу огромной популярности экспериментов с большим n и их сопоставимости с современными статистическими приемами может показаться, что планы с малым n с методологической точки зрения второстепенны. Однако в таких отраслях наук о человеке, какклинические исследования, психофизика, оперантное научениеи спорт высших достижений,проведение экспериментальных планов с большими n зачастую оказывается просто невозможным.

Исследования, проводимые на одном испытуемом, связаны с особыми проблемами. В этих экспериментах измерения производятся до и после введения независимой переменной, а это означает, что сравнения производятся в различные периоды времени. В начальный период проводятся измерения с тем, чтобы определить исходный уровень (или базис), например, поведенческих характеристик, которые существуют до введения независимой переменной. Эти поведенческие характеристики можно измерить с помощью тестов, которые оценивают несколько черт поведения. Если исследователя интересуют эмоциональные изменения, которые происходят после введения независимой переменной, например, после введения в организм лекарства, меняющего настроение, базис может включать в себя описание нескольких характеристик, таких как ощущение счастья, непосредственность и общительность. После введения независимой переменной, в данном случае лекарства, меняющего настроение, производятся последующие оценки по тем же самым многомерным характеристикам. Эти показания сравниваются с исходным уровнем и представляют собой главный эффект исследования.

Клиническая психология. Поскольку в исследованиях с одним испытуемым решающую роль играют индивидуальные различия, необходимо подробное описание испытуемого. В исследованиях в области психотерапии это описание включает в себя «историю болезни», пример которой приведен в прил. 1. Автор эксперимента Реймонд Новако [9] дает описание клинических данных испытуемого, которые включают в себя описание его производственной ситуации, симптомы, госпитализацию, реакцию на стрессовые ситуации и предыдущее лечение. В клинических исследованиях идентификация этих характеристик особенно важна, так как именно определяют методику дальнейшего лечения.

Психофизические исследования. В психофизических экспериментах, как правило, изучается связь между физическими стимулами и тем, как испытуемый воспринимает эти стимулы. Во многих психофизических экспериментальных моделях каждый испытуемый подвергается воздействию десятков или даже сотен различных стимулов во время одного эксперимента. Тем самым, хотя количество наблюдений в психофизических экспериментах и базируется всего лишь на нескольких испытуемых (или даже на одном испытуемом), оно может превышать количество наблюдений в эксперименте с большим n. Кроме того, во многих психофизических экспериментах испытуемые не догадываются о возможном результате эксперимента. Фактически многие исследователи в этой области сами берут на себя роль испытуемых в собственных экспериментах, мотивируя это тем, что реакции испытуемого имеют физический характер и на них не влияет знание теории или гипотезы. Этот аргумент станет еще более основательным, если принять во внимание то, через какое большое количество опытов проходит каждый испытуемый.

Сюда же можно отнести и психофизиологические тесты.

Спорт высших достижений. Не секрет, что существуют «одиночные» виды спорта. Здесь ставка делается на одного или несколько спортсменов, которых обслуживает целая команда специалистов: тренеры, врачи, психологи и др. Функциональное, психическое и профессиональное состояние спортсмена – залог победы государства на международных соревнованиях. Проигрыш спортсмена обходится слишком дорого. По его выступлению судят не только о спортивных достижениях в стране, но, порой, и о самой стране. Поэтому в спортивной науке провести экспериментальный план с большим n зачастую просто невозможно. Спортсмена исследуют большим количеством тестов с применением информационных технологий [3] и компьютерных методов обработки данных.

Оперантное обусловливание. В начале XX в. в исследовательской деятельности психологов, специализировавшихся в области научения, доминировали две модели научения. Одна из них была разработана И.П. Павловым и называется классическим обусловливанием; вторая была предложена Э.Л. Торндайком, усовершенствована Б.Ф. Скиннером и носит название оперантного обусловливания. Начальные эксперименты в обоих направлениях исследований ставили целью идентифицировать необходимые для научения условия, используя подопытных животных. Павлов прибегал к помощи своих знаменитых выделявших слюну собак, а Торндайк исследовал, как эффект вознаграждения отражается на поведении кошек. Скиннер в своих экспериментах сначала использовал крыс, затем голубей и, наконец, наряду с различными видами животных, людей. Сейчас в лабораториях, где исследуются процессы научения, имеет место все более широкое использование различных видов животных для определения законов поведения.

Основу классического обусловливания, по Павлову, демонстрирует схема условного рефлекса. Известно, что проблему научения можно свести к выработке сложного комплекса условных рефлексов. Прежде чем приступать к изучению всего этого комплекса, необходимо рассмотреть простой одиночный условный рефлекс. Классический «слюнный» рефлекс можно описать следующим образом.

1. Когда собаке дают мясо (безусловный раздражитель), у нее выделяется слюна (безусловный рефлекс).

2. Звонит звонок, затем собаке дают мясо; это повторяют несколько раз.

3. Звонит звонок (условный раздражитель), у собаки выделяется слюна; условный рефлекс образовался.

4. Если условный раздражитель повторяется несколько раз, но собаке не дают мяса, она перестает реагировать на звонок; рефлекс угасает.

Алгоритм выработки условного рефлекса – это алгоритм высшего порядка, который изменяет, в соответствии с внешними условиями, алгоритм работы управляющей системы (системы безусловных и закрепившихся условных рефлексов). Выявление алгоритмов работы сложной управляющей системы, каковой является головной мозг, очень важно для понимания работы мозга.

Еще в 1958 г. отечественный исследователь А.А. Ляпунов указывал: «Критерием того, что функционирование некоторой управляющей системы изучено, является возможность моделировать ее...». Зная алгоритм выработки условного рефлекса, можно моделировать это явление на ПК или построить нервную сеть, поведение которой будет описываться этим алгоритмом. Последнее значительно интереснее, так как построенная нервная сеть позволит представить себе структуру и принципы строения нервных сетей, делающих возможным обучение и приспособление к окружающей обстановке, адаптацию.

Обозначим безусловный раздражитель буквой F, событие «появился безусловный раздражитель» – p(F); p(F) = 1, если безусловный раздражитель появился и p(F)=0, если он не появился. Условный раздражитель обозначим G, и р(G) – событие «появился условный раздражитель».

Имеется специальный математический аппарат для описания строения алгоритмов – логические схемы алгоритмов. Отдельные части алгоритма, перерабатывающего информацию, называются операторами. Будем обозначать их прописными латинскими буквами. В алгоритм могут входить некоторые логические условия, которыми определяется дальнейший порядок выполнения алгоритма. Будем обозначать логическое условие Р(Е). Так, в нашем алгоритме логическими условиями будут Р(G) и P(F). Логическое условие, например Р(G) будет выполнено, если появляется раздражитель G.

Алгоритм состоит из нескольких частей – операторов. Последовательное выполнение нескольких операторов будем обозначать как их произведение. Например, запись

A₁·A₂·A₃·A₄

означает, что сначала выполняется оператор A₁ , затем A₂ и т. д.

Выражение, составленное из операторов и логических условий, называется логической схемой алгоритма.

Например, логическая схема алгоритма безусловного рефлекса (F→a):

^1,2↓ K(F) P(F) ¹↑Aω ²↑

где: К(F) – оператор ввода информации;

А – оператор выполнения действия а, т. е. этот оператор заставляет систему совершить действие а;

ω – тождественно ложное условие, т. е. оно всегда не выполняется и поэтому всегда означает переход по стрелке;

Стрелки в этой схеме означают переход к следующей oneрации в случае невыполнения логического условия. Каждая стрелка имеет начало (стрелка вверх) и конец (стрелка вниз). Начало и конец отмечаются одинаковыми цифрами.

Для приведенного алгоритма, если Р(F)= 1, т. е. появился безусловный раздражитель, алгоритм выглядит так:

²↓ K(F) Aω ²↑

т. е. при появлении F система отвечает действием а и возвращается в исходное состояние по стрелке 2 (так как ω – тождественно ложное условие, т. е. оно всегда не выполняется и поэтому обозначает безусловный переход по стрелке).

Построим теперь логическую схему алгоритма выработки простого условного рефлекса. Пусть в системе имеется запоминающий элемент, который хранит возбуждение, связанное с событием GΛF (Λ – логический оператор «И»). Этот накопитель имеет порог h и, когда хранимое в нем возбуждение превзойдет порог h, образуется связь между условным раздражителем и действием (G→a). Обозначим текущее значение содержимого накопителя r и введем логическое условие р(r≥h) такое, что:

р (r ≥ h) = 1, если r ≥ h;

р (r ≥ h) = 0, если r < h.

Накопление возбуждения может происходить по различным законам (см. ниже).

Введем операторы: R – оператор накопления возбуждения в накопителе по определенному закону; S – оператор нейтрализации части возбуждения в накопителе; K(F,G) – оператор ввода информации.

Логическая схема алгоритма запишется в виде:

^3,4,7↓ K(F,G) p(G) ¹↑ p(F) ²↑ R ^5,6↓ Aω ³↑ ²↓ S p(r≥h) ⁴↑ ω ⁵↑ ¹↓ p(¯F) ⁶↑ ω ⁷↑

Такая запись алгоритма позволяет уже в некоторой степени представить, какова должна быть структура нервной сети. В этой нервной сети должны быть представлены события G, F, GΛF; эта нервная сеть должна иметь запоминающий элемент (накопитель) и какие-то переключающие элементы, управляемые накопителем. Все эти элементы должны быть соединены в соответствии с алгоритмом.

Задача построения нервной сети по заданному алгоритму имеет неоднозначное решение, можно построить различные сети, реализующие данный алгоритм в зависимости от того, какой элемент взять за основу нервной сети. В связи с этим возникает задача построения модели нейрона, более точно соответствующей реальному нейрону, что требует уточнения нейрофизиологических данных о нем.

Однако несмотря на неоднозначность решения, принципы построения нервной сети, реализующей данный алгоритм, и ее структура в общих чертах останутся одинаковыми для всех возможных сетей, поведение которых описывается данным алгоритмом.

Рассмотрим теперь нервную сеть, реализующую описанный алгоритм (алгоритм выработки классического условного рефлекса). На рис. 1.1 приведена схема нервной сети, предложенная Дж. Нейманом еще в 1956 г.

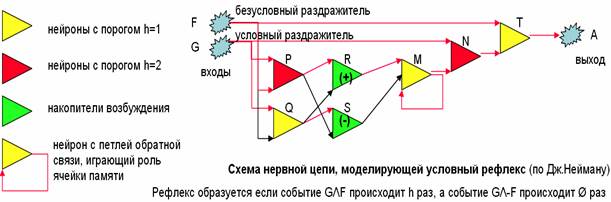
G – вход от условного раздражителя;

Рис. 1.1

F – вход от безусловного раздражителя;

А – выход;

Р, N – нейроны с порогом h = 2;

Q, М, T – нейроны с порогом h = 1;

R, S – накопители возбуждения

Сеть имеет два входа (G, F) и один выход (А). В необученном состоянии раздражитель G не вызывает никакой реакции (А = 0); возбуждение же рецептора F вызывает реакцию А, что иллюстрирует наличие безусловного рефлекса.

Чтобы выработать условный рефлекс, необходимо некоторое время подавать совместно раздражители G и F.

При этом в результате каждого возбуждения пары входов G и F возбуждается нейрон Р, нейрон Q не возбуждается. Импульсы при совпадении G и F накапливаются в счетчике R, выход которого возбуждается только тогда, когда число пришедших импульсов превзойдет некоторую фиксированную величину. С выхода R возбуждение передается на нейрон М (h = l) с петлей обратной связи. Этот нейрон играет роль ячейки памяти. Теперь, если появляется один раздражитель G, возникает реакция А, так как нейрон N (порог h = 2) имеет один возбужденный вход (концевая пластина нейрона М). Условный рефлекс выработан. Если теперь на схему подается только сигнал G, то будет возбуждаться нейрон Q. Возбуждение нейрона Q передается на счетчик S и, если событие GΛ¯F повторяется несколько раз подряд, возбудится аксон счетчика, имеющий концевую тормозящую пластину на нейроне М, нейрон М тормозится – рефлекс угасает.

Если в процессе обучения наряду с событием GΛF происходит событие GΛ¯F, то возбуждается нейрон Q и происходит сброс счетчика R. Обучение нужно начинать сначала. Аналогичная ситуация наблюдается при гашении рефлекса.

Рассмотрим, какие законы накопления и нейтрализации возбуждения реализуют операторы R и S. Из рассмотрения схемы нервной сети видно, что оператор R реализует следующую функцию:

r₁ = r + 1,

где r – содержимое накопителя. Порог накопителя h – фиксированная величина.

Оператор S более сложен; его можно представить в таком виде:

...р (r < h) ¹↑ ²↓ ¯R ω ³↑ ¹↓ S₁ p(s > h₁) ²↑ ³↓…

Здесь оператор ¯R означает нейтрализацию всего содержимого в накопителе R, т. е. ¯R(r)=0; оператор S₁ реализуется функцией:

s₁ = s + 1,

где: s – содержимое счетчика «забывания»; h₁ – порог счетчика забывания.

Таким образом, рефлекс образуется только в том случае, если происходит h раз подряд событие GΛF и при этом ни разу не происходит событие GΛ¯F.

Это, вероятно, не совсем точно согласуется с данными физиологических экспериментов. А.А. Ляпунов (1958) присваивал другое содержание операторам R и S. Величина r после каждого эксперимента пересчитывается по закону:

r₁ = r + η + δ,

где: η – некоторая случайная величина с математическим ожиданием, равным 0; δ – приращение, которое может быть положительным или отрицательным в зависимости от того, применяется оператор R или S.

Каким образом в действительности реализуется закон накопления возбуждения, еще неясно. Для выяснения этого вопроса необходимо поставить серию физиологических экспериментов с целью выявления закона распределения вероятностей числа необходимых повторений события GΛF, чтобы рефлекс выработался. Из этого простого примера понятно, что точное алгоритмическое описание процесса может вызвать необходимость ставить новые эксперименты и точно указать, какие именно эксперименты следует проводить для точного представления всего процесса в целом. Возможность полного алгоритмического описания процесса указывает на его изученность (конечно, здесь имеются в виду лишь информационные связи, а не энергетические).

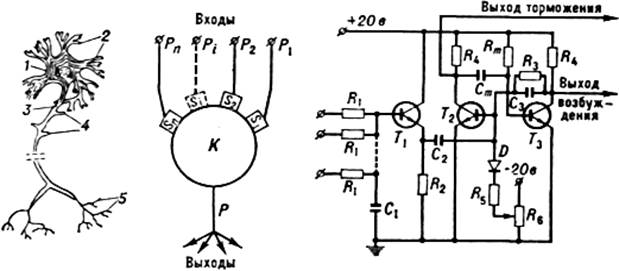
Описание модели условного рефлекса было бы не полным, если не привести пример имитационного моделирования самого нейрона. На рис. 1.2 приведена такая модель и ее электрическая схема.

Электронные нейроны, изображенные на рис. 1.2, объединенные в схему рис. 1.1 и составят имитационную модель классического обусловливания.

Важным принципом оперантного обусловливания является то, что реакции, за которыми следует вознаграждение или позитивное подкрепление, имеют тенденцию к усилению, тогда как реакции, которые не вознаграждаются, идут на убыль.

Рис. 1.2. Схематическое изображение нейрона (слева), его модели (в середине) и электрической схемы искусственного нейрона (справа):
1 – тело клетки; 2 – дендриты; 3 – аксон; 4 – коллатерали; 5 – концевое разветвление аксона.	Рn, Рi, Р2, P1 – входы нейрона; Sn, Si, S2, S1 – синапсические контакты; Р – выходной сигнал; К – пороговое значение сигнала;	R1 – R5, Rm – сопротивления; C1 – C3, Cm – конденсаторы; T1 – T3 – транзисторы; D – диод; R6 – резистор, задающий порог пропускания

Одним из основных сторонником планов с малым n следует назвать Скиннера, который наблюдал эволюцию поведения у одного испытуемого. Скиннер продемонстрировал этот принцип опытами на крысах, определяя, усиливается ли реакция, состоящая в нажатии на рычаг, после вознаграждения. Изобретенное Скиннером приспособление было названо «ящиком Скиннера». Первоначальное поведение крысы, помещенной в «ящик Скиннера», является по сути естественным поисковым поведением: она обнюхивает углы, перемещается от одной стенки к другой, изучает их, умывает мордочку. Лишь небольшая часть этих реакций имеет что-то общее с реакцией нажатия на рычаг, но опытный исследователь может идентифицировать реакции, предшествующие нажатию на рычаг, и подкрепить их. Процесс избирательно подкрепляемого последовательного приближения к основной реакции (нажатие на рычаг) называется целенаправленным формированием. Животное постепенно подходит все ближе к рычагу, затем ставит свою лапку рядом с рычагом, касается его и, наконец, надавливает на него.

Собрано много данных, относящихся к конкретным условиям, которые облегчают оперантное обусловливание. Например, если вознаграждение следует сразу же за необходимой реакцией, тогда обусловливание происходит быстрее, чем в том случае, когда вознаграждение происходит с задержкой.

Другие исследователи изучили то влияние, которое оказывает на поведение вторичное подкрепление (стимулы, которые связаны с первичным вознаграждением). Основной вывод на основании этих исследований таков: вторичное подкрепление обладает сильным свойством вознаграждения. Вспомните о тех свойствах вознаграждения, которыми обладает во многих обществах вторичное подкрепление в виде денег. В этом исследовании Прайор, Хаага и О'Рейлли (1969) использовали в качестве обусловленного подкрепления свист, как хорошо различимый сигнал.

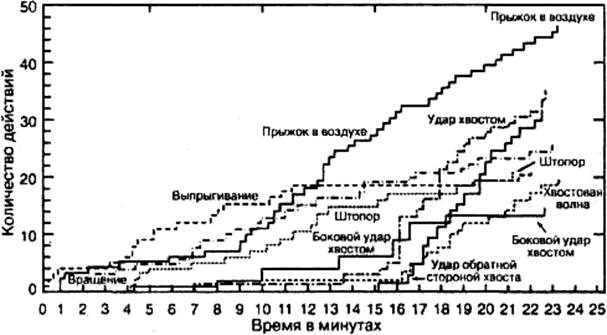
Рис. 1.3. Кумулятивная диаграмма занятия 16, во время которого подопытное животное (дельфин) продемонстрировало 8 различных типов реакций, причем 4 из них наблюдались впервые (прыжок в воздух, вращение, боковой удар хвостом и удар обратной стороной хвоста) [9]

Результаты экспериментов с операционным обусловливанием представляются графически в виде диаграммы кумулятивной (накопленной) частоты (рис. 1.3). На таком графике реакции подопытного животного аккумулируются и изображаются на оси ординат, а на оси абсцисс отмечается время. Поскольку реакции складываются, кривая реакции всегда идет вверх; случаи отсутствия реакции показываются линией, параллельной оси абсцисс.

Контрольные вопросы

1. Что такое экспериментальный план с малым объемом выборки n?

2. В каких отраслях наук о человеке применяются экспериментальные планы с малыми n?

3. Что такое классическое обусловливание?

4. Что такое оперантное обусловливание?

ЭКСПЕРИМЕНТАЛЬНЫЕ ПЛАНЫ

С БОЛЬШИМИ ОБЪЕМАМИ ВЫБОРОК

В общем случае любой эксперимент проводится или в целях определения сходства/различия (близости/удаленности) между объектами-признаками; либо в целях определения связи признаков «Х1» и «Х2», измеренных в одинаковых условиях.

Пример для первого случая.Необходимо проверить эффективность методики развития координационных способностей у баскетболистов. Объектами будут служить спортсмены, а признаком – показатель координационных способностей.

Формируем две группы – контрольную и экспериментальную – и проводим первичное испытание координационных способностей. Например, регистрируем количество попаданий мяча в корзину из 20 попыток – параметр «Х».

Теперь мы должны сравнить, насколько результаты тестирования признака «Х» в одной группе (контрольной) отличаются от результатов другой (экспериментальной). После первичного испытания (Х1) статистически достоверного различия между результатами тестирования обеих групп быть не должно.

Испытуемых обеих групп начали тренировать, развивая исследуемое качество, используя две разные методики (к примеру, методом подражания и методом исключения избыточных степеней свободы движения).

По прохождении курса обучения проводим повторное тестирование (X2) обеих групп. Теперь результаты тестирования признака «Х» должны статистически достоверно различаться.

Затем по более высокой динамике исследуемого признака «Х» определяется эффективность методики.

Пример для второго случая.Параллельно с регистрацией количества попаданий мячом в корзину из 20 попыток (признак «Х»), измеряется время выполнения теста в секундах (признак «Y»).

Замечено, что спортсмены более высокого уровня затрачивают меньше времени на выполнение теста с лучшей результативностью. Между признаками «X» и «Y» существует статистически достоверная связь, описываемая математической формулой.

Прекрасный пример экспериментального плана с большим объемом выборки в спорте приведен в прил. 2.

Измерение признаков объектов позволяет создавать базы данных; выявление закономерностей взаимосвязей признаков или объектов – базы знаний.

После того как признак объекта зарегистрирован и измерен, данные могут быть представлены в различной качественно-количественной форме, в различных шкалах.