показателей древостоев
Известно более 77 функций, применяющихся для описания лесообразовательных процессов. Нам важны те из них, которые путем преобразований можно свести к линейной функции и использовать непосредственно при расчетах. По литературным источникам такие функции были подобраны. Они рассмотрены ниже. В курсовой работе студенты, описывая расчетные данные, анализируют все указанные функции, затем выбирают из них ту, которая наилучшим образом описывает динамику таксационного признака.
1) Линейная регрессияимеет следующий вид:
уt² = а + bх. (4.1)
Параметры уравнения находят по методунаименьших квадратов.
Для того чтобы найти параметры модели, необходимо приравнять нулю первые производные по каждому из коэффициентов. Решая систему уравнений с k неизвестными, находим значения коэффициента ai.
Параметры b и а вычисляются по формулам
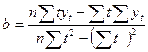 ; (4.2)
; (4.2)
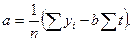 (4.3)
(4.3)
Параметр b называют коэффициентом регрессии. Он характеризует угол наклона линии регрессии над осью абсцисс. Параметр а является свободным коэффициентом линейного уравнения и указывает на начальную величину анализируемого признака, отсекаемую линией регрессии на оси ординат при значении аргумента, равном нулю.
В реальном мире большинство функций роста являются нелинейными по параметрам. При таких функциях для минимизации функционала необходимы методы нелинейного программирования. Однако понимание очень простых линейных связей способствует пониманию также и нелинейных отношений. Есть кривые, которые путем простейших преобразований левой или правой частей уравнения можно свести к линейному тренду. Такие функции являются внутренне линейными. К этому классу относится часть функций дробных и степенных преобразований. Расчеты с ними можно проводить при наличии калькулятора. В тал. 4.1 показан пример расчета хода роста в высоту лиственничников.
Таблица 4.1. Динамикавысот лиственничников V класса бонитета
| А | t | t2 | yt / lnyt = Yt | yt 2 / Yt2 | t yt / t Yt |
| 5,60 1,722 | 31,36 / 2,96 | 5,60 / 1,72 | |||
| 6,08 1,805 | 36,97 / 3,26 | 12,16 / 3,61 | |||
| 6,85 1,924 | 46,92 / 3,70 | 20,55 / 5,77 | |||
| 8,07 2,088 | 65,12 / 4,36 | 32,28 / 8,35 | |||
| 8,39 2,127 | 70,39 / 4,52 | 41,95 / 10,64 | |||
| 9,14 2,212 | 83,54 / 4,90 | 54,84 / 13,27 | |||
| 11,00 2,398 | 121,00 / 5,75 | 77,00 / 16,79 | |||
| 11,96 2,481 | 143,04 / 6,16 | 95,68 / 19,85 | |||
| 14,90 2,701 | 224,70 / 7,30 | 134,91 / 24,31 | |||
| 15,74 2,756 | 247,75 / 7,60 | 157,40 / 27,56 | |||
| 15,13 2,717 | 228,92 / 7,38 | 166,43 / 29,89 | |||
| S | 112,95 24,931 | 1299,71 / 57,89 | 798,80 / 161,76 |
Примечание: А – возраст, лет; t – нормированный возраст; yt" – высота древостоя лиственницы, м.
Подставляя в уравнения (4.2) и (4.3) итоговые данные табл. 4.1, находим параметры b и a:
b = 11 × 798,80 - 66 × 112,95 / 11 × 506 - (66)2.
b = 8786,8 - 7454,7 / 1210 = 1332,1 / 1210 = 1,1009.
a = 112,95 / 11 - 1,1009 × 66 / 11 = 10,268 - 6,605 = 3,663.
Подобранное уравнение можно использовать для прогноза высоты древостоя лиственницы. Расчеты показывают, что анализируемое насаждение, при отсутствии пожаров, к 240 летнему возрасту будет иметь высоту 16,9 м:
y12 ² = 3,663 + 1,1009 × 12 = 16,87 м.
Конечно, эти данные отличаются от фактической высоты, однако их можно использовать как ориентир при расчетах продуктивности древостоев.
2) Простая экспоненциальная кривая.Для описания биологических и лесохозяйственных процессов широко применяют простую экспоненциальную кривую. Она описывается уравнением вида
уt² = аeвt, (4.4)
или yt² = ea¢+bt, где а¢ = ln a, или yt ² = a(b¢)t, где b¢ = eb.
Чтобы перейти к линейному виду регрессии, от обеих частей уравнения (4.4) надо взять натуральный логарифм
ln yt = ln a + b t lnе, при этом ln e = 1.
Переобозначим зависимую переменную ln yt = Yt , и уравнение (4.4) можно записать в новом виде:
Yt = a¢ + b t.
В этом уравнении a¢ (= ln a) и b могут быть найдены с помощью стандартной процедуры линейного регрессионного анализа, которая рассмотрена в табл. 4.2.
Таблица 4.2. Подгонка экспоненты
| Переменная | Зависимая | Независимая |
| Вид преобразования | Yt = ln yt | T |
| n = 11 | åYt = 24,93; åYt2 = 57,89 | åt = 66; åt2 = 506; åtYt = 161,76 |
Примечание: по данным, приведенным в табл. 4.1.
b = 11 × 161,76 – 66 × 24,931 / 11 × 506 - 662 = 1779,36 - 1645,45 / 1210 =
133,91 / 1210 = 0,1105;
а¢ = 24,931 - 0,1105 × 66 / 11 = 24,931 – 7,293 / 11 = 1,6034
а = antiln 1,603 = 4,970;
yt ² = 4,970e 0,1105 t.
С помощью уравнения (4.4) можно прогнозировать рост древостоев в высоту. Например, для t, равного 12, значение зависимой переменной будет равно y12² = 4,97e1,326 = 18,7 м.
Важное свойство простой экспоненты − темп роста. При b > 0 он постоянен для любого отрезка времени на этой кривой. В экономических расчетах ее используют для оценки темпов инфляции, в биологических исследованиях − темпов роста.
3) Степенная кривая.Уравнение степенной кривой передается следующими параметрами:
уt² = аtb. (4.5)
Если взять натуральный логарифм от обеих частей уравнения, оно примет следующий вид: ln yt" = ln a + b ln t. Обозначим зависимую переменную ln yt как Yt, а независимую переменную t как T = ln t. Тогда степенное уравнение можно записать следующим образом:
Yt = a¢ + bT.
Для вычисления значений а (= antiln a¢) и b применяется стандартная процедура линейной регрессии, итоговые данные которой приведены в табл. 4.3.
Таблица 4.3. Подгонка степенной кривой
| Переменная | Зависимая | Независимая |
| Вид преобразования | Yt = ln yt | T = ln t |
| Sn = 11 | SYt = 24,93, SYt2 = 57,89 | ST = 17,50 ST2 = 33,40 STYt = 42,28 |
Примечание: по данным, приведенным в табл. 5.1.
b = 11 × 42,28 - 17,50 × 24,93 / 11 × 33,40 - (17,5)2 = 468,08 - 436,28 / 60,15 =
= 31,8 / 60,15 = 0,529.
a¢ = 24,93 - 0,529 × 17,5 / 11 = 1,425.
yt ²= 4,549 t 0,529.
Степенная кривая при b = -1 имеет вид yt² = a/t.Это уравнение задает гиперболу, асимптотами которой являются оси координат, а произведение (yt²× t = a) постоянно. В экономике этому условию удовлетворяет кривая спроса с единичной эластичностью: процент увеличения единицы времени t приводит к такому же проценту уменьшения зависимой переменной yt. Прогноз на 2001 г. составил: y12²= 4,549 × 12 0,529 = 15,79 м .
4) Гиперболическая функция I типа.Гипербола I типа задается уравнением
yt ² = a+b/t. (4.6)
К линейному виду ее приводят простым преобразованием независимой переменной t, заменяя ее на выражение 1/t = T. Тогда уравнение (4.6) перепишется в следующем виде
yt² = a + bT .
Значения параметров a и b находятся стандартными методами регрессионного анализа. Результаты расчетов сведены в табл. 4.4.
Таблица 4.4. Подгонка гиперболической кривой I типа
| Переменная | Зависимая | Независимая |
| Вид преобразования | уt | T = 1/t |
| n = 11 | Syt = 112,95; Syt2 = 1299,71 | ST = 3,02; ST2 = 1,56; ST yt" = 23,82 |
Примечание: по данным, приведенным в табл. 4.1.
Параметр b = (nS Tyt - STS yt ) / [nST2 - (ST)2];
b = 11 × 23,82 - 3,02 × 112,95 / 11 × 1,56 - (3,02)2;
b = 262,02 - 341,11 / 8,04 = 78,91 / 8,04 = - 9,82.
Параметр a= (Syt -- b ST) / n = (112,95 + 9,82 × 3,02) / 11 = 12,97.
Уравнение гиперболы имеет следующий вид: yt² = 12,97 - 9,82 / t.
При значениях b > 0 значение yt² уменьшается, с увеличением t − асимптотически приближается к a. При значении b < 0 зависимая переменная положительна при условии, если t > b/a. Увеличение t в этом случае приводит к увеличению yt” с асимптотической границей, равной а. Прогноз роста в высоту с помощью уравнения гиперболы I типа составил
y12² = 12,97 - 9,82 / 12 = 12,16 м.
По сравнению с другими уравнениями гипербола I типа дала самый минимальную высоту. Но это еще не говорит о том, что ее нельзя использовать для прогноза. Прогностические возможности функций определяются доверительными интервалами.
5) Гиперболическая кривая II типа.Гиперболическая кривая II типа имеет выражение
yt² = 1/(a + bt). (4.7)
К линейному виду, в отличие от гиперболы I типа, уравнение (4.7) приводят с помощью обратного преобразования зависимой переменной yt.. Таким образом, если Yt = 1/ yt , то уравнение (4.7) можно переписать в таком виде:
Y t = a + bt.
Дальнейшие расчеты с новым уравнением проводятся согласно стандартной процедуре линейной регрессии. Итоговые данные приведены в табл. 4.5.
Таблица 4.5. Подгонка гиперболической кривой II типа
| Переменная | Зависимая | Независимая |
| Вид преобразования | Yt = 1/yt | T = t |
| n = 11 | SYt = 1,212; SYt2 = 0,0015 | St = 66; St2 = 506; S tYt = 5,96 |
Примечание: по данным, приведенным в табл. 4.1.
Параметр b = ( nS tYt - StSYt ) / [ (nSt2 - (St)2 ];
b = ( 11 × 5,96 – 66 × 1,212 ) / ( 5566 – 4356 ) = ( 65,56 - 79,99 ) / 1210 =
- 14,43 / 1210 = - 0, 01193.
a = ( SYt - bSt ) / n = ( 1,212 + 0,01193 × 66 ) / 11 = 1,999 / 11 = 0,1818.
yt² = 1/(0, 1818 - 0,01193 t). Прогноз на 2001 г. составил:
y12² = 1 / ( 0,1818 - 0,01193 × 12 ) = 25,91 м.
Дляэтого типа гиперболыпри b>0 значения зависимой переменной стремятся к нулю. При b<0 yt стремится к бесконечности.
6) Гиперболическая кривая III типа.Гиперболическая кривая задается уравнением вида:
yt² = t/(a + bt ) (4.8)
Ее часто называют простой рациональной зависимостью. К линейному уравнению гипербола III типа сводится путем перехода к обратным величинам преобразования зависимой (Yt = 1/yt" ) и независимой (T = 1/t ) переменных. Новое уравнение записывается в виде
Yt = a¢T + b¢.
Значения a¢ и b¢ находятся стандартным способом с помощью линейной регрессии методом наименьших квадратов. Но следует помнить, что смысл коэффициентов уравнения изменился. Они как бы поменялись местами. Для уравнения (4.8) параметр a = b¢ и b = a¢. Итоговые данные подгонки гиперболы III типа приведены в табл. 4.6.
Таблица 4.6. Подгонка гиперболической кривой III типа
| Переменная | Зависимая | Независимая |
| Вид преобразования | Yt =1/yt | T =1/t |
| n = 11 | SYt = 1,212; SYt2 = 0,0015 | ST = 3,02 ST2 = 1,56 S T yt = 0,426 |
Примечание: по данным, приведенным в табл. 4.1.
b¢ = ( nS T yt - STSYt )/[ ( nST2 - (ST)2] =
= (11 × 0,426 - 3,02 × 1,212 )/(17,16 - 9,12) = 0,128.
a¢ = (SYt - bST)/n = (1,212 - 0,128 × 3,02)/11 = 0,825/11 = 0,075.
Уравнение гиперболы III типа имеет следующие конкретные параметры: yt²= t/(0,128 + 0, 075t ).
Но для выполнения расчетов надо помнить, что параметр a = b¢ = 0,128 и b = a¢ = 0,075. Прогноз для t = 12 будет равен:
y12² = 12/( 0,128 + 0,075 × 12 ) = 12/1,028 = 11,67 м.
Для этого типа гиперболы при t, равном 0, yt = 0 независимо от значений параметра b. Если b - величина положительная, значение yt возрастает и асимптотически стремится к величине 1/b при неограниченном увеличении t. При отрицательных значениях параметра b эта кривая становится неустойчивой при t = a/b.
7) Логарифмическая кривая.Этот тип кривой задается следующим уравнением:
yt² = a + b ln t. (4.9)
Заменяя в уравнении (4.9) ln t на T, мы приводим его к линейному виду
yt² = a + b T.
Теперь, используя данные табл. 4.1, параметры нового уравнения можно найти по стандартной процедуре линейной регрессии.
b = (nSTyt - S TSyt)/[nST2 - (ST)2 = (11 × 203,43 - 17,5 × 112,95)/[11 × 33,4 –
(17,5)2] = 261,11/60,15 = 4,341.
a = (Syt - b ST)/n = (112,95 - 4,341 × 17,5)/11 = 36,98/11 = 3,362.
Таблица 4.7. Подгонка логарифмической кривой
| Переменная | Зависимая | Независимая |
| Вид преобразования | yt | T = ln t |
| n = 11 | Syt = 112,95; Syt2 = 1299,71 | ST = 17,50 ST2 = 33,40 S T yt = 203,43 |
Параметры логарифмического уравнения определены. Оно принимает следующий вид: yt² = 3,362 + 4,341 ln t.
Прогноз составил: y12² = 3,362 + 4,341 ln 12 = 14,15 м.
8) S-образная кривая.S-образная кривая определяется выражением:
yt² = ea+b/t. (4.10)
Если от обеих частей уравнения (4.10) взять натуральный логарифм, оно примет следующий вид:
ln y²t = a + b/t.
После логарифмического преобразования зависимой переменной (Yt = ln yt) и обратного преобразования независимой переменной (T= 1/t) уравнение трансформируется в линейную функцию:
Yt = a + b T.
Коэффициенты a и b вычисляются стандартным способом (табл. 4.8)
Таблица 4.8. Подгонка S-образной кривой
| Переменная | Зависимая | Независимая |
| Вид преобразования | Yt = ln yt | T = 1/t |
| n = 11 | SYt = 24,93 SYt2 = 0,0015 | ST = 3,02 ST2 = 1,56 S T Yt = 6,03 |
b = (nS T Yt - STSYt )/[ nST2 - (ST)2] = (11 ×6,03 - 3,02 × 24,93)/[11 × 1,56 –
(3,02)2] = 8,86/8,04 = - 1,10;
a = (SYt - b ST )/ n = (24,93 + 1,10 × 3,02) / 11 = 28,25/11 = 2,568.
Уравнение (4.10) имеет следующий вид:
yt² = e2,568 - 1,10/t.
По этому уравнению можно находить выровненные значения зависимой переменной и прогноз на перспективу: y12² = e2,568 - 1,10/12 = 11,9 м.
S-образную форму эта кривая имеет при двух условиях: отрицательном значении параметра b и его абсолютном превышении над параметром а. В нашем примере соблюдено только одно условие, поэтому кривая не имеет точки перегиба. Надо отметить, что S-образные кривые широко используются в научных исследованиях при описании динамических процессов. Для них характерен замедленный рост в начальный период, затем наступает стадия активного роста, которая в завершении асимптотически приближается к некоторому уровню, близкому значению eа. Для S-образной кривой точкой перегиба (время, в котором рост коэффициента наклона касательной сменяется падением) будет точка
t = - b/2. Более формально точка перегиба характеризуется скоростью роста анализируемого признака, и там, где он достигает своей максимальной величины, будет точка перегиба. Математически она находится решением уравнения f¢¢ (t) = 0, где f¢¢ − вторая производная по t кривой f. Решая дифференциальное уравнение для S-образной кривой, получаем, что t = –b/2. Отсюда, меняя параметр b, можно подобрать для S-образной кривой свои точки перегиба. Например, при b = 10 точка перегиба t будет равна 5. А это соответствует 100-летнему возрасту. На практике подобные зависимости не часто описывают S-образной кривой. Для этой цели используют кривую Гомперца и логистическую функцию.
9) Обратнологарифмическая кривая.Это уравнение записывается в следующем виде:
yt² = 1/(a + blnt). (4.11)
Для зависимой переменной yt выполним обратное преобразование (Yt = 1/ yt), а для независимой t – логарифмирование (T = ln t). После этого уравнение (4.11) можно записать как линейное:
Yt = a + bT.
Параметры а и b теперь можно найти с помощью стандартной процедуры линейной регрессии. Итоговые данные расчетов помещены в табл. 4.9.
Таблица 4.9. Подгонка обратнологарифмической кривой
| Переменная | Зависимая | Независимая |
| Вид преобразования | Yt = 1/yt | T = ln t |
| n = 11 | SYt = 1,22 SYt2 = 0,0015 | ST = 17,50 ST2 = 33,23 S T Yt = 1,64 |
Примечание: по данным, приведенным в табл. 4.1.
b = (nSTYt - STSYt)/[nST2 - (ST)2] = (11 × 1,64 - 17,5 × 1,22)/[11 × 33,23 - (17,5)2 = (18,04 - 21,35)/365,5 - 306,25] = - 3,31/59,25 = - 0,05586.
a = (SYt - bST)/ n = (1,22 + 0,05586 × 17,5)/11 = 2,1976/11 = 0,1999.
Уравнение (4.11) запишем в следующем виде: yt² = 1/(0,1999 - 0,05586 ln t).
Прогноз на следующее десятилетие равен: y12² = 1/(0,1999 - 0,05586 ln12) = 1/0,0611 = 16,36 м.
Применение обратнологарифмической кривой в практике прогнозирования обусловлено в первую очередь возможностью перехода к линейному уравнению через логарифмирование и обратное преобразование. Для описания биологических процессов это наименее удачная функция. Иногда ее привлекают для описания коротковосстановительных стадий лесообразовательного процесса.
10) Оценка подобранных уравнений регрессии.Чтобы выбрать из подобранных уравнений регрессии лучшее, осуществляют их оценку. Для этого вычисляют дисперсию зависимой переменной в зависимости от t и сравнивают ее с общей дисперсией, которая не зависит от t. Любая линия регрессии, включая и подобранные, проходит через среднюю точку. Для линейного уравнения средние значения будут следующие: y¢ = 10,26 и t¢ = 6.
Общая дисперсия ряда наблюдений измеряется суммой квадратов разностей (отклонений) между фактическими значениями признака yt и их средним значением у¢. Таким образом, общая дисперсия sобщ может быть вычислена по формуле
s общ = å (yt - y¢)2, (4.12)
где y¢ = 1/n å yt .
При вычислении лучше пользоваться формулой
s общ =å yt2 - (å yt)2/n.
Для данных, помещенных в табл. 4.1, общая дисперсия составила s общ= 1299,71 - 112,952/11 = 139,92.
Подобранные уравнения регрессии связывают определенную часть дисперсии. Естественно, чем теснее связь между зависимой и независимой переменными, тем большая доля дисперсии будет объясняться регрессией. Эту часть дисперсии называют объясняемой (s¢объяс). Она измеряется суммой квадратов отклонений между выравненными экспериментальными данными yt² и их средним значением y¢. Последнее вычисляется по формуле y¢ = 1/ nå yt.
Итак, формула для вычисления объясняемой дисперсии имеет вид
s¢объяс= å (yt² - y¢)2. (4.13)
Для облегчения расчетов ее лучше переписать в другом виде
s¢объяс = b2 [ åt2 - (åt)2 /n],
или
s¢объяс = a åyt + båt yt - 1/n(åt)2.
Для примера с ростом древостоев объясняемая дисперсия линейного уравнения равна
s¢объяс = 1,102 [506 - 662 / 11] = 1,21/110 = 133,32,
или
s¢объяс = 3,7 × 112,9 + 1,10 × 798,8 – 1/ 11 × 112,952 = 134,61.
Дисперсию, которую нельзя объяснить с помощью подобранного уравнения, называют остаточной (s¢ост). Онавычисляется как сумма квадратов разностей между фактическими значениями yt и выравненными по уравнению регрессии yt¢¢:
s¢ост = å (yt - yt²)2. (4.14)
Иногда ее находят как разность между общей и объясняемой дисперсией:
s¢ост = sобщ - s¢объяс = 139,92 - 134,61 = 5,31.
Ее можно найти по следующему уравнению:
s¢ост = åyt2 - aåyt - båt yt. (4.15) (5.15)
Подставим значения сумм из табл. 4.1 в уравнение (4.15)
s¢ост = 1299,71- 3,663 × 112,95 - 1,1009 × 798,8 = 7,22.
Некоторое несовпадение данных остаточной дисперсии, рассчитанной по разным формулам (26 %), объясняется округлением значений а и b.
Все виды дисперсии сведены в табл. 4.10.
Таблица 4.10. Виды дисперсии в регрессионном анализе
| Вид дисперсии | Краткое описание | Формулы расчета |
| Объясняемая | Варьирование значений анализируемого признака, которые объясняются регрессией | b2(åt2 - (åt)2/n или aåyt + båt yt - åyt2/n |
| Остаточная | Разброс значений анализируемого признака, которые не могут быть объяснены регрессией, т. е. варьирование отклонений фактических значений признака от выровненных | åyt2 - aåyt - båt yt |
| Общая | Общее поле варьирования зависимой переменной | åyt2 - (åyt)2/n |
Виды дисперсии косвенно характеризуют тесноту связи между анализируемыми признаками. Количественным выражением этой связи являются коэффициент корреляции t и корреляционное отношение или коэффициент детерминации t2:
при t = 0 связи между y и t нет;
при t ®+1 связь тесная положительная;
при t ® -1 связь тесная отрицательная.
Коэффициент детерминации (квадрат коэффициента корреляции) определяется как доля общей дисперсии к объясняемой:
t2 = s¢объяс/s общ (4.16)
С помощью формул из табл. 4.10 можно получить формулу для расчета коэффициента детерминации (коэффициент корреляции, возведенный в квадрат):
t2= b2[åt2 - (åt)2/n]/åyt2 - (åyt)2/n (4.17)
Для нашего примера коэффициент детерминации равен
t2 = 134,61/139,92 = 0,962.
Извлекая корень квадратный, получаем коэффициент корреляции t = 0,926.
Коэффициент детерминации всегда величина положительная, в отличие от коэффициента корреляции.
Важным аспектом анализируемых функций является возможность их использования для прогноза изучаемого процесса. Прогноз должен быть реальным. Для этого определяют доверительный интервал или конкретные границы, в которых с определенной степенью уверенности можно ожидать появления прогнозируемого признака. Например, значение прогноза, равное 200, с доверительным интервалом, равным ±30, означает, что с 95 %-й степенью уверенности можно ожидать, что будущее значение признака будет находиться в пределах от 170 до 230. Естественно, чем больше доверительный интервал, тем выше степень уверенности при прогнозе. Минимальная величина доверительного интервала равна средней величине наблюдаемого признака y¢ и t¢.
Чтобы определить доверительный интервал, необходимо найти стандартную ошибку уравнения. Ее часто называют среднеквадратическим отклонением. Она определяется как корень квадратный из суммы квадратов отклонений выравненных значений yt² и их фактических значений yt, деленной на n без 2 степеней свободы. Размерность степеней свободы зависит от количества оцениваемых параметров уравнения. Таким образом,
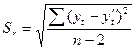 ,(4.18)
,(4.18)
где 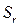 - стандартная ошибка уравнения (среднекавдратическое отклонение).
- стандартная ошибка уравнения (среднекавдратическое отклонение).
Сумму å(yt - y²t)2 можно вычислить как разность между общей суммой квадратов и суммой квадратов выравненных значений.
Стандартная ошибка прогноза находится по формуле:
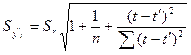 . (4.19)
. (4.19)
Она зависит от числа наблюдений n и расстояния от середины периода до момента прогноза (t - t¢). При большом количестве n отношение 1/n стремится к нулю. И чем дальше прогнозируемый период от середины наблюдения, тем больше ошибка.
Для вычисления стандартной ошибки прогноза отсчет лучше делать от последнего года наблюдения t. Тогда, если период упреждения принять равным r, то в уравнении (4.19) выражение (t - t¢) необходимо заменить на выражение r + (n - 1)/2. Такая процедура переобозначения переменной называется стандартным прогностическим переобозначением. С учетом этих преобразований уравнение (5.19) можно записать как
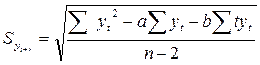
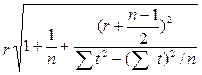 . (4.20)
. (4.20)
Подставляя значения вычисленных сумм, находим ошибку прогноза и его доверительные интервалы. Для получения прогноза с точностью не ниже 99 % его доверительные границы равны ±3Syt+r , 95 % - ±2Syt+r и 68 % - ±Syt+r соответственно.
Для линейного уравнения стандартная ошибка прогноза в 220 лет составила:
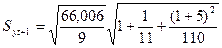 = 0,87 × 1,19 = 1,02 м.
= 0,87 × 1,19 = 1,02 м.
Следовательно, с 95 %-й точностью можем быть уверены, что рост лиственничников в 220 лет не будет больше 18,89 (16,87 ± 2 × 1,02) и меньше 14,85 (16,87 ± 2 × 1,02) м.
Выбор лучшей кривой при подгонке теоретических данных к экспериментальным, как правило, осуществляют по величине коэффициента корреляции. Для наших кривых вместе с параметрами подобранных уравнений регрессии он помещен в табл. 4.11.
Таблица 4.11. Параметры уравнений регрессии и коэффициенты корреляции
| Вид регрессии | Параметр а | Параметр b | Коэффициент корреляции |
| Линейная | 3,663 | 1,1009 | 0,926 (4) |
| Экспонента простая | 4,968 | 1,326 | 0,963 (1) |
| Cтепенная | 4,549 | 0,529 | 0,892 (5) |
| Гиперболическая I типа | 12,973 | - 9,820 | 0,597 (9) |
| Гиперболическая IIтипа | 0,1818 | - 0,01193 | 0,956 (2) |
| Гиперболическая III типа | 0,128 | 0, 075 | 0,784 (7) |
| Логарифмическая | 3,362 | 4,341 | 0,810 (6) |
| S-образная | 2,568 | -1,106 | 0,704 (8) |
| Обратнологарифмическая | 0,1999 | -0,05586 | 0,930 (3) |
По коэффициентам корреляции лучше всех исходные данные описывает простая экспонента, затем гипербола II типа и обратнологарифмическая функции. При подгонке (аппроксимации) аналогичных исходных данных им следует отдавать предпочтение перед другими кривыми. В лесоводственных исследованиях возраст обычно не нормируется. При отсутствии вычислительной техники для облегчения и ускорения расчетов к этому преобразованию можно прибегать. Суть регрессии от этого не меняется. Не снижается и точность описания исходных данных.
11) Модифицированная экспонента.Характеризуя рассмотренные выше функции, следует отметить, что все они описывают ситуации, когда коэффициент наклона касательной имеет либо отрицательный, либо положительный знак. Однако чаще всего в природе, особенно лесных биогеоценозах, встречаются случаи, когда изучаемый признак изменяется неравномерно. Другими словами, кривая, описывающая этот процесс, имеет точку перегиба или на кривой есть точка, где рост наклона касательной сменяется ее падением или наоборот: падение заменяется ростом. Такой рост характерен для экономических и биологических процессов. При их описании чаще всего используют логистическую и кривую Гомперца. Обе эти кривые могут быть получены из модифицированной экспоненты
Модифицированная экспонента занимает особое место при описании различных биологических и экономических процессов. Сама по себе кривая не имеет точки перегиба. Ее уравнение выглядит следующим образом:
yt² = a + b ct. (4.21)
Но на ее основе путем определенных преобразований зависимой переменной можно будет получить другие S-образные кривые: логистическую и кривую Гомперца, которые уже имеют точки перегиба и широко используются при изучении динамических процессов в биологии, экологии, экономике. Они будут рассмотрены ниже. Кривые, построенные на базе модифицированной экспоненты, задаются тремя параметрами (ранее мы рассматривали два). В этой связи они более точно описывают исследуемый процесс, но требуют больших вычислительных работ.
Модифицированная экспонента задается тремя параметрами: а, b и с. При их нахождении процедура метода наименьших квадратов неприложима. Для их определения используют метод, описанный Бриантом. Следуя этому методу, первоначально находят параметр c, затем b и a:
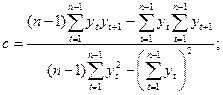 (4.22)
(4.22)
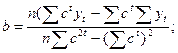 (4.23)
(4.23)
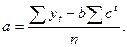 (4.24)
(4.24)
Для сравнения точности подгонки исходные данные для вычисления параметров модифицированной экспоненты взяты из табл. 4.1. Данные расчетов сведены в табл. 4.12.
Обозначения зависимой и независимой переменных остались прежними. Напомним, что первое наблюдение соответствует моменту времени t = 1, а 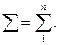 Эти условия сохранились и для других функций – логистической и кривой Гомперца.
Эти условия сохранились и для других функций – логистической и кривой Гомперца.
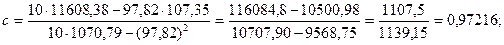
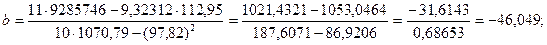
a = (112,95 + 46,049 × 9,32312) / 11 = 542,27 / 11 = 49,30.
Уравнение модифицированной экспоненты можно записать в виде
yt² = 49,3 - 46,049(0,97216) t.
Выполненный на его базе прогноз на 220 лет составил 16,3 м.
Модифицированная экспонента не имеет точки перегиба. Но это не означает, что ее нельзя использовать для подгонки к исходным данным и прогнозирования. В природе встречаются такие явления, когда рост в начальный период имеет высокий темп, потом он стабилизируется и длительное время находится на одном уровне. Как показывает практика, этот процесс лучше всех описывает модифицированная экспонента.
Таблица 4.12. Подгонка модифицированной экспоненты
| t | yt | yt+1 | yt yt+1 | Yt2 | ct | ct yt | c2t | yt ² |
| 5,60 | 6,08 | 34,048 | 31,36 | 0,97216 | 5,44409 | 0,94500 | 4,53 | |
| 6,08 | 6,85 | 41,648 | 36,97 | 0,94509 | 5,74682 | 0,89320 | 5,80 | |
| 6,85 | 8,07 | 55,280 | 46,92 | 0,91889 | 6,29440 | 0,84416 | 6,99 | |
| 8,07 | 8,39 | 67,707 | 65,12 | 7,20901 | 0,79781 | 8,17 | ||
| 8,39 | 9,14 | 76,686 | 70,39 | 0,86844 | 7,28662 | 0,75401 | 9,31 | |
| 9,14 | 11,00 | 10,540 | 83,54 | 0,84416 | 7,71653 | 0,71261 | 10,40 | |
| 11,00 | 11,96 | 131,560 | 121,00 | 0,82066 | 9,02825 | 0,67348 | 11,51 | |
| 11,96 | 14,99 | 179,280 | 143,04 | 0,79781 | 9,54288 | 0,63651 | 12,56 | |
| 14,99 | 15,74 | 235,943 | 224,70 | 0,77560 | 11,62759 | 0,60156 | 13,59 | |
| 15,74 | 15,13 | 238,146 | 247,75 | 0,75401 | 11,86938 | 0,56853 | 14,57 | |
15,13 
| - | - | - | 0,73302 | 11,09180 | 0,53732 | 15,54 | |
| n-1 å t=1 | 97,82 | 107,35 | 1160,838 | 1070,79 | - | - | - | - |
| å | 112,95 | - | - | - | 9,32312 | 92,85746 | 7,96428 | - |
Примечание: по данным, приведенным в табл. 5.1.
12) Кривая Гомперца.Преобразуя модифицированную экспоненту, получают кривую Гомперца и логистическую кривую. Уравнение Гомперца имеет следующий вид
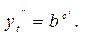 (4.25)
(4.25)
Возьмем от обеих частей уравнения натуральные логарифмы
ln yt² = ln a + ct ln b
и вынесем их за его пределы, подставляя вместо них другие обозначения:
Yt = ln yt²; a¢ = ln a; b¢ = ln b . В итоге получим уравнение Yt = a¢ + b¢ ct.
Оно имеет вид модифицированной экспоненты, поэтому для определения его параметров можно использовать формулы (5.22) – (5.24). Подстановку параметров в уравнение (5.25) осуществляют после нахождения антилогарифмов а (= antiln a’) и b (= antiln b’), и только после этого его можно привлекать для вычисления зависимой переменной и прогноза (табл. 4.12.).
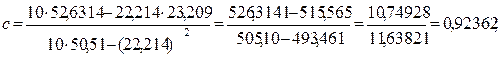
b¢ = 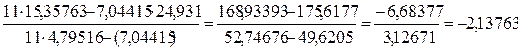 ;
;
a¢ = 24,931 + 2,1376× 7,04415 / 11 = 3,63532.
Уравнение кривой Гомперца будет иметь следующие параметры
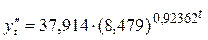 .
.
Прогноз на 220 г. с помощью уравнения Гомперца составил 16,17 м.
Таблица 4.12. Подгонка кривой Гомперца к модифицированной экспоненте
| t | yt | yt+1 | yt yt+1 | Yt2 | ct | ct yt | c2t | yt ² |
| 1,722 | 1,805 | 3,1082 | 2,966 | 0,92362 | 1,59047 | 0,85307 | 4,50 | |
| 1,805 | 1,924 | 3,4728 | 3,26 | 0,85307 | 1,53979 | 0,72774 | 5,77 | |
| 1,924 | 2,088 | 4,0173 | 3,70 | 0,78792 | 1,51596 | 0,62081 | 6,99 | |
| 2,088 | 2,127 | 4,4412 | 4,36 | 0,72774 | 1,51952 | 0,52960 | 8.26 | |
| 2,127 | 2,212 | 4,7049 | 4,52 | 0,67215 | 1,42966 | 0,45179 | 9,34 | |
| 2,212 | 2,398 | 5,3043 | 4,90 | 0,62081 | 1,37323 | 0,38541 | 10,42 | |
| 2,398 | 2,481 | 5,9494 | 5,75 | 0,57339 | 1,37499 | 0,32878 | 11,48 | |
| 2,481 | 2,701 | 6,7012 | 6,61 | 0,52960 | 1,31394 | 0,28047 | 12,52 | |
| 2,701 | 2,756 | 7,4440 | 7,30 | 0,48915 | 1,32119 | 0,23926 | 13,61 | |
| 2,756 | 2,717 | 7,4881 | 7,60 | 0,45179 | 1,24513 | 0,20411 | 14,60 | |
| 2,717 | - | - | - | 0,41728 | 1,13375 | 0,17412 | 15,58 | |
| n-1 å t=1 | 22,214 | 23,209 | 52,6314 | 50,51 | - | - | - | - |
| å | 24,9 |
Дата добавления: 2020-10-14; просмотров: 497;











