Модели таблиц хода роста нормальных насаждений
Моделирование продуктивности модальных, нормальных и оптимальных древостоев
Модели таблиц хода роста нормальных насаждений
Таблицы хода роста нормальных насаждений строятся на основе вероятностных типов и классов роста основных таксационных показателей. Исходные уравнения для их расчета приведены в табл. 4.1-4.3. Переход от классов роста к абсолютным значениям признаков в 100 лет осуществляется по табл. 9 прил. Варианты расчета следующие: 1а – 1 и 2 й вариант, 1- 3 вариант и т.д.
Расчет хода роста в высоту. Зависимость типов роста Тh в высоту от классов бонитета Б описывается уравнением параболы 3-го порядка (h = 0,62):
Th = 1,73 + 0,997Б - 0,2227Б2 + 0,02037Б3. (3.1)
Полученные по уравнению средние значения типов роста следующие:
Класс бонитета 1а l ll lll lV V Vа Vб
Тип роста в высоту 2,5 3,0 3,2 3,4 3,6 4,0 4,6 5,3
Зная номер типа роста из табл. 1 прил., выписывают соответствующие индексные значения высоты. Последние затем перемножаются на абсолютные значения высоты в 100 лет определенного класса бонитета, которые заносятся в таблицу хода роста. В качестве примера показан расчет бонитировочной шкалы лиственничников (табл. 3.1).
Таблица 3.1. Индексы высот лиственничных насаждений
(бонитировочная шкала лиственничников)
| Возраст, лет | Класс бонитета | ||||||
| Ia (2.5) | I (3.0) | II (3.2) | III (3.4) | IV (3.6) | V (4.0) | Va (4.6) | |
Примечание: чтобы получить абсолютное значение высоты необходимо индекс умножить на абсолютную высоту в 100 лет и разделить на 1000. Например, высота древостоев в 170 лет в 3-м классе бонитета неизвестна, но мы знаем, что в 100 лет высота равна 21 м, тогда высота в 170 лет будет равна: Н 170 = J 170 ∙ 21 = 1202 ∙ 21/1000 = 25,2 м.
Расчет хода роста по диаметру. Вероятностные значения типов Td и классов роста Кd по диаметру в зависимости от классов бонитета рассчитаны на основании уравнений регрессии, представленных в табл. 3.2. Динамика абсолютных значений диаметров получена путем перемножения индексов роста (прил., табл. 2) на абсолютную величину диаметра в 100-летнем возрасте, которая установлена через класс роста диаметра (прил., табл. 9). Расчетные данные диаметров заносятся в таблицу хода роста.
Таблица 3.2. Зависимость типов и классов роста по диаметру от классов бонитета
| Уравнение регрессии | Класс бонитета | ||||||
| la | l | ll | lll | lV | V | Va | |
| Td = 4,91 + 0,33Б | 5,2 | 5,6 | 5,9 | 6,2 | 6,5 | 6,9 | 7,2 |
| Td = 3,41 + 0,81Th | 5,5 | 5,8 | 6,0 | 6,2 | 6,4 | 6,7 | 7,2 |
| Td = 2,73 + 0,04Б + 0,98Th | 5,2 | 5,7 | 6,0 | 6,2 | 6,4 | 6,9 | 7,5 |
| Td = 4,56 + 0,34Kd | 4,7 | 5,2 | 5,7 | 6,1 | 6,6 | 7,1 | 7,6 |
| Среднее | 5,2 | 5,6 | 5,9 | 6,2 | 6,5 | 6,9 | 7,4 |
| Kd = -1,05 + 1,43Б | 0,4 | 1,8 | 3,2 | 4,6 | 6,1 | 7,5 | 8,9 |
| Kd = -2,30 + 1,26Б + 0,55Th | 0,4 | 1,9 | 3,3 | 4,6 | 6,0 | 7,5 | 9,1 |
| Среднее | 0,4 | 1,9 | 3,3 | 4,6 | 6,0 | 7,5 | 9,0 |
Расчет хода роста по видовому числу. Вероятностные значения типов Tf и классов роста Kf видового числа получены в результате решения подобранных уравнений регрессии, которые приведены в табл. 3.3. Для расчетов индексных значений видового числа по каждому классу бонитета принимаются средние значения типов и классов роста. Переход от индексных значений видового числа к абсолютным осуществляется путем перемножения индексов роста на абсолютную величину видового числа в 100 лет.
Таблица 3.3. Зависимость типов и классов роста видового числа от классов бонитета
| Уравнение регрессии | Класс бонитета | ||||||
| Ia | I | II | III | IV | V | Va | |
| Tf = 1,19 + 0,44Б | 1,6 | 2,1 | 2,5 | 3,0 | 3,4 | 3,8 | 4,3 |
| Tf = 0,52 + 0,72Th | 2,3 | 2,7 | 2,8 | 3,0 | 3,1 | 3,4 | 3,8 |
| Tf = 6,62 – 0,42 Kf | 1,8 | 2,2 | 2,6 | 3,0 | 3,4 | 3,8 | 4,2 |
| Среднее | 1,9 | 2,3 | 2,6 | 3,0 | 3,3 | 3,7 | 4,1 |
| Kf = 12,68 – 0,95Б | 11,7 | 10,8 | 9,8 | 8,9 | 8,0 | 7,0 | 6,1 |
| Kf = 12,99 – 1,23Тh | 10,0 | 10,9 | 9,9 | 8,8 | 7,8 | 6,8 | 5,7 |
| Kf = 15,16 – 0,77Б – 0,91Th | 12,1 | 10,9 | 10,0 | 9,0 | 8,1 | 6,9 | 5,6 |
| Среднее | 11,9 | 10,9 | 9,9 | 8,9 | 8,0 | 6,9 | 5,8 |
Динамику видовых чисел по классам бонитета можно рассчитать путем подстановки средних значений типов и классов роста в уравнение (3.2).
Конкретный вид уравнений следующий:
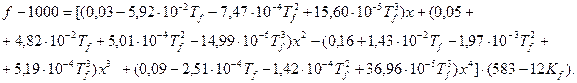 (3.2)
(3.2)
Абсолютные значения видовых чисел заносятся в таблицу хода роста.
Расчет хода роста по сумме площадей сечений. М. М. Орлов считал нормальным такое насаждение, «которое при данных условиях формы, породы, возраста и условий местопроизрастания представляется наиболее возможно совершенным».
Для определения «нормальности» насаждений в таксации использовали разные способы. В одних случаях, на основе массового материала рассчитывают средние значения сумм площадей сечений и их стандартные отклонения. Откладывая от среднего значения определенную величину стандартного отклонения, находят верхний доверительный полуинтервал, который и принимают за высшую полноту. При определении хода роста нормальных по полноте лиственничных насаждений отбирались таблицы максимальной производительности, на основании которых для каждого класса бонитета по формуле:
Кg = 0,05 + 1,07Б (3.3)
были найдены наиболее вероятностные значения классов роста сумм площадей сечений:
Класс бонитета la l ll lll lV V Va
Классы роста сумм
площадей сечений 1,1 2,2 3,3 4,3 5,4 6,5 7,6
Переход от классов роста к абсолютным значениям осуществлен по табл. 9. Значения средних типов роста рассчитаны по уравнению
Tg = 1,05 + 0,41Б. (3.4)
Динамика сумм площадей сечений по классам бонитета получена путем перемножения индексов роста на абсолютное значение признака в 100 лет.
Правильность установления сумм площадей сечений нормальных и модальных насаждений через классы роста проверяют с помощью уравнений
Gнор = 57,95 – 5,35Б; (3.5)
Gмод = 35,80 – 2,80Б. (3.6)
Подставляя класс бонитета в уравнения (3.5) и (3.6), находят вероятностные значения сумм площадей сечений нормальных и модальных насаждений в 100-летнем возрасте, а по ним и динамику этого показателя. Если расчетные значения сумм площадей сечений не превышают 10%, их заносят в таблицу хода роста.
Значения высоты, диаметра, суммы площадей сечений, видового число являются основой для расчета других недостающих показателей. Их находят по следующим формулам.
1) Число стволов древостоя
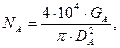 (3.7)
(3.7)
где NA – число стволов древостоя в возрасте A лет, шт.; GA – сумма площадей сечений древостоя в возрасте А лет, м2; DA – средний диаметр древостоя в возрасте А лет, см.
2) Наличный запас
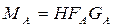 , (3.8)
, (3.8)
где MA – наличный запас древостоя, м3; HFA – видовая высота в возрасте А лет.
3) Среднее изменение запаса древостоя
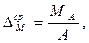 (3.9)
(3.9)
где 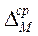 – среднее изменение запаса древостоя, м3.
– среднее изменение запаса древостоя, м3.
4) Текущее изменение запаса
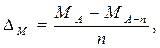 (3.10)
(3.10)
где 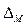 – текущее изменение запаса древостоя, м3; MA - n – запас древостоя n лет назад, м3; n – продолжительность периода.
– текущее изменение запаса древостоя, м3; MA - n – запас древостоя n лет назад, м3; n – продолжительность периода.
Дата добавления: 2020-10-14; просмотров: 630;











