Электрических цепях

С целью упрощения расчета электрической цепи часто оказывается целесообразным осуществить эквивалентное преобразование некоторой части цепи. Часть цепи до преобразования эквивалентна этой же части после преобразования при условии, что режим в остальной непреобразованной части схемы остается неизменным. То есть разность потенциалов между зажимов преобразованной части схемы остается такой же, как и напряжение на зажимах непреобразованной части схемы, а так же входной ток преобразованной части схемы остается неизменным.

Ветвь может содержать любое число последовательно соединенных элементов цепи. При этом последовательным соединением участков электрической цепи называют соединение, при котором через все участки цепи проходит один и тот же ток. При этом напряжение на зажимах этого участка цепи равно сумме напряжений на каждом из ее элементов (рис. 1.7):

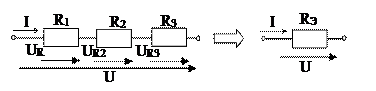
Рис. 1.7

Если мы хотим заменить участок цепи, состоящий из нескольких последовательно соединенных элементов, одним эквивалентным, то напряжение на нем будет равно: .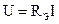

Учитывая условия эквивалентного преобразования, получаем:

.

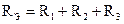То есть при последовательном соединении элементов сопротивление цепи равно сумме сопротивлений составляющих ее элементов.

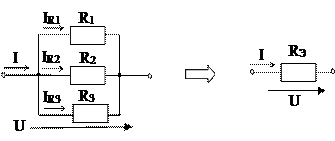Параллельным соединением участков (ветвей) электрической цепи называют соединение, при котором все участки цепи присоединены к одной паре узлов (рис. 1.8), и на всех этих участках имеется одно и то же напряжение.

Рис. 1.8

При этом ток на входе цепи равен сумме токов параллельных ветвей:

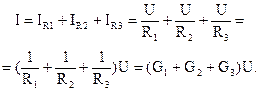
В том случае, если необходимо заменить участок электрической цепи, состоящий их нескольких параллельно соединенных элементов, одним эквивалентным, то ток такого эквивалентного элемента будет определяться: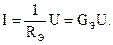

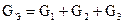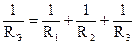Учитывая условия эквивалентного преобразования, можно записать: или , то есть при параллельном соединении приемников для получения эквивалентной проводимости, складывают проводимости параллельных ветвей.

Отсюда можно получить формулу для определения эквивалентного сопротивления:

.

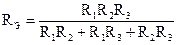Для случая параллельного соединения двух ветвей это выражение буде иметь вид: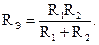

При расчете электрических цепей возникает необходимость эквивалентных преобразований звезды сопротивлений (рис. 1.9, а) в треугольник сопротивлений (рис. 1.9, б). Соединения звездой и треугольником эквивалентны друг другу при условии, что при одинаковых в обоих случаях напряжениях U₁₂, U₂₃, U₃₁ между точками 1, 2 и 3 и токи I₁, I₂, I₃, подходящие к этим точкам от остальной части цепи, одинаковы в обоих случаях.

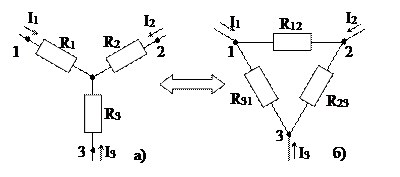Рис. 1.9

Формулы для определения сопротивлений лучей звезды через сопротивления сторон треугольника имеют вид:

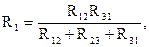
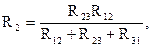
Формулы для расчета сопротивлений сторон треугольника через сопротивления лучей звезды имеют вид:

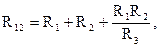
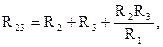
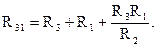
Баланс мощностей

Баланс мощностей является следствием закона сохранения энергии и записывается следующим образом:

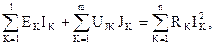
где 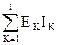– мощность, генерируемая источниками ЭДС;

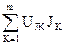– мощность, генерируемая источниками тока;

– мощность, рассеиваемая в резисторах.

Мощность, рассеиваемая в резисторах, всегда положительна. Мощность источников энергии может быть как положительной, так и отрицательной. Отрицательный знак мощности означает, что соответствующий источник работает в режиме потребления электрической энергии.

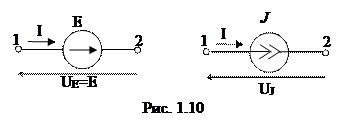Схемы идеальных источников энергии представлены на (рис. 1.10).

Для источника ЭДС мощность P_E = EI положительна, если направления ЭДС источника Е и тока ветви I совпадают, в противном случае мощность отрицательна.

Для источника тока мощность P_J = U_JJ = (φ₂ – φ₁)·J может быть как положительной, так и отрицательной. Если φ₂>φ₁, то мощность положительна, то есть источник работает в режиме генератора. Если же φ₂ < φ₁, то мощность отрицательна и это означает, что источник работает в режиме потребления.

Выполнение баланса мощностей является одним из критериев правильности расчета электрической схемы исследуемой цепи.