Метод узловых потенциалов
Искомыми величинами в методе узловых потенциалов (МУП) являются потенциалы узлов схемы. При этом потенциал одного из узлов принимается равным нулю, а значения потенциалов остальных узлов находятся относительно выбранного нулевого. Определив каждый из искомых узловых потенциалов, нетрудно найти напряжения между любыми парами узлов и токи в ветвях цепи.
При расчете цепей с помощью МУП, используют уравнения, составленные по первому закону Кирхгофа для узлов, потенциалы которых необходимо рассчитать.
Составим уравнения для определения узловых потенциалов схемы рис. 1.13, приняв четвертый узел за опорный, то есть φ4=0. Для чего составим уравнения по первому закону Кирхгофа для остальных узлов:
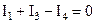 ;
;
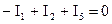 ;
;
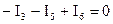 .
.
Выразим токи всех ветвей через потенциалы узлов схемы с помощью закона Ома:
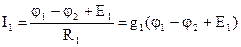 ;
; 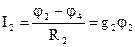 ;
;
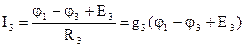 ;
; 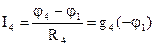
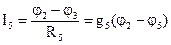 ;
; 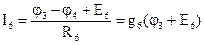 .
.
Подставим значения токов в уравнения, составленные по закону Кирхгофа, и после преобразования получим:
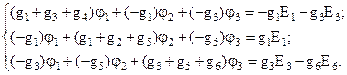
Полученную систему уравнений для определения узловых потенциалов можно записать в общем виде:
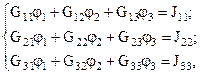
где 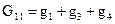 – сумма проводимостей ветвей подходящих к первому узлу;
– сумма проводимостей ветвей подходящих к первому узлу;
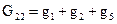 – сумма проводимостей ветвей подходящих ко второму узлу;
– сумма проводимостей ветвей подходящих ко второму узлу;
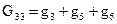 – сумма проводимостей ветвей, подходящих к третьему узлу;
– сумма проводимостей ветвей, подходящих к третьему узлу;
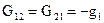 – сумма проводимостей ветвей, включенных непосредственно между первым и вторым узлами;
– сумма проводимостей ветвей, включенных непосредственно между первым и вторым узлами;
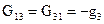 – сумма проводимостей ветвей, включенных непосредственно между первым и третьим узлами;
– сумма проводимостей ветвей, включенных непосредственно между первым и третьим узлами;
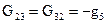 – сумма проводимостей ветвей, включенных непосредственно между вторым и третьим узлами; причем, все диагональные коэффициенты в этой системе уравнений имеют положительный знак, а все недиагональные - отрицательный;
– сумма проводимостей ветвей, включенных непосредственно между вторым и третьим узлами; причем, все диагональные коэффициенты в этой системе уравнений имеют положительный знак, а все недиагональные - отрицательный;
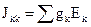 – алгебраическая сумма условных узловых токов, создаваемых ЭДС ветвей, подходящих к k-тому узлу; в том случае если ЭДС направлена к узлу, то создаваемый ею узловой ток входит в сумму с положительным знаком, если же от узла, то с отрицательным:
– алгебраическая сумма условных узловых токов, создаваемых ЭДС ветвей, подходящих к k-тому узлу; в том случае если ЭДС направлена к узлу, то создаваемый ею узловой ток входит в сумму с положительным знаком, если же от узла, то с отрицательным:
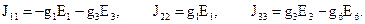
Определив по полученной системе уравнений потенциалы узлов схемы, по закону Ома определяют токи ветвей.
Метод двух узлов
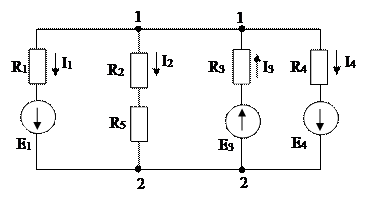
В том случае, если схема (рис. 1.14) имеет только два узла, удобно применять метод двух узлов, который является частным случаем метода узловых потенциалов.
Примем потенциал второго узла равным нулю 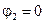 . И определим потенциал первого узла. Согласно МУП необходимо составить одно уравнение:
. И определим потенциал первого узла. Согласно МУП необходимо составить одно уравнение:
 |
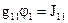 или
или 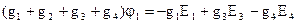 .
.
Рис. 1.14
Откуда потенциал первого узла и напряжение на зажимах параллельных ветвей можно определить:
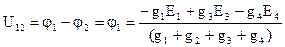 ,
,
или в общем виде:
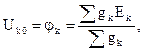
где 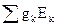 – алгебраическая сумма условных узловых токов, создаваемых ЭДС, подходящих к узлу k;
– алгебраическая сумма условных узловых токов, создаваемых ЭДС, подходящих к узлу k;
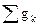 – сумма проводимостей ветвей, подходящих к этому узлу.
– сумма проводимостей ветвей, подходящих к этому узлу.
Метод наложения
Метод наложения, вытекающий из принципа наложения (суперпозиции), справедлив для линейной цепи любой сложности, содержащей несколько источников электрической энергии.
Принцип наложения формулируется следующим образом: ток в k-той ветви сложной линейной электрической цепи, содержащей несколько источников электрической энергии, равен алгебраической сумме частичных токов, вызываемых каждым источником энергии в отдельности.
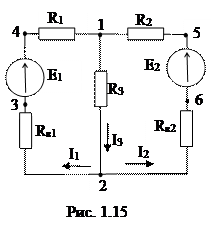 |
Рассчитаем токи в электрической цепи, схема которой приведена на рис. 1.15 методом наложения. Расчет выполняется в следующей последовательности.
Определим частичные токи от действия первого источника ЭДС Е1.
Для этого составим схему (рис. 1.16, а), содержащую только источник ЭДС Е1, а источник ЭДС Е2 из схемы исключим. При этом зажимы источника ЭДС Е2 закорачиваются, а его внутреннее сопротивление RВ2 остается в схеме.
Необходимо заметить, что в схеме с одним источником электрической энергии мы можем сразу правильно показать положительные направления токов во всех ветвях схемы.
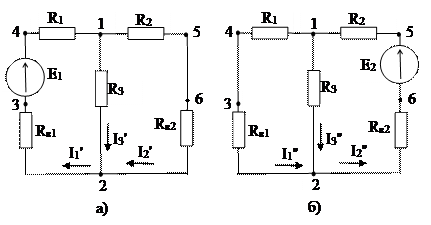 |
Рис. 1.16
Токи в цепи, содержащей один источник ЭДС удобнее всего определять методом эквивалентных преобразований.
Путем постепенного упрощения схемы найдем ее эквивалентное сопротивление относительно зажимов источника ЭДС, что позволит определить ток I1'в неразветвленной части схемы.
Сопротивления второй и третьей ветвей соединены параллельно, поэтому их эквивалентное сопротивление, найденное относительно зажимов 1-2, может быть записано:
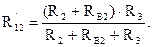
Сопротивление первой ветви и найденное сопротивление R23´ соединены последовательно, поэтому эквивалентное сопротивление относительно зажимов источника ЭДС Е1 находится как: 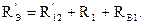
Ток в неразветвленной части схемы определяем по закону Ома: 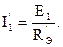
Напряжение между точками 1-2: 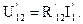
Тогда по закону Ома можно определить ток 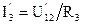 и с помощью первого закона Кирхгофа ток
и с помощью первого закона Кирхгофа ток 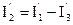 .
.
Определим частичные токи от действия второго источника ЭДС Е2.
Расчет этих токов выполняется аналогично расчету токов от действия первого источника. При этом рассматривается схема (рис. 1.16, б), в которой действует только источник Е2, зажимы источника ЭДС Е1 закорачиваются, но его внутреннее сопротивление RB1 остается в схеме.
Входное сопротивление для определения частичных токов от действия второго источника ЭДС находится относительно зажимов 5-6 этого источника.
Сопротивления первой и третьей ветвей относительно зажимов 1-2 соединены в рассматриваемой схеме параллельно:
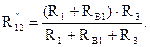
Входное сопротивление относительно зажимов источника ЭДС находим, как последовательное соединение сопротивления второй ветви и сопротивления R12":
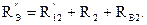
Ток в неразветвленной части цепи: 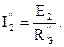
Напряжение между точками 1 и 2: 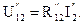
Тогда можно определить токи: 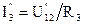 и
и 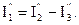
Определим действительные токи в ветвях схемы путем алгебраического суммирования частичных токов. Причем, частичные токи, направление которых совпадает с выбранным ранее положительным направлением действительных токов, берем в этой сумме со знаком «плюс», а те которые не совпадают со знаком «минус»:
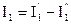 ,
, 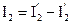 ,
, 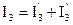 .
.
Дата добавления: 2020-10-14; просмотров: 596;











