Метод контурных токов

Используя метод контурных токов (МКТ) для анализа электрических цепей полагают, что по ветвям каждого независимого контура схемы течет свой контурный ток. Токи всех ветвей схемы можно выразить через эти контурные токи, сократив таким образом количество неизвестных величин. То есть МКТ можно определить как метод расчета, при котором за неизвестные принимают контурные токи. Число контурных токов в МКТ равно числу уравнений, которые необходимо было бы составить для схемы по второму закону Кирхгофа.

Рассмотрим определение токов в ветвях схемы рис. 1.6 методом контурных токов. Пусть по ветвям первого контура протекает контурный ток I₁₁, по ветвям второго – I₂₂, третьего – I₃₃ (рис. 1. 13).

Уравнения, составленные по второму закону Кирхгофа для выбранных контуров, имеют вид:

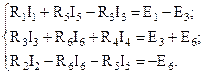
Причем, направления обхода контура выбрано по направлению контурного тока.

Выразим токи ветвей через контурные токи:

, , ,

, , .

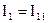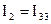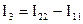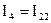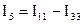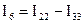Подставим полученные выражения в уравнения, составленные по второму закону Кирхгофа:

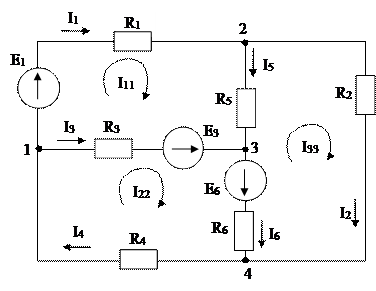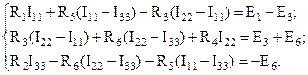
Рис. 1.13

Преобразовав полученную систему уравнений, можно записать:

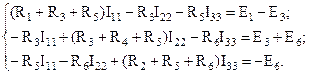
Полученную систему уравнений для определения контурных токов можно записать в общем виде:

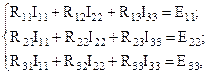
где 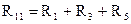– полное или собственное сопротивление первого контура, которое определяется, как сумма сопротивлений в этом контуре;

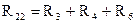– собственное сопротивление второго контура;

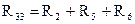– собственное сопротивление третьего контура;

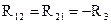– общее сопротивление первого и второго контуров, которое определяется как сумма сопротивлений, одновременно принадлежащих первому и второму контурам, это сопротивление имеет знак «–», если направления контурных токов в общей ветви не совпадают, и знак «+» – если совпадают;

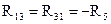– общее сопротивление первого и третьего контуров;

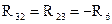– общее сопротивление второго и третьего контуров;

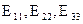– алгебраическая сумма ЭДС в соответствующем контуре, причем, ЭДС, направления которых совпадает с выбранным положительным направлением контурного тока входят в сумму со знаком «+», а которых не совпадают – со знаком «–»:

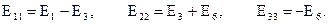
Решив полученную систему уравнений, и определив контурные токи, легко рассчитать токи в ветвях схемы.