Модель Миллена распределения ресурсов (МРР)

Приведенные выше правила ОВО касаются условий, которых необходимо избегать, если мы хотим гарантировать, что действия нарушителя не создадут условий для отказа в обслуживании. Однако среди тех ситуаций, которые могут вызвать угрозу отказа в обслуживании, встречается много таких, которые затрагивают вопросы времени и пространства, не выявляемые простыми правилами типа приведенных выше.

Джонатан Миллен представил модель распределения ресурсов, позволяющую определить правила и стратегии отказа в обслуживании в терминах детального распределения ресурсов, включающего предоставление услуг пользователям вычислительных систем. Модель Миллена отличается от традиционных уровневых правил в моделях БЛМ и Biba, поскольку в ее основе лежит идея о том, что для выполнения нужного задания субъектам необходимы определенные пространственные и временные требования к ресурсам. Отказ в обслуживании происходит в том случае, если распределение пространства и времени для некоторого процесса не отвечает соответствующим требованиям. Миллен показал, что применительно к его модели можно легко объяснить такие понятия, как конечное время ожидания (FWT) и максимальное время ожидания (MWT).

Модель Миллена включает в себя вполне соответствующий стратегии отказа в обслуживании набор правил, характеризующих семейство вычислительных систем, то есть эти правила построены таким образом, чтобы включить в это семейство понятия, которые во многом помогли бы при описании и анализе стратегий отказа в обслуживании. МРР и соответствующие правила представлены ниже.

Пусть Р - множество активных процессов, R - множество пассивных ресурсов, с - некоторая фиксированная граница, используемая для обозначения общего максимального числа единиц всех типов ресурсов, доступных в исследуемой системе. Через вектор распределения A_p обозначим для каждого ресурса число единиц ресурса, выделенных для процесса p в некотором состоянии. Таким образом, вектор распределения можно рассматривать как своего рода отображение выделения ресурсов для процесса. Для формирования информации о том, является ли процесс текущим или застывшим, используется особый тип ресурсов - ресурс ЦПУ. В частности, всякий раз, когда A_p(CPU) = 1, будем говорить, что истинным является running(p), а всякий раз, когда A_p(CPU) = 0, будем говорить, что истинным является asleep(p).

Вектор пространственных требований ^SQ_p означает число единиц каждого ресурса, требуемое процессом p для выполнения необходимого задания в некотором состоянии. Предполагается, что процессы могут определять множество ресурсов, необходимых им для завершения работы, до того, как они ее начнут. Функция T(p) показывает, когда в последний раз изменились часы для процесса с целью отражения реального времени. Вектор временных требований ^TQ_p обозначает объем времени, необходимого каждому ресурсу процесса p для выполнения работы. Как и в случае пространственных требований, предполагается, что процесс может определять временные требования для конкретного задания.

Ниже перечислены восемь правил, составляющих модель Миллена. Каждое правило ограничивает семейство систем, соответствующих этой модели. Прежде чем вводить эти правила, важно заметить, что "помеченные" переменные (например running(p)) показывают значение переменной после одного перехода.

(R1) 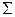A_p ≤ c.

{p 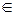P

Правило R1 утверждает, что сумма единиц выделенных ресурсов для всех процессов из P должна быть меньше системной границы c. Стратегии, нарушающие это правило, Миллен называет неправдоподобными, поскольку невозможно выделить ресурсов больше, чем имеется в наличии.

(R2) if running(p) then ^SQ_p= 0.

Правило R2 утверждает, что текущие процессы должны иметь нулевые пространственные требования. Миллен аргументирует это тем, что если процесс не обладает всеми ресурсами, которые необходимы ему в некотором состоянии, то не имеет смысла продолжать этот процесс, пока требования не будут выполнены. "Зависание" происходит, когда процесс имеет ненулевые пространственные требования, которые никогда не будут выполнены (или будут выполнены поздно).

(R3) if running(p) and running(p)' then A_p' = A_p.

Конструкция "running(p) and running(p)' " в правиле R3 означает, что в некотором состоянии процесс p является текущим и остается текущим и в следующем состоянии. Это правило утверждает, что для текущих процессов распределение ресурсов не меняется. Это действительно мощное предположение, поскольку из него следует, что во время выполнения текущие процессы не выгружаются в случае, если произойдет какое-либо перераспределение ресурсов (в отличие от перераспределения ресурсов ЦПУ).

(R4) if A_p(CPU)' =A_p(CPU) then T(p)' = T(p).

Правило R4 утверждает, что часы процесса изменяются только с изменением распределения ЦПУ. Предполагается, что единицы времени - это положительные целые числа, всегда возрастающие с изменением времени (как будет определено ниже).

(R5) if A_p(CPU)' ≠ Ap(CPU) then T(p)' > T(p).

Правило R5 утверждает, что часы изменяются только для того, чтобы отразить увеличение во времени. Заметим, что у каждого процесса имеются свои собственные часы, а синхронизации различных часов друг с другом или с какими-либо часами, показывающими реальное время, не предпринимается.

(R6) if asleep(p) then ^SQ_p' =^SQ_p+A_p - A_p'.

Правило R6 утверждает, что пространственные требования устанавливаются для застывших процессов. Другими словами, если процесс не является текущим, он должен определить те ресурсы, которые ему потребуются для выполнения задания. Как только все эти ресурсы получены, процесс возобновляется и становится текущим.

(R7) if asleep(p) then ^TQ_p' = ^TQ_p.

Правило R7 утверждает, что для застывших процессов временные требования не устанавливаются, то есть тогда как пространственные требования для застывших процессов устанавливаются, временные требования для таких процессов не устанавливаются.

(R8) if running(p) and asleep(p)' then A_p' = A_p - CPU.

Правило R8 утверждает, что переходы, в результате которых процесс останавливается, перераспределяют только ресурсы ЦПУ. Другие изменения в распределении должны происходить после возобновления процесса.

Миллен использует данную модель распределения ресурсов для описания некоторых стратегий. Например, применяя МРР, можно выразить стратегию конечного времени ожидания (FWT). Для указания интервалов, которые могут возникнуть после многократных переходов, мы используем оператор временной логики leads_to (то есть A leads_to B означает, что во всех последующих состояниях из A в конце концов следует В). Для указания интервалов, которые могут возникнуть после многократных переходов, можно выразить максимальное время ожидания (MWT) аналогичным образом.

FWT: " p, s : 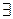s' : s'(running(p)) and s leads_to s'.

В выражении, приведенном выше, s(x) означает, что x истинно для состояния s, а s leads_to s' означает, что " s, s' : s((T(p)=n)) и s'((T(p) =m)) и m>n. FWT утверждает, что пользователи в конце концов получат запрашиваемые ресурсы, то есть они в конечном итоге получат ЦПУ для выполнения работы. Аналогичным образом можно выразить максимальное время ожидания (MWT).

MWT: 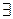b : 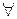p, s : 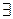s' : s'(running(p)) and s leads_to(b) s'.

В этом выражении s leads_to(b) s' означает, что 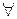s, s' : s((T(p)=n)) и s'((T(p) =m)) и m-n ≤ b. MWT отличается от FWT тем, что здесь накладывается ограничение на время ожидания пользователями возможности продвижения в выполнении задания.

Выводы

Рассмотренные модели безопасности являются очень важной частью защищенной АС, реализуя требуемую политику безопасности. При проектировании защищенных АС должно быть серьезное внимание уделено формированию данных политик.

Вопросы для самоконтроля

1. Перечислите модели разграничения доступа, построенные по принципу предоставления прав. В чем достоинства и недостатки данных моделей?

2. Перечислите вероятностные модели. В чем достоинства и недостатки данных моделей?

3. Чем принципиально отличаются модели дискреционного доступа от моделей мандатного доступа?

4. Как определяется исходная дискреционная модель политики безопасности?

5. Что из себя представляет дискреционная матрица доступов?

6. Как формально определяется модель безопасности Харрисона-Руззо-Ульмана? В чем отличие данной модели от исходной дискреционной?

7. Разрешима ли в общем случае проблема определения безопасности для модели Харрисона-Руззо-Ульмана? Приведите примеры случаев, когда данная проблема разрешима?

8. Как формализуется модель безопасности Белла-ЛаПадулы. Как решается в этой модели проблема программных закладок, записывающих информацию в объекты с более низким уровнем конфиденциальности?

9. В чем заключаются основные отличия политик избирательного разграничения доступа от ролевых моделей?

10. При каких условиях разрешима проблема безопасности для модели Харрисона-Руззо-Ульмана?

11. Приведите примеры информационных моделей? В чем их достоинства и недостатки?

12. Охарактеризуйте модели защиты автоматизированной системы от отказов в обслуживания.