ПРИБЛИЖЁННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
Вычисление интегралов встречается при моделировании достаточно часто. Численные методы обычно применяются при взятии неберущихся интегралов от достаточно сложных функций, которые предварительно табулируются, или при интегрировании таблично заданных функций, что в экономических приложениях встречается значительно чаще.
4.1. Концепция численного интегрирования
Все численные методы строятся на том, что подынтегральная функция приближенно заменяется более простой (горизонтальной или наклонной прямой, параболой 2-го, 3-го или более высокого порядка), от которой интеграл легко берется. В результате получаются формулы интегрирования, называемые квадратурными, в виде взвешенной суммы ординат подынтегральной функции в отдельных точках:
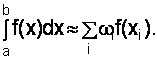 (4.1)
(4.1)
Чем меньше интервалы, на которых производят замену, тем точнее вычисляется интеграл. Поэтому исходный отрезок [а, b] для повышения точности делят на несколько равных или неравных интервалов, на каждом из которых применяют формулу интегрирования, а затем складывают результаты.
Все методы различаются значениями ординат xi, и весов i.
В большинстве случаев погрешность численного интегрирования определяется путем двойного интегрирования: с исходным шагом (шаг определяется путем равномерного деления отрезка (b–а) на число отрезков n:
h = (b–а)/n)и с шагом, увеличенным в 2 раза. Разница вычисленных значений интегралов определяет погрешность.
Сравнение эффективности различных методов проводится по степени полинома, который данным методом интегрируется точно, без ошибки. Чем выше степень такого полинома, тем выше точность метода, тем он эффективнее [4].
4.2. Метод прямоугольников
Метод прямоугольников можно отнести к простейшим методам.
В этом случае подынтегральная функция заменяется горизонтальной прямой (у = с0) со значением ординаты, т. е. значения функции соответственно слева или справа участка.
Вычисление определенного интеграла (геометрическая интерпретация определенного интеграла) – это вычисление площади криволинейной трапеции.
Существуют методы: левых прямоугольников, правых прямоугольников и средних прямоугольников [4].
Разбиваем отрезок [а, b] на n частей с равномерным шагом h.
Метод левых прямоугольников
Формулы интегрирования:
• для одного участка интегрирования (рис. 4.1, a):
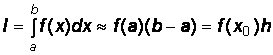 ; (4.2)
; (4.2)
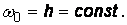 (4.3)
(4.3)
для n участков интегрирования (рис. 4.1, б):
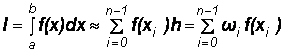 ; (4.4)
; (4.4)
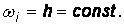 (4.5)
(4.5)
а 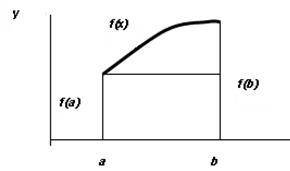
| б 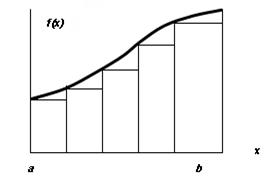
|
| Рис. 4.1. Иллюстрация метода левых прямоугольников: а – для одного участка интегрирования; б – для n участков интегрирования |
Метод правых прямоугольников
Формулы интегрирования:
• для одного участка интегрирования (рис. 4.2, a):
 ; (4.6)
; (4.6)
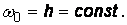 (4.7)
(4.7)
• для n участков интегрирования (рис. 4.2, б):
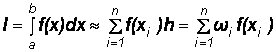 ; (4.8)
; (4.8)
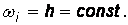 (4.9)
(4.9)
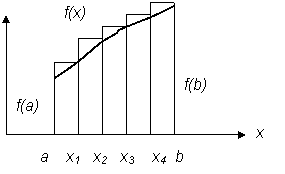 аб
аб
|
| ||||
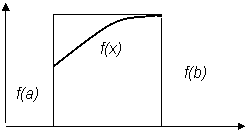
| |||||
Рис. 4.2. Иллюстрация метода правых прямоугольников:
a – для одного участка интегрирования; б – для n участков интегрирования
Метод средних прямоугольников
Формулы интегрирования:
• для одного участка интегрирования (рис. 4.3, a):
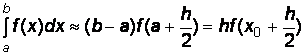 ; (4.10)
; (4.10)
• для n участков интегрирования (рис. 4.3, б):
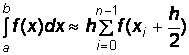 ; (4.11)
; (4.11)
где x0 = a, x1 = b, h = b–a.
| 
| |||
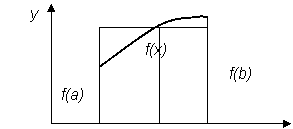
|
Нетрудно заметить, что в методе прямоугольников интеграл вычисляется абсолютно точно только при f(х) = с (соnst).
На рис. 4.4 для сравнения приведены примеры прямоугольников при различном числе участков. Наглядно видно, что площадь всех прямоугольников на правом рисунке отличается меньше от площади под кривой f(х), чем на левом.
Метод прямоугольников не находит практического применения в силу значительных погрешностей, что подтверждается рис. 4.4.
a б
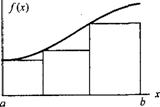
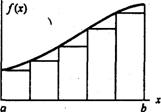
Рис. 4.4. Иллюстрация метода левых прямоугольников:
а – с 3 участками разбиения отрезка интегрирования [а, b];
б – с 6 участками разбиения отрезка интегрирования [а, b]
4.3. Метод трапеций
Метод трапеций так же, как и метод прямоугольников, относится к простейшим методам. В этом случае подынтегральная функция заменяется наклонной прямой (у = с1х + со) [2].
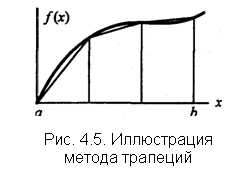 На рис. 4.5 приведен пример вычисления интеграла методом трапеций. По сравнению с методом прямоугольников метод трапеций более точен, так как трапеция точнее заменяет соответствующую криволинейную трапецию, чем прямоугольник.
На рис. 4.5 приведен пример вычисления интеграла методом трапеций. По сравнению с методом прямоугольников метод трапеций более точен, так как трапеция точнее заменяет соответствующую криволинейную трапецию, чем прямоугольник.
Нетрудно заметить, что в методе трапеций интеграл вычисляется абсолютно точно только при f(х) линейной или кусочно-линейной.
Формулы интегрирования:
• для одного участка интегрирования:
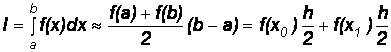 ; (4.12)
; (4.12)
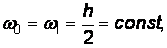 (4.13)
(4.13)
где x0 = a, x1 = b, h = b–a;
• для n участков интегрирования (рис. 4.5):
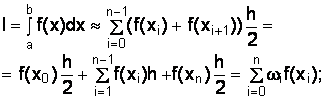 (4.14)
(4.14)
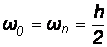 ; (4.15)
; (4.15)
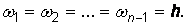 (4.16)
(4.16)
Погрешность R вычисления интеграла методом трапеций при использовании двойного просчета на практике может быть определена из следующего соотношения:
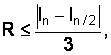 (4.17)
(4.17)
где In и In/2 – соответственно значения интеграла при числе разбиений n и n/2.
Существуют и аналитические выражения для определения погрешности, но они требуют знания второй производной подынтегральной функции, поэтому имеют только теоретическое значение. С использованием двойного просчета можно организовать автоматический подбор шага интегрирования (т. е. числа разбиений n) для обеспечения заданной погрешности интегрирования (последовательно удваивая шаг и контролируя погрешность).
Пример. 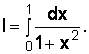
Вычислить для всего интервала и с делением интервала на четыре участка.
Решение.
Аналитическое вычисление данного интеграла дает I = агсtg(1)–агсtg(0) = = 0,7853981634. В нашем случае:
1)h = 1; xо = 0; x1 = 1;
2) h = 0,25 (1/4); x0 = 0; x1 = 0,25; x2 = 0,5; х3 = 0,75; x4 = 1; 
Вычислим методом левых прямоугольников:
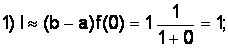
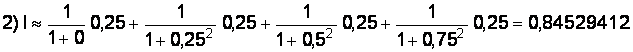
Вычислим методом правых прямоугольников:


Вычислим методом средних прямоугольников:
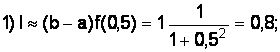
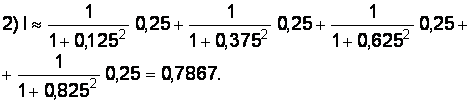
Вычислим методом трапеций:
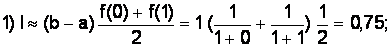
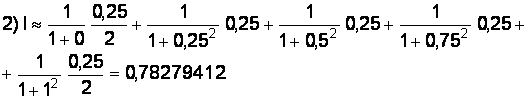
4.4. Метод Симпсона (парабол)
Этот метод базируется на замене подынтегральной функции квадратичной параболой, которая строится уже не по двум (как прямая в методе трапеций), а по трем точкам на каждом участке (поэтому число разбиений должно быть четным). По этим трем точкам (крайние точки участка и средняя точка) строится интерполяционная функция – полином второго порядка, который аналитически интегрируется [2]. Получается следующая расчетная формула:
• для одного участка интегрирования:
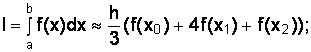 (4.18)
(4.18)
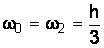 ; (4.19)
; (4.19)
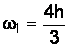 , (4.20)
, (4.20)
где x0 = a; x1 = (b–a)/2; x2 = b; h = (b–a)/2;
• для n участков интегрирования:
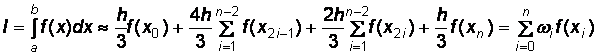 ; (4.21)
; (4.21)
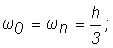 (4.22)
(4.22)
 ; (4.23)
; (4.23)
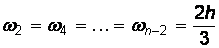 . (4.24)
. (4.24)
В формуле (4.24) все ординаты с нечетными номерами имеют коэффициент 4h/З, а с четными – 2h/3 (кроме нулевого и последнего). При работе с этим методом обязательно разбивают весь интервал на четное число участков.
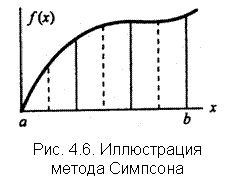
На рис. 4.6 приведен пример вычисления интеграла методом Симпсона. По сравнению с методами прямоугольников и трапеций он более точен, что наглядно видно из графика (подынтегральная функция почти совпадает с параболой).
 Метод Симпсона обеспечивает вычисление интеграла точно, без погрешности при полиноме третьего порядка. Следовательно, этот метод предпочтительнее предыдущих. Количественно оценить погрешность при использовании двойного просчета можно по соотношению
Метод Симпсона обеспечивает вычисление интеграла точно, без погрешности при полиноме третьего порядка. Следовательно, этот метод предпочтительнее предыдущих. Количественно оценить погрешность при использовании двойного просчета можно по соотношению
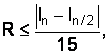 (4.25)
(4.25)
т. е. при увеличении числа разбиений в 2 раза погрешность падает в 15 раз.
Теоретические формулы оценки погрешности содержат производную четвертого порядка от подынтегральной функции, поэтому не имеют практического значения [2].
Пример
Рассмотрим вычисление интеграла из предыдущего раздела.
Решение
В случае одного участка будем иметь: x0 = 0, x1 = 0,5, х2 = 1, h = 0,5.
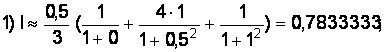
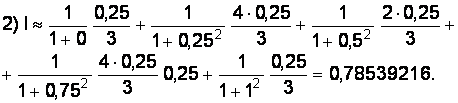
4.4. Пример решения задачи вычисления определенного
интеграла с использованием пакета Excel
Постановка задачи. Задан определенный интеграл 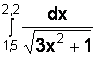 .
.
Определить приближенное значение интеграла методами прямоугольников, трапеций и Симпсона (парабол). Проинтегрировать аналитически и определить относительную погрешность вычислений.
Выполнение. Необходимо занести исходные данные в ячейки электронной таблицы:
| a = | 1,5 | |
| b = | 2,2 | |
| n = | ||
| h = | (2,2 – 1,5) / 20 = | 0,035. |
Вычислить точное значение определенного интеграла по формуле Ньютона–Лейбница.
Точное значение интеграла F(x)= 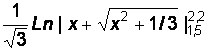 = 0,210529.
= 0,210529.
F(a) = 0,65456866; F(b) = 0,86509805; F(b)–F(a) = 0,210529.
Подготовить табл. 4.1 с данными, необходимыми для расчета определенного интеграла различными методами.
Таблица 4.1
Дата добавления: 2016-05-31; просмотров: 3387;











