Способы нормирования предела допускаемой основной погрешности
Способ выражения предела допускаемой основной погрешности определяется назначением СИ и характером изменения погрешности в пределах диапазона измерения. В общем случае зависимость погрешности от входного сигнала может быть произвольной. Но из всего многообразия СИ по характеру изменения погрешности в пределах диапазона измерения (или в пределах шкалы) можно выделить следующие основные группы:
• СИ, для которых преобладает аддитивная составляющая погрешности;
• СИ, для которых преобладает мультипликативная составляющая погрешности,
• СИ, для которых необходимо учитывать обе (аддитивную и мультипликативную) составляющие погрешности.
В группе СИ, для которых преобладает аддитивная составляющая погрешности, предел допускаемой абсолютной погрешности
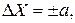 где
где 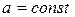 . (1.1)
. (1.1)
В ряде случаев оказывается удобно нормировать предел допускаемой абсолютной основной погрешности с использованием одного числового значения в соответствии с выражением (1.1) (например, для средств измерения линейных размеров — микрометры, штангенциркули и т. п.). Класс точности в этом случае принято обозначать путем указания числа а (например, для микрометра 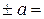 0,01мм) либо в виде условных обозначений, в качестве которых используют римские цифры или прописные буквы латинского алфавита. Причем классам точности, которым соответствуют меньшие пределы допускаемых погрешностей, должны соответствовать меньшие цифры или буквы, находящиеся ближе к началу алфавита.
0,01мм) либо в виде условных обозначений, в качестве которых используют римские цифры или прописные буквы латинского алфавита. Причем классам точности, которым соответствуют меньшие пределы допускаемых погрешностей, должны соответствовать меньшие цифры или буквы, находящиеся ближе к началу алфавита.
Однако для электроизмерительных приборов нормировать предел допускаемой основной погрешности путем указания одного числового значения в соответствии с выражением (1.1) оказалось не очень удобно, так как при этом трудно сравнивать приборы по точности, если они имеют разные диапазоны измерений или являются многопредельными. Для таких приборов более удобным оказалось нормировать предел допускаемой основной приведенной погрешности g и выражать его в процентах:
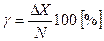 , (1.2)
, (1.2)
где N — нормирующее значение.
Нормирующее значение выбирается в зависимости от особенностей конкретного СИ. В соответствии с ГОСТ 8.401—80 нормирующее значение принимают равным:
1) конечному значению шкалы прибора Хк для СИ с равномерной шкалой, практически равномерной и степенной шкалой, если нулевая отметка находится на краю или вне шкалы (например, для амперметра со шкалой 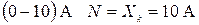 );
);
2) сумме конечных значений шкалы прибора (без учета знаков), если нулевая отметка находится внутри шкалы, например для миллиамперметра со шкалой (50-0-100)мА 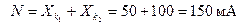 ;
;
3) номинальному значению измеряемой величины, если таковое установлено (например, для частотомера, предназначенного для контроля частоты питающей сети со шкалой 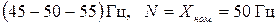 );
);
4) длине шкалы (выраженной в мм), если шкала имеет резко сужающиеся деления (логарифмические, гиперболические шкалы, как например, шкала омметра).
В последнем случае абсолютную погрешность и длину шкалы выражают в одних единицах (в мм).
Для приборов со шкалой, градуированной в единицах ФВ, для которой принята шкала с условным нулем (например, для приборов, измеряющих температуру в градусах Цельсия), нормирующее значение принимается равным разности конечного и начального значений шкалы, т. е. диапазону измерений 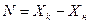 .
.
Приведенная погрешность СИ, определяемая в соответствии с формулой (1.2), может иметь любое значение. Но для того, чтобы упорядочить требования к СИ по точности и ограничить их номенклатуру, конкретное значение приведенной погрешности для присвоения СИ класса точности следует выбирать из ряда предпочтительных чисел, регламентированного ГОСТ 13600—68 (выбирается ближайшее число со стороны больших значений):
(1; 1,5; 2; 2,5; 4; 5; 6) *10n , где n = 1; 0; - 1; - 2; ...
Класс точности указывается в технической документации на СИ и в виде условного обозначения наносится на шкалу или корпус измерительного прибора. Если для СИ нормируется предел допускаемой основной приведенной погрешности в соответствии с формулой (1.2), то условное обозначение класса точности представляет собой само число g, выраженное в процентах (например, 0,5 или 2,0) во всех случаях, кроме тех, когда СИ имеет резко нелинейную шкалу. Для СИ с резко нелинейной шкалой (когда нормирующее значение N равно длине шкалы) условное обозначение класса точности имеет вид: 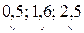 .
. 
В группе СИ, для которых преобладает мультипликативная составляющая погрешности, предел допускаемой абсолютной погрешности можно записать в следующем виде:
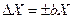 ,
,
где b — положительное число, не зависящее от X.
Переходя к относительным погрешностям, получаем, что предел допускаемой основной относительной погрешности для СИ этой группы:
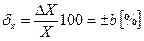 , где b = const. (1.3)
, где b = const. (1.3)
Для СИ этой группы числовое значение b, выраженное в процентах, выбирается из того же ряда предпочтительных чисел и указывается в технической документации в качестве класса точности. Условное обозначение класса точности на шкале или на корпусе прибора имеет вид, например,
 0,5
0,5
В группе СИ, для которых необходимо учитывать как аддитивную, так и мультипликативную составляющие погрешности, предел допускаемой абсолютной погрешности можно выразить в виде суммы двух членов:
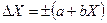 ,
,
где X— значение измеряемой величины;
а и b — положительные числа, не зависящие от X.
Предел допускаемой основной погрешности для приборов этой группы нормируется по величине приведенной погрешности. Нормирующей величиной является конечное значение шкалы Хк, но приведенная погрешность определяется в двух точках шкалы: при Х=0 (начальная отметка шкалы) и при Х= Хк (конечная отметка шкалы).
Приведенная погрешность для любой точки шкалы (в процентах):
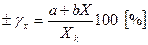 , (1.4)
, (1.4)
при 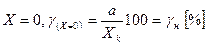 ,
,
при 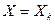 ,
, 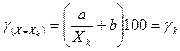
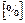 ,
,
где gн — приведенная погрешность в начале шкалы;
gк — приведенная погрешность в конце шкалы.
Числовые значения gн и gк, выраженные в процентах, выбираются из ряда чисел, регламентированных ГОСТом, и приводятся в технической документации в качестве класса точности СИ, имеющего аддитивную и мультипликативную составляющие погрешности. Условное обозначение класса точности на шкале или на корпусе прибора имеет вид дроби gк /gн (например, 0.5/0.2).
Для средств измерения этой группы предел допускаемой основной абсолютной и предел допускаемой основной относительной погрешностей можно записать, используя формулы (1.4):
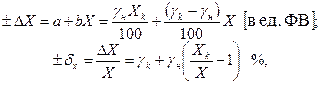 (1.5)
(1.5)
где Хк — используемый предел измерения;
X — результат измерения (отсчет по шкале).
Условные обозначения классов точности и формулы для расчета погрешностей результата измерений сведены в таблицу 1.
Рассмотренные способы нормирования предела допускаемой основной погрешности наиболее часто используются для средств электрических измерений, но не исчерпывают всех возможных вариантов нормирования предела допускаемой основной погрешности. В обоснованных случаях ГОСТ разрешает устанавливать предел допускаемой основной погрешности по более сложной формуле или в виде таблицы или графика.
Пределы допускаемых дополнительных погрешностей нормируются путем указания их связи с пределом допускаемой основной погрешности.
Классы точности электроизмерительных приборов Таблица 1
| Характер погреш-ности | Форма выражения класса точности СИ | Предел допуска-емой погреш-ности | Обоз-наче-ние класса | Погрешность результата измерений | |
| Абсолютная | Относительная | ||||
| Аддитивная погрешность | Приведенная погрешность в %. Нормирующее значение – N выражено в единицах измеряемой ФВ. | 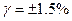
|
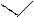 1.5 1.5
| 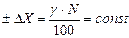
| 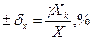
|
| Приведенная погреш-ность в %. Нормирующее значение принято равным геометрической длине шкалы – L[мм] | 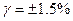
| 1.5 | 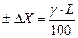 [в долях шкалы], [в долях шкалы],
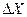 [в ед. ФВ]
надо определять в конкретной точке
шкалы [в ед. ФВ]
надо определять в конкретной точке
шкалы
| 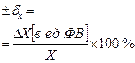
| |
| Мульти-плика-тивная погреш. | Относительная погрешность в %. |   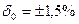
|  1.5
1.5
| 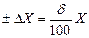
| 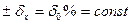
|
| Аддитивная+ Мультипликативная составляющие | Приведенная погреш-ность в двух точках шкалы, при Х=0 и Х=Хk. Нормирующее значение выражено в единицах измеряемой ФВ. |
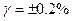 (при Х=0)
(при Х=0)
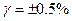 (при Х=Хk)
(при Х=Хk)
| 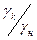
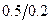
| 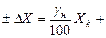
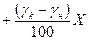
|
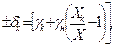 (%) (%)
|
Таким образом, класс точности СИ позволяет оценить как допускаемые пределы основной погрешности, так и допускаемые пределы всех дополнительных погрешностей по отдельности, соответствующие рабочим условиям эксплуатации СИ. При этом как основная погрешностьСИ, так и все дополнительные погрешности оцениваются в виде границ.
При определении границ общей погрешности результата для рабочих условий эксплуатации СИ суммировать основную и все дополнительные погрешности следует при заданной доверительной вероятности по формуле:
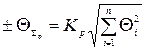 , (1.6)
, (1.6)
где 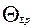 - суммарная доверительная граница не исключённых остатков составляющих систематической погрешности;
- суммарная доверительная граница не исключённых остатков составляющих систематической погрешности;
P - доверительная вероятность,
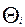 - граница i - ой составляющей.
- граница i - ой составляющей.
Коэффициент КP в общем случае зависит от доверительной вероятности Рдов и от числа суммируемых составляющих n. Строгое определение значения коэффициента КР достаточно сложная задача, поэтому на практике для обработки результатов технических измерений пользуются усредненными значениями коэффициента КP (не зависящими уже от числа слагаемых n).
Усредненные значения коэффициента КР приведены ниже [3,4]:
Рдов .......... 0,9 0,95 0,98 0,99
КР........... 0,95 1,1 1,3 1,4
При малом числе составляющих после нахождения 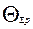 по формуле (6), необходимо сравнить ее с арифметической границей
по формуле (6), необходимо сравнить ее с арифметической границей 
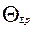 * =
* = 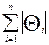 . Очевидно, что
. Очевидно, что 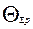 не может быть больше
не может быть больше 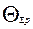 *.
*.
Если 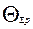 >
> 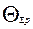 *, то в качестве границ суммарной систематической погрешности принимается меньшая величина, т. е.
*, то в качестве границ суммарной систематической погрешности принимается меньшая величина, т. е. 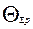 *.
*.
Для однозначных мер электрического сопротивления, емкости и индуктивности класса 0,02 и ниже число, обозначающее класс точности, - допускаемое отклонение действительного значения меры от номинального значения, указанного на мере, в процентах. Для однозначных мер электрического сопротивления класса 0,01 и выше число, обозначающее класс точности, равно допускаемому изменению сопротивления за год, выраженному в процентах.
В заключение следует подчеркнуть следующее. Класс точности СИ не является непосредственной характеристикой точности проведенных с помощью него измерений, но класс точности позволяет оценить (рассчитать) погрешность полученного результата. Класс точности является обобщенной характеристикой точности данного типа (вида) СИ, а не конкретного образца. Допускаемый предел основной погрешности есть предел суммы систематической и случайной составляющих погрешности СИ, но поскольку в техническом описании, как правило, отсутствуют сведения о виде закона распределения случайной составляющей погрешности, принято (если нет других оснований) считать распределение основной погрешности приборов данного типа (а, следовательно, и всех дополнительных погрешностей) в пределах указанных границ равномерным.
Основную погрешность можно считать систематической только в том случае, если для конкретного образца СИ данного вида по результатам поверки составлены поправочные таблицы или графики, позволяющие учесть систематическую погрешность.
Однократные измерения возможны при следующих условиях. Объем априорной информации об объекте должен быть таким, чтобы модель объекта и определение измеряемой ФВ не вызывали никаких сомнений. Методические погрешности должны быть либо заранее устранены, либо должно быть известно, как оценить их величину. Применяемые СИ должны быть исправными, а их метрологические характеристики должны соответствовать установленным нормам (СИ прошли периодическую поверку).
В зависимости от метода оценивания погрешностей прямых однократных измерений различают измерения с приближенным оцениванием погрешностей и измерения с точным оцениванием погрешностей. И в том и в другом случаях погрешность результата определяется расчетным путем с использованием метрологических характеристик используемого СИ, но в первом случае используются типовые метрологические характеристики (метрологические характеристики типа СИ), приводимые в техническом описании, а во втором случае используются индивидуальные метрологические характеристики конкретного (используемого) образца СИ, которые предварительно определяются путем поверки и дополнительных исследований свойств этого образца СИ.
Дата добавления: 2020-10-14; просмотров: 1152;











