Анализ систем, имеющих автоматическое регулирование.
Исследование регулируемой системы имеет два аспекта: анализ и синтез. Решение задачи анализа предполагает проверку устойчивости системы, выявление вида переходного процесса и определение его качества при известных параметрах регулирующих устройств и системы. Задачи синтеза сводятся к определению вида регулятора (структурной схемы системы регулирования) и его параметров, исходя из требований к устойчивости и качеству переходного процесса регулируемой системы.
На примере простой системы (станция — шины неизменного напряжения) рассмотрим основные физические представления, не выделяя задач анализа и синтеза. Генераторы без демпферных обмоток снабжены автоматическим регулятором возбуждения (АРВ) без запаздывания 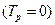 . При наличии регулятора, реагирующего на отклонение напряжения (коэффициент усиления
. При наличии регулятора, реагирующего на отклонение напряжения (коэффициент усиления 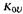 ), имеем уравнения
), имеем уравнения
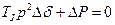
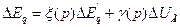 ,
,
причем 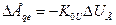 ;
; 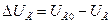 ;
; 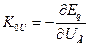 ;
;
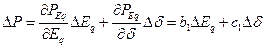 ;
;
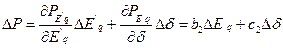 ;
;
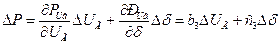 .
.
Входящие в эти уравнения коэффициенты 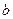 и с зависят от режима. Система уравнений путем преобразований может быть сведена к трем уравнениям с неизвестными
и с зависят от режима. Система уравнений путем преобразований может быть сведена к трем уравнениям с неизвестными 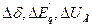 :
:
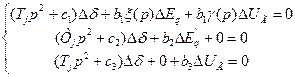
Определитель системы
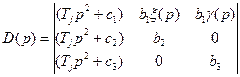 .
.
Раскрыв выражение для главного определителя системы и приравняв его к нулю, получим:
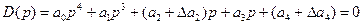 , где
, где
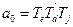 ;
;  ;
;  ;
;  ;
; 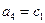 .
.
Через 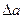 обозначены составляющие коэффициентов а, зависящие от действия регулятора:
обозначены составляющие коэффициентов а, зависящие от действия регулятора:
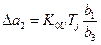 ;
;
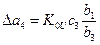 ;
;
 .
.
Анализ устойчивости, выполненный по способу Гурвица, дает возможность установить неравенства, при выполнении которых обеспечивается статическая устойчивость системы:
1) 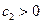 ;
;
2) 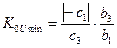 ;
;
3) 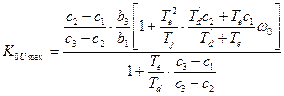
 .
.
Дата добавления: 2020-10-14; просмотров: 758;











